用 Python 实现粒子群算法

作者简介：Boblee，人工智能硕士毕业，擅长及爱好Python，基于Python研究人工智能、群体智能、区块链等技术，并使用Python开发前后端、爬虫等。

一、粒子群算法介绍

1、初始化

首先，我们设置最大迭代次数，目标函数的自变量个数，粒子的最大速度，位置信息为整个搜索空间，我们在速度区间和搜索空间上随机初始化速度和位置，设置粒子群规模为M，每个粒子随机初始化一个飞翔速度。

2、个体极值与全局最优解

定义适应度函数，个体极值为每个粒子找到的最优解，从这些最优解找到一个全局值，叫做本次全局最优解。与历史全局最优比较，进行更新。

3、更新速度和位置的公式

节选自 https://blog.csdn.net/weixin_40679412/article/details/80571854

二、算法实现

1、初始化粒子，计算适应度值

初始化粒子x及速度v，并调用适应度函数计算适应度值。并选出最小适应度值及对应的x值。

x = []
v = []
for j in range(self.N):
    x.append([random.random() for i in range(self.dim)])
    v.append([random.random() for m in range(self.dim)])
fitness = [self.fun(x[j]) for j in range(self.N)]
p = x
best = min(fitness)
pg = x[fitness.index(min(fitness))]

2、更新粒子位置，计算新适应度值

根据1中公式更新粒子位置及速度，并调用适应度函数计算适应度值。

for t in range(self.T):
    for j in range(self.N):
        for m in range(self.dim):
            v[j][m] = self.w * v[j][m] + self.c1 * random.random() * (
                    p[j][m] - x[j][m]) + self.c2 * random.random() * (pg[m] - x[j][m])
    for j in range(self.N):
        for m in range(self.dim):
            x[j][m] = x[j][m] + v[j][m]
            if x[j][m] > self.x_bound[1]:
                x[j][m] = self.x_bound[1]
            if x[j][m] < self.x_bound[0]:
                x[j][m] = self.x_bound[0]
    fitness_ = []
    for j in range(self.N):
        fitness_.append(self.fun(x[j]))

3、更新粒子全局最优解

如果新计算出的适应度值比前期计算的适应度值小，则更新粒子全局最优解。

if min(fitness_) < best:
    pg = x[fitness_.index(min(fitness_))]
    best = min(fitness_)

4、整体代码

其中T为迭代次数，x_bound为粒子范围，w、c1、c2为公式参数，dim为粒子维度，N为每次迭代粒子总数。fun函数根据需要自己修改。

import random
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']  # 步骤一（替换sans-serif字体）
plt.rcParams['axes.unicode_minus'] = False


class PSO(object):
    def __init__(self):
        self.x_bound = [-1, 1]
        self.T = 100
        self.w = 0.15
        self.N = 10000
        self.dim = 20
        self.c1 = 1.5
        self.c2 = 1.5

    def fun(self, x):
        result = 0
        for i in x:
            result = result + pow(i, 2)
        return result

    def pso_main(self):
        x = []
        v = []
        for j in range(self.N):
            x.append([random.random() for i in range(self.dim)])
            v.append([random.random() for m in range(self.dim)])
        fitness = [self.fun(x[j]) for j in range(self.N)]
        p = x
        best = min(fitness)
        pg = x[fitness.index(min(fitness))]
        best_all = []
        for t in range(self.T):
            for j in range(self.N):
                for m in range(self.dim):
                    v[j][m] = self.w * v[j][m] + self.c1 * random.random() * (
                            p[j][m] - x[j][m]) + self.c2 * random.random() * (pg[m] - x[j][m])
            for j in range(self.N):
                for m in range(self.dim):
                    x[j][m] = x[j][m] + v[j][m]
                    if x[j][m] > self.x_bound[1]:
                        x[j][m] = self.x_bound[1]
                    if x[j][m] < self.x_bound[0]:
                        x[j][m] = self.x_bound[0]
            fitness_ = []
            for j in range(self.N):
                fitness_.append(self.fun(x[j]))
            if min(fitness_) < best:
                pg = x[fitness_.index(min(fitness_))]
                best = min(fitness_)
            best_all.append(best)
            print('第' + str(t) + '次迭代：最优解位置在' + str(pg) + '，最优解的适应度值为：' + str(best))
        plt.plot([t for t in range(self.T)], best_all)
        plt.ylabel('适应度值')
        plt.xlabel('迭代次数')
        plt.title('粒子群适应度趋势')
        plt.show()

三、实验操作

本文选取一个适应度函数作为实验对象：

X可以选取不同的值，比如X=5：

理论上在上述范围内，其函数最小值为：

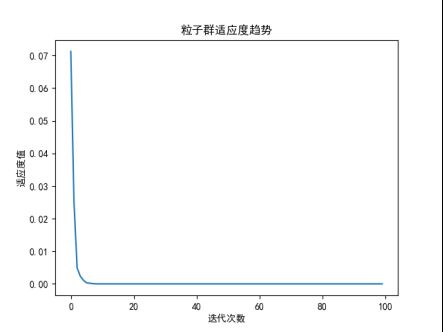
使用粒子群优化时N=1000，其它参数默认。其适应度函数值如下图所示。

可以看出来在迭代几次后适应度值回归0，可以看出粒子群还是很强大的。最终结果：第99次迭代：最优解位置在[-0.0033824972144645693, -0.00041073819884876104, -0.020837825233968172, -0.004563775182149339, -0.0014281389517050655]，最优解的适应度值为：8.442317543610645e-06，可以看出最终结果都接近0，还是强大。

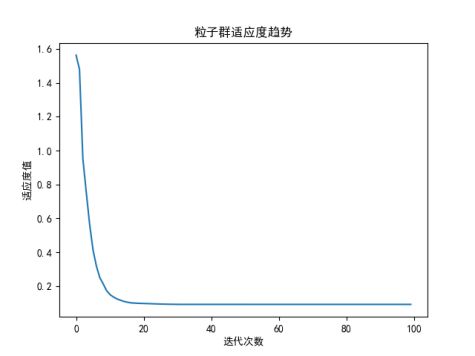
最后模拟实验了一把x=20，一直没收敛，最终把w改为0.15，才快速收敛，看来还是要调参。

最终结果：第99次迭代：最优解位置在[0.2116144935400703, 0.07887187671813765, -1.3609859231410183e-08, -1.799398730028292e-07, -0.11696106146417741, 0.10037271577264674, -0.017925057083705564, -0.02802360488939756, -0.005706816942171255, -0.013489326069795754, 0.05147854918903612, 0.0812079535495765, -0.014420970040807935, 6.384991604874465e-05, 0.00505764782058281, -0.01506357441766914, 0.0011273641957984912, 0.07792954674542905, -0.0015019673080418508, 0.022567192289875606]，最优解的适应度值为：0.09236825011895983

往期精彩

超简单！基于Python搭建个人“云盘”

推荐一些能提高生产力的 Python 库

Excel VS Python 谁更适合数据分析？

硬核！30 张图解 HTTP 常见的面试题

谷歌Python代码风格指南,翻译版来了！

python每日更换“必应图片”为“桌面壁纸”

教你使用Python下载全网视频！

END

关注【程序IT圈】，更多的Python好文输出