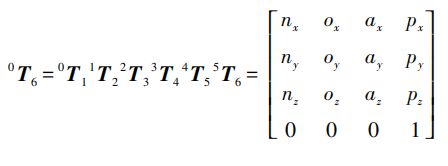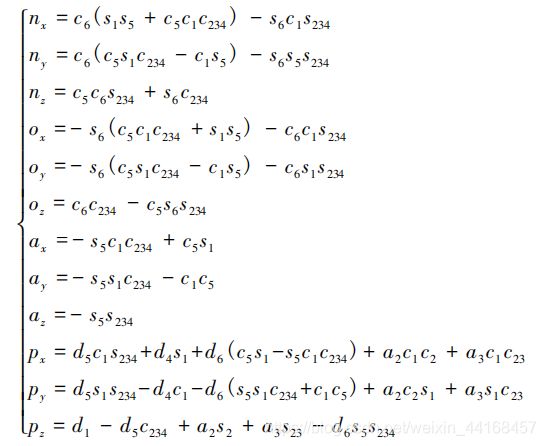04轨迹规划基础----正逆运动学的C++代码编写

1.摘要

文章的主要内容是,编写C++代码，实现六轴机械臂的正运动学运算（输入为关节角度，输出为T6 ）和逆运动学求解（输入为T6，输出为关节角度），这个代码是很基础的，可能十几年前网上就有成熟的了，当然你也可以用我下边粘贴的代码。
本文数学公式截图来自论文

[1]张付祥,赵阳.UR5机器人运动学及奇异性分析[J].河北科技大学学报,2019,40(01):51-59.

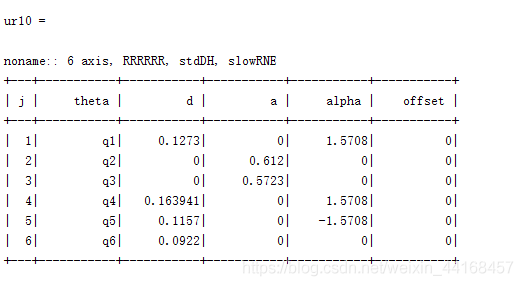
2.DH参数表

DH参数表基于ur10机器人

3.正运动学

①数学公式


②

#include
using namespace  std;
const double d1 = 0.1273;
const double a2 = 0.612;
const double a3 = 0.5723;
const double d4 = 0.163941;
const double d5 = 0.1157;
const double d6 = 0.0922;
const double ZERO_THRESH = 0.00000001;
int SIGN(double x)
{
    return (x > 0) - (x < 0);
}
const double PI = 3.1415926;
void forward(const double* q, double* T) {
    double s1 = sin(*q), c1 = cos(*q); q++;
    double q23 = *q, q234 = *q, s2 = sin(*q), c2 = cos(*q); q++;
    double s3 = sin(*q), c3 = cos(*q); q23 += *q; q234 += *q; q++;
    double s4 = sin(*q), c4 = cos(*q); q234 += *q; q++;
    double s5 = sin(*q), c5 = cos(*q); q++;
    double s6 = sin(*q), c6 = cos(*q);
    double s23 = sin(q23), c23 = cos(q23);
    double s234 = sin(q234), c234 = cos(q234);
   
    *T = c6 * (s1 * s5 + c234 * c1 * c5) - s234 * c1 * s6; T++;  //nx
    *T = -s6 * (s1 * s5 + c234 * c1 * c5) - s234 * c1 * c6; T++;  //Ox
    *T =-( c234 * c1 * s5 - c5 * s1); T++;//ax
    *T =- (d6 * c234 * c1 * s5 - a3 * c23 * c1 - a2 * c1 * c2 - d6 * c5 * s1 - d5 * s234 * c1 - d4 * s1); T++;//Px
    
    *T = -c6 * (c1 * s5 - c234 * c5 * s1) - s234 * s1 * s6; T++;//ny
    *T = s6 * (c1 * s5 - c234 * c5 * s1) - s234 * c6 * s1; T++;//Oy
    *T = -(c1 * c5 + c234 * s1 * s5); T++;//ay
    *T = -(d6 * (c1 * c5 + c234 * s1 * s5) + d4 * c1 - a3 * c23 * s1 - a2 * c2 * s1 - d5 * s234 * s1); T++;//py
    
    
    *T = -(-c234 * s6 - s234 * c5 * c6); T++;//nz
    *T = -(s234 * c5 * s6 - c234 * c6); T++;//oz
    *T = -s234 * s5; T++;//az
    *T = d1 + a3 * s23 + a2 * s2 - d5 * (c23 * c4 - s23 * s4) - d6 * s5 * (c23 * s4 + s23 * c4); T++;//Pz
    *T = 0.0; T++; *T = 0.0; T++; *T = 0.0; T++; *T = 1.0;//姿态
}

int main()
{
    double Q[6] = { 0.1, 0.2, 0.3, 0.4, 0.5, 0.6 };
    double t[4][4];
    double * T,*q;
    q = &Q[0];
    T = &t[0][0]; 
    forward(q, T);
    //输出q
    cout << "关节角度q:   " << "["  ;
    for (int i = 0; i < 6; i++) {cout << Q[i]<<"  ";}
    cout << "]"<<endl;    
    //输出JZ
    cout << "矩阵T:   " <<endl ;
    for (int i = 0; i < 4; i++) 
    { 
        for (int j = 0; j < 4; j++)
        {
            cout <<t[i][j]<<"      ";        }
        cout << endl;
    }
    return 0;
    }

运行结果：

关节角度q:   [0.1  0.2  0.3  0.4  0.5  0.6  ]
矩阵T:
0.0473957      -0.976785      -0.208915      1.18382
-0.392918      0.174058      -0.90295      -0.127305
0.918351      0.124882      -0.375547      0.416715
0      0      0      1

4.逆运动学

这个我应该码出来的，但是我家好冷，我的手已经僵了，我现在感觉我敲机械键盘像是敲缝纫机，所以我明天会将这个文章更新（PS：我写的逆运动学代码，肯定会比matlab自带的好用哦！）

好久没更新的，我今天上号我发现我多了几个粉丝！啊我好激动，我的动力来了！！！！
以下为逆运动学计算代码
①数学公式




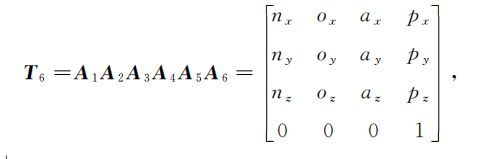
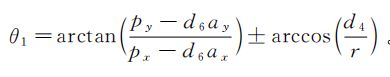
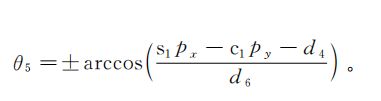
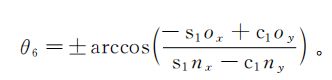
接下求第2、3、4关节的时候有点复杂了，你可要看好了

#include
using namespace  std;
const double d1 = 0.1273;
const double a2 = 0.612;
const double a3 = 0.5723;
const double d4 = 0.163941;
const double d5 = 0.1157;
const double d6 = 0.0922;
const double ZERO_THRESH = 0.00000001;
int SIGN(double x)
{
    return (x > 0) - (x < 0);
}
const double PI = 3.1415926;
void forward(const double* q, double* T) {
    double s1 = sin(*q), c1 = cos(*q); q++;
    double q23 = *q, q234 = *q, s2 = sin(*q), c2 = cos(*q); q++;
    double s3 = sin(*q), c3 = cos(*q); q23 += *q; q234 += *q; q++;
    double s4 = sin(*q), c4 = cos(*q); q234 += *q; q++;
    double s5 = sin(*q), c5 = cos(*q); q++;
    double s6 = sin(*q), c6 = cos(*q);
    double s23 = sin(q23), c23 = cos(q23);
    double s234 = sin(q234), c234 = cos(q234);
   
    *T = c6 * (s1 * s5 + c234 * c1 * c5) - s234 * c1 * s6; T++;  //nx
    *T = -s6 * (s1 * s5 + c234 * c1 * c5) - s234 * c1 * c6; T++;  //Ox
    *T =-( c234 * c1 * s5 - c5 * s1); T++;//ax
    *T =- (d6 * c234 * c1 * s5 - a3 * c23 * c1 - a2 * c1 * c2 - d6 * c5 * s1 - d5 * s234 * c1 - d4 * s1); T++;//Px
    
    *T = -c6 * (c1 * s5 - c234 * c5 * s1) - s234 * s1 * s6; T++;//ny
    *T = s6 * (c1 * s5 - c234 * c5 * s1) - s234 * c6 * s1; T++;//Oy
    *T = -(c1 * c5 + c234 * s1 * s5); T++;//ay
    *T = -(d6 * (c1 * c5 + c234 * s1 * s5) + d4 * c1 - a3 * c23 * s1 - a2 * c2 * s1 - d5 * s234 * s1); T++;//py
    
    
    *T = -(-c234 * s6 - s234 * c5 * c6); T++;//nz
    *T = -(s234 * c5 * s6 - c234 * c6); T++;//oz
    *T = -s234 * s5; T++;//az
    *T = d1 + a3 * s23 + a2 * s2 - d5 * (c23 * c4 - s23 * s4) - d6 * s5 * (c23 * s4 + s23 * c4); T++;//Pz
    *T = 0.0; T++; *T = 0.0; T++; *T = 0.0; T++; *T = 1.0;//姿态
}
int inverse(const double* T, double* q_sols,double * q) {
    int num_sols = 0;
    double T00 = *T; T++; double T01 = *T; T++; double T02 = *T; T++; double T03 = *T; T++;
    double T10 = *T; T++; double T11 = *T; T++; double T12 = *T; T++; double T13 = *T; T++;
    double T20 = *T; T++; double T21 = *T; T++; double T22 = *T; T++; double T23 = *T;
    double qq1, qq2, qq3, qq4, qq5, qq6;

    
    double q1[2];
    {
        double A = d6 * T12 - T13;
        double B = d6 * T02 - T03;
        double R = A * A + B * B;
        if (fabs(A) < ZERO_THRESH) {
            double div;
            if (fabs(fabs(d4) - fabs(B)) < ZERO_THRESH)
                div = -SIGN(d4) * SIGN(B);
            else
                div = -d4 / B;
            double arcsin = asin(div);
            if (fabs(arcsin) < ZERO_THRESH)
                arcsin = 0.0;
            if (arcsin < 0.0)
                q1[0] = arcsin + 2.0 * PI;
            else
                q1[0] = arcsin;
            q1[1] = PI - arcsin;
        }
        else if (fabs(B) < ZERO_THRESH) {
            double div;
            if (fabs(fabs(d4) - fabs(A)) < ZERO_THRESH)
                div = SIGN(d4) * SIGN(A);
            else
                div = d4 / A;
            double arccos = acos(div);
            q1[0] = arccos;
            q1[1] = 2.0 * PI - arccos;
        }
        else if (d4 * d4 > R) {
            return num_sols;
        }
        else {
            double arccos = acos(d4 / sqrt(R));
            double arctan = atan2(-B, A);
            double pos = arccos + arctan;
            double neg = -arccos + arctan;
            if (fabs(pos) < ZERO_THRESH)
                pos = 0.0;
            if (fabs(neg) < ZERO_THRESH)
                neg = 0.0;
            if (pos >= 0.0)
                q1[0] = pos;
            else
                q1[0] = 2.0 * PI + pos;
            if (neg >= 0.0)
                q1[1] = neg;
            else
                q1[1] = 2.0 * PI + neg;
        }
     
        qq1 = q1[1];
    }
    
    double q5[2][2];
    {
        for (int i = 0; i < 2; i++) {
            double numer = (T03 * sin(q1[i]) - T13 * cos(q1[i]) - d4);
            double div;
            if (fabs(fabs(numer) - fabs(d6)) < ZERO_THRESH)
                div = SIGN(numer) * SIGN(d6);
            else
                div = numer / d6;
            double arccos = acos(div);
            q5[i][0] = arccos;
            q5[i][1] = 2.0 * PI - arccos;
        }
        
        qq5 = q5[1][0];
    }
    
    {
        for (int i = 0; i < 2; i++) {
            for (int j = 0; j < 2; j++) {
                double c1 = cos(q1[i]), s1 = sin(q1[i]);
                double c5 = cos(q5[i][j]), s5 = sin(q5[i][j]);
                double q6;
                
                if (fabs(s5) < ZERO_THRESH)
                    q6 = 0;
                else {
                    q6 = atan2(SIGN(s5) * -(T01 * s1 - T11 * c1),
                        SIGN(s5) * (T00 * s1 - T10 * c1));
                    if (fabs(q6) < ZERO_THRESH)
                        q6 = 0.0;
                    if (q6 < 0.0)
                        q6 += 2.0 * PI;
                }
                double q2[2], q3[2], q4[2];

                double c6 = cos(q6), s6 = sin(q6);
                double x04x = -s5 * (T02 * c1 + T12 * s1) - c5 * (s6 * (T01 * c1 + T11 * s1) - c6 * (T00 * c1 + T10 * s1));
                double x04y = c5 * (T20 * c6 - T21 * s6) - T22 * s5;
                double p13x = d5 * (s6 * (T00 * c1 + T10 * s1) + c6 * (T01 * c1 + T11 * s1)) - d6 * (T02 * c1 + T12 * s1) +
                    T03 * c1 + T13 * s1;
                double p13y = T23 - d1 - d6 * T22 + d5 * (T21 * c6 + T20 * s6);

                double c3 = (p13x * p13x + p13y * p13y - a2 * a2 - a3 * a3) / (2.0 * a2 * a3);
                if (fabs(fabs(c3) - 1.0) < ZERO_THRESH)
                    c3 = SIGN(c3);
                else if (fabs(c3) > 1.0) {
                    // TODO NO SOLUTION
                    continue;
                }
                double arccos = acos(c3);
                q3[0] = arccos;
                q3[1] = 2.0 * PI - arccos;
                double denom = a2 * a2 + a3 * a3 + 2 * a2 * a3 * c3;
                double s3 = sin(arccos);
                double A = (a2 + a3 * c3), B = a3 * s3;
                q2[0] = atan2((A * p13y - B * p13x) / denom, (A * p13x + B * p13y) / denom);
                q2[1] = atan2((A * p13y + B * p13x) / denom, (A * p13x - B * p13y) / denom);
                double c23_0 = cos(q2[0] + q3[0]);
                double s23_0 = sin(q2[0] + q3[0]);
                double c23_1 = cos(q2[1] + q3[1]);
                double s23_1 = sin(q2[1] + q3[1]);
                q4[0] = atan2(c23_0 * x04y - s23_0 * x04x, x04x * c23_0 + x04y * s23_0);
                q4[1] = atan2(c23_1 * x04y - s23_1 * x04x, x04x * c23_1 + x04y * s23_1);
                qq6 = q6;
                qq2 = q2[0];
                qq3 = q3[0];
                qq4 = q4[0];
                num_sols++;
                }

            }
        }
    }
    *q = qq1; q++; *q = qq2; q++; *q = qq3; q++; *q = qq4; q++; *q = qq5; q++; *q = qq6; 

    return num_sols;
}

int main()
{
    double Q[6] = { 1, 0.2, 0.3, 0.4, 0.5, 0.8 };
    double t[4][4];
    double Qs[6] = { 0, 0, 0, 0, 0, 0 };
    double * T,*q,*qq;
    q = &Q[0];
    T = &t[0][0];  
    qq = &Qs[0];
    double q_sols[48];
    int num_sols;
    //逆运动学    
    forward(q, T);
    //输出初始的关节角度q
    cout << "输出初始的关节角度q:   " << "["  ;
    for (int i = 0; i < 6; i++) {cout << Q[i]<<"  ";}
    cout << "]"<<endl;    
    //输出由q 进行正运动学结果T
    cout << "输出由q 进行正运动学结果T:   " <<endl ;
    for (int i = 0; i < 4; i++) 
    { 
        for (int j = 0; j < 4; j++) 
        {
            cout <<t[i][j]<<"      ";
        }
        cout << endl;

    }
    num_sols = inverse(T, q_sols, qq);
    //输出由T输入 进行逆运动学得到的结果qq
    cout << "输出由T输入 进行逆运动学得到的结果qq:   " << "[";
    for (int i = 0; i < 6; i++) { cout << Qs[i] << "  "; }
    cout << "]" << endl;
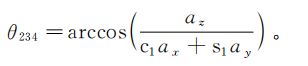
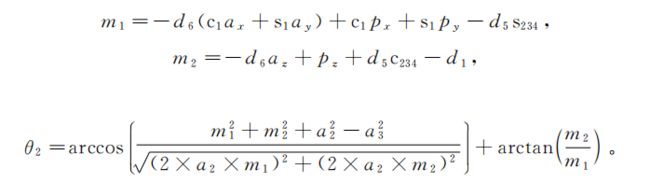
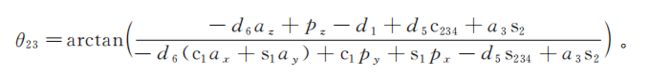
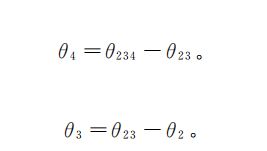
    return 0;
}

结果：

输出初始的关节角度q:   [1  0.2  0.3  0.4  0.5  0.8  ]
输出由q 进行正运动学结果T:
0.182807      -0.795703      0.577442      0.835595
-0.333502      -0.602703      -0.724931      0.848183
0.924856      -0.0600552      -0.375547      0.416715
0      0      0      1
输出由T输入 进行逆运动学得到的结果qq:   [1  0.2  0.3  0.4  0.5  0.8  ]

5预告

下一篇应该在明天或者后天：关于插值的c++代码/c++中姿态的图像表述
（先后顺序还没想好）
这篇文写了两天，所以中间有很多碎碎叨叨的话，我就不删了哦，代码运行有问题可以私戳我
我写的好认真，然后我发现有粉丝好开心，所以我就过分的设置成仅粉丝可见了，原谅我的虚荣，我的指针用的还不太熟，所以代码不够高级，请见谅~