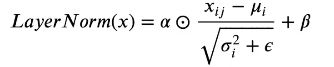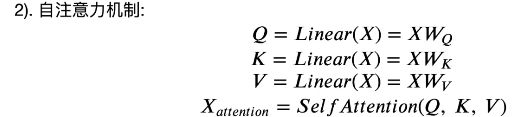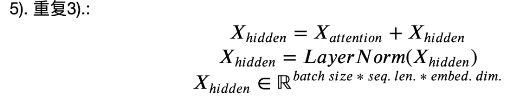Transformer理解

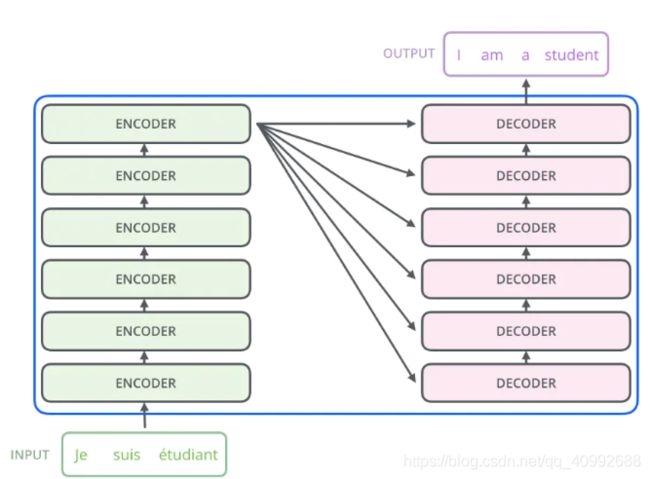
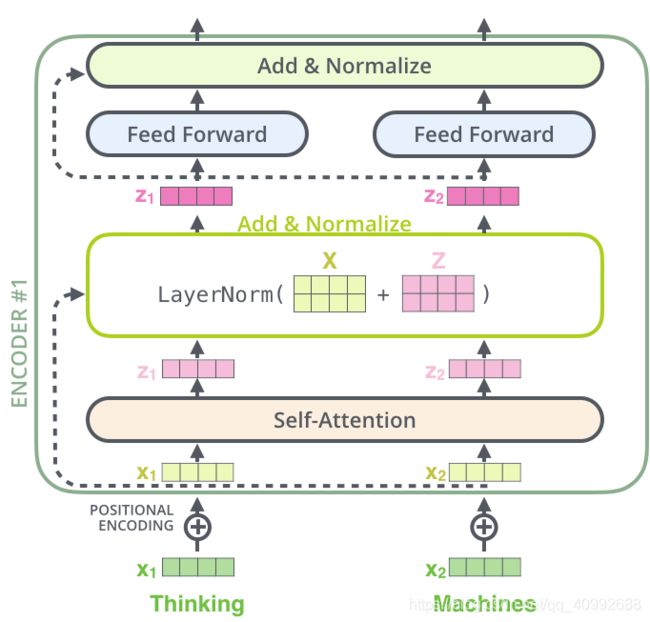
1.Transformer示意图

transformer宏观上由左边的六层endocer和右边的六层encoder构成，这些block各不分享权重，在左侧的encoder部分，前一时刻的encoder输出作为下一时刻encoder的输入，直到最后时刻的encoder的输出向量会传递给decoder的每一个block（block中的encoder-decoder attention模块）作为其输入的一部分。

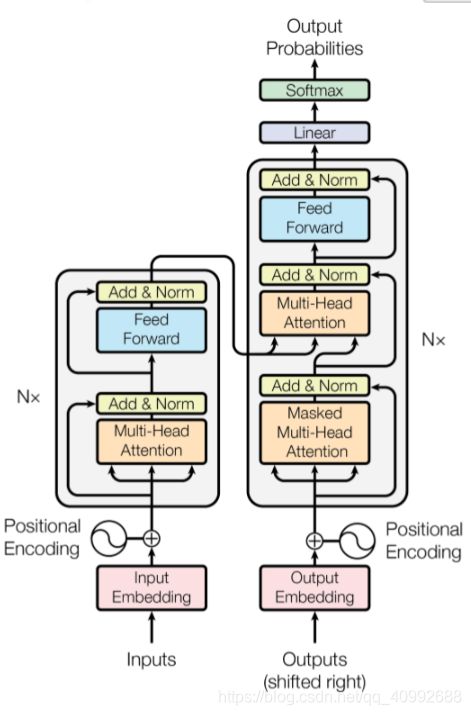
下图所示的是encoder和decoder的详细释义图：

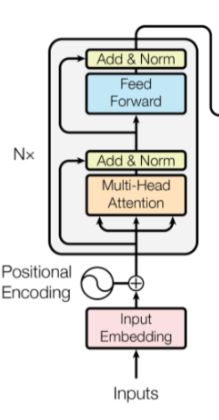
我们先来看一下encoder部分：

encoder主要由以下5部分构成：

①输入embedding

②positional encodeing位置编码

③multi-head attention多头注意力

④add and layer normalization 残差连接和层正则化

⑤feedforward前馈神经网络

下面我们一个一个解读：

①输入embedding：

首先，我们的输入的X维度为(batch_size, sequence_length)[batch大小，每句话的长度],

其中batch_size的设定目的是为了我们一次可以训练多句话，而我们初始的输入每句话一般都是由单词对应字典中的索引下标组成，通过初始的embedding，我们可以直接根据索引找到对应的行（这里和word2vec一致）

经过embedding后，我们的输入维度变为(batch_size, sequence_length,embedding dimention)[batch大小，每句话的长度，嵌入维度]

②positional encodeing位置编码

由于transformer没有LSTM等RNN的循环迭代操作，所以我们必须提供每个字的位置信息给transfomer，位置嵌入实际上就是一张表，这张表的维度为(max sequence length, embedding dimention)[句子最大长，嵌入维度]，这里面句子最大长保证了我们这张表一定比输入的X矩阵要大，二者由于第二个维度相同，在实际中可以直接相加。

那么，这张表是怎么生成的呢？原文中，表是按照如下公式生成的：

这里面，pos代表了某句话中字的位置，而i则是该字中不同维度的位置，对于偶数位置使用sin，奇数位置使用cos，为什么要使用sin和cos呢？实际上，二者的周期都是2pi，在每个括号中，dmodel代表了嵌入维度，2i/dmodel的意思其实是想说明某维度在整个嵌入维度中的位置信息，2i越大，则其在某字的向量中就越靠后，对于10000来说，其开的次方也就越大，其分之1也就越小，我们将pos看作自变量，其系数在列越靠后的情况下，周期会越大，示意图如下：

这样的包含位置的纹理信息可以提供给模型顺序信息。

此外，这个矩阵如果乘以自己的转置做类似Q乘以K转置的操作，会发现，位置矩阵的主对角线元素值最大，关系最为密切，而离主对角线元素越远则关系逐渐变小。这符合我们对于词离得越进关系越大，离的越远则关系越小的假设。

那么，经过了①和②，我们的原始X变为了Embedding（X）+   Positional encoding

③multi-head attention多头注意力

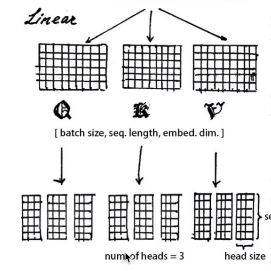
在获取了最新的矩阵之后，我们会为其分配三个权重矩阵（维度都为嵌入维度*嵌入维度）做线性变换，分别得到Q，K，V，这三个矩阵和输入矩阵的维度相同。

获取了三个不同的矩阵后，我们将每个矩阵分割为head个，注意嵌入维度必须能整除head

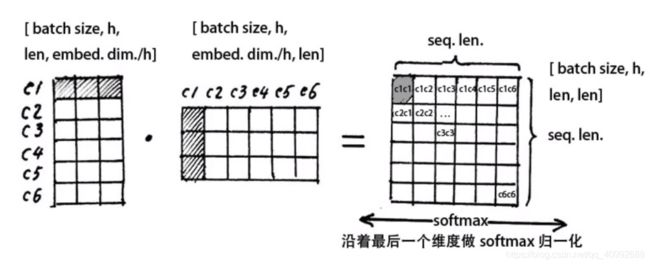
然后，对于每一个Q，都要去乘以K的转置

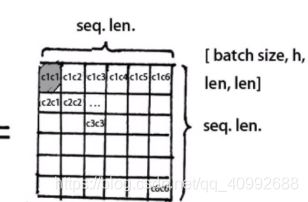
其中CiCj代表了字i与字j的关系分数，即每一行代表了当前字和其他所有字的关系。求出注意力矩阵后，我们沿着列做softmax，可以产生当前字和其他字的关系的概率权重。

需要注意的是，当Q乘以K的转置后，需要除以根号下embeding dimention，这样的话，我们可以防止QK由于维度过大导致乘积过大，而使得最后的梯度为0，相当于把注意力矩阵缩放回标准差为1的正态分布。

获取了自注意力矩阵后，我们将其乘以V，从而对每个向量进行加权求和，这样，每一个字的信息都包含了上下文的一定的信 息。

 

我们发现，Q，K，V经过运算以后最终并没有改变其维度，这也为后续能够使用残差连接埋下了伏笔。

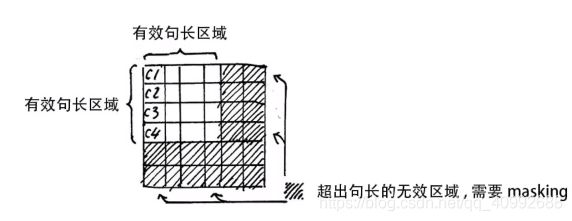
此外需要注意一点的是，由于部分句子比较短，通过补0后参与了运算，这时我们不应该用0填充，由于e的0次方为1，softmax会使得0也参与到运算之中

如图所示，c1c5，c1c6等无效，需要使用-inf代替，再通过softmax后以达到masking的目的。

④add and layer normalization 残差连接和层正则化

这里的add指的是残差连接，即将多头注意力后形成的矩阵，和原始经过embeding的矩阵求和。使用残差连接可以减缓梯度消失的问题，这里可以使得梯度跨层传到前面去。

关于layer normalization，实际上指的是对同一个字的向量进行转换，即按行求均值和标准差，然后将原始的x减去均值并除以标准差加上偏置项（防止为0）

α和β用来弥补在归一化的过程中，损失的长度信息，这两个向量的参数是可训练的。

至于为什么一定要使用层正则化而不是batchnorm呢？

这里我引用之前一位大佬的解释：

在CV任务中，我们一般使用BN，这是因为我们认为不同channel的信息比较相关，使用BN可以比较好的保留不同channel的信息，而对于NLP的任务，同一batch的不同句子相似度并不高度相关，强行在句子间进行正则化有可能会磨灭掉不同句子间的差异性。

正则化是通过把一部分不重要的复杂信息损失掉，以此来降低拟合难度以及过拟合的风险，从而加速了模型的收敛，不同的正则化方式只不过是对不同维度的信息进行损失。

⑤feedforward前馈神经网络

这一部分由两层线性映射并在第一层映射中使用激活函数激活，这里的激活函数如RELU

总结：

两次线性变换中，第一次会将维度提升，然后再将维度降低，以使得可以进行残差连接。

最终经过这一个block后，我们的X并没有因此而被改变维度。

再来看一下decoder部分：

整体上看，这里面的输入同样经过word embedding和位置向量的嵌入累加过程，然后通过mask的多头注意力模块，产生的输出在经过add和norm后作为下一层的Q，和来自encoder最后一个模块的输出K和V（K和V实际上是相同的）再次做一次多头注意力机制，然后经过add和norm，后续的操作也是经过feedforward。

那这里的Mask是为什么存在，又如何处理的呢？

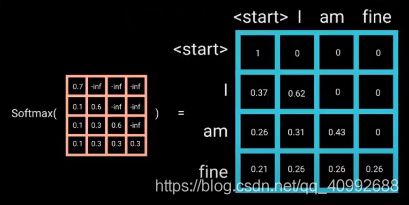
实际上，在训练阶段，由于我们要把整句话的矩阵输入decoder，但是前面的单词应该是不知道后面单词的信息的，这时，我们需要引入一个上三角为负无穷的矩阵，类似encoder部分的操作，使得其在softmax的过程中被置为0。【当然，类似于encoder部分中padding补0部分的也要被置-inf】

注意，mask在softmax操作之前进行，这可以保证我们在已知部分概率和仍然为1.