大连理工大学软件学院2022年秋季学期《矩阵与数值分析》上机作业
文章目录
- 《计算机科学计算》第二版
-
- 162页第12题(1)
- 162页第16题
- 216页第12题
- 《数值分析方法与应用》
-
- 一、基础知识部分
-
- 1、
- 5、
- 二、线性方程组求解
-
- 2、
- 6、
- 三、非线性方程组求解
-
- 1、
- 4、
- 四、插值与逼近
-
- 1、
- 5、
- 7、
- 五、数值积分
-
- 2、
- 六、微分方程数值解法
-
- 1、
《计算机科学计算》第二版
162页第12题(1)
用Newton法求 x 3 − x 2 − x − 1 = 0 x^3 - x^2 - x - 1 = 0 x3−x2−x−1=0 的根,取 x 0 = 2 x_0 = 2 x0=2,要求 x k − x k − 1 < 1 0 − 5 x_k - x_{k - 1} < 10^{-5} xk−xk−1<10−5。
解:Newton迭代法的公式为 x k + 1 = x k − f ( x k ) f ′ ( x k ) , ( k = 0 , 1 , 2 , . . . ) x_{k+1} = x_k - \frac{f(x_k)}{f'(x_k)}, (k = 0, 1, 2, ...) xk+1=xk−f′(xk)f(xk),(k=0,1,2,...),
代码如下:
from sympy import *
def g1(x):
return x ** 3 - x ** 2 - x - 1
def f(i):
x = symbols("x") # 符号x,自变量
return i - g1(i) / diff(g1(x), x).subs('x', i);
def solve(x):
y = float(f(x))
i = 1
while (not abs(y - x) < 10 ** -5):
print("第" + str(i) + "次迭代:当前解:" + str(y) + '\t' + "上一步解:" + str(x) + "\t" + "误差:" + str(abs(y - x)))
x = y
y = f(x)
i = i + 1
print("第" + str(i) + "次迭代:当前解:" + str(y) + '\t' + "上一步解:" + str(x) + "\t" + "误差:" + str(abs(y - x)))
if __name__ == '__main__':
solve(2)
运行结果如图所示:

综上:方程的解为1.83928675521416
162页第16题
Heonardo于1225年研究了方程:
f ( x ) = x 3 + 2 x 2 + 10 x − 20 = 0 , f(x) = x^3 + 2x^2 + 10x - 20 = 0, f(x)=x3+2x2+10x−20=0,
并得出一个根 α = 1.36880817 \alpha = 1.36880817 α=1.36880817,但当时无人知道他用了什么方法,这个结果在当时是个非常著名的结果,请你构造一种简单迭代来验证此结果。
解:经计算:
f ( 1.3 ) = − 1.423 , f ( 1.4 ) = 0.664 , f ( 1.3 ) ⋅ f ( 1.4 ) < 0 , 当 1.3 ≤ x ≤ 1.4 时 , f ′ ( x ) > 0 , 即 f ( x ) 在 [ 1.3 , 1.4 ] 上 有 且 仅 有 一 个 解 , 则 使 用 N e w t o n 法 进 行 求 证 : f(1.3) = -1.423, f(1.4) = 0.664, f(1.3)·f(1.4) < 0, 当1.3 \leq x \leq 1.4时, f'(x) > 0,即f(x)在[1.3, 1.4]上有且仅有一个解,则使用Newton法进行求证: f(1.3)=−1.423,f(1.4)=0.664,f(1.3)⋅f(1.4)<0,当1.3≤x≤1.4时,f′(x)>0,即f(x)在[1.3,1.4]上有且仅有一个解,则使用Newton法进行求证:
代码如下:
from sympy import *
def g1(x):
return x ** 3 + 2 * x ** 2 + 10 * x - 20
def f(i):
x = symbols("x") # 符号x,自变量
return i - g1(i) / diff(g1(x), x).subs('x', i);
def solve(x):
y = float(f(x))
i = 1
while (not abs(y - x) < 10 ** -8):
print("第" + str(i) + "次迭代:当前解:" + str(y) + '\t' + "上一步解:" + str(x) + "\t" + "误差:" + str(abs(y - x)))
x = y
y = f(x)
i = i + 1
print("第" + str(i) + "次迭代:当前解:" + str(y) + '\t' + "上一步解:" + str(x) + "\t" + "误差:" + str(abs(y - x)))
if __name__ == '__main__':
solve(1.3)
此处设置的相邻两次结果之差不大于 1 0 − 8 10^{-8} 10−8,可见最后结果为:1.36880810782137,Heonardo的结果得以验证。
216页第12题
(数值实验题)人造地球卫星的轨道可视为平面上的椭圆,地心位于椭圆的一个焦点处。已知一颗人造地球卫星近地点距地球表面439km,远地点距地球表面2384km,地球半径为6371km。求该卫星的轨道长度。
解:长半轴 a = ( 2384 + 439 + 6371 ∗ 2 ) / 2 = 7782.5 k m a = (2384 + 439 + 6371 * 2) / 2 = 7782.5km a=(2384+439+6371∗2)/2=7782.5km,半个焦距 c = a − 439 − 6371 = 972.5 k m c = a - 439 - 6371 = 972.5km c=a−439−6371=972.5km,则短半轴 b = a 2 − c 2 = 7721.5 k m b = \sqrt{a^2 - c^2} = 7721.5km b=a2−c2=7721.5km。设参数方程
{ x = 7782.5 ∗ cos t y = 7721.5 ∗ sin t \left\{ \begin{array}{l} x = 7782.5 * \cos {t}\\ y = 7721.5 * \sin {t} \end{array} \right. {x=7782.5∗costy=7721.5∗sint
其中 t ∈ [ 0 , 2 π ] t \in [0, 2\pi] t∈[0,2π]。根据弧长公式: S = ∫ α β x ′ 2 ( t ) + y ′ 2 ( t ) d t S = \int_{\alpha}^{\beta}\sqrt{x^{'2}(t) + y^{'2}(t)}dt S=∫αβx′2(t)+y′2(t)dt可知,周长积分公式如下:
L = 4 ∗ ∫ 0 π 2 ( 7782.5 ∗ sin x ) 2 + ( 7721.5 ∗ cos x ) 2 d x L = 4 * \int_{0}^{\frac{\pi}{2}} \sqrt{(7782.5*\sin{x})^2 + (7721.5*\cos{x})^2} dx L=4∗∫02π(7782.5∗sinx)2+(7721.5∗cosx)2dx
使用 G a u s s Gauss Gauss型积分公式计算上述积分,代码如下:
from sympy import *
import numpy as np
def f(x):
return sqrt(((7782.5 * sin(x)) ** 2) + ((7721.5 * cos(x)) ** 2))
def formula_cal():
a = 7782.5
b = 7721.5
res = 2 * 3.1415926 * b + 4 * (a - b)
print("公式计算轨道周长为:" + str(res) + "千米")
def cal_integrate(i):
# 权函数为1,i是需要增加的x的次数
x = symbols('x')
res = integrate(x ** i, (x, 0, 3.1415926 / 2))
return res
def gauss_points(n):
# 点的个数减一
A = Matrix(np.zeros((n + 2, n + 2)))
for i in range(0, n + 2):
for j in range(0, n + 1):
A[i, j] = cal_integrate(i + j)
x = symbols('x')
for i in range(0, n + 2):
A[i, n + 1] = x ** i
result = solve(det(A), x)
return result
def gauss_cosfficient(n):
# 点的个数减一
b = gauss_points(n)# 拿到n个求积节点
A = []
x1 = []
for i in range(0, len(b)):
x1.append(f(b[i]))
x = symbols('x')
expr = 1.0 # 权函数
for j in range(0, len(b)):
if(j != i):
expr = expr * ((x - b[j]) ** 2) / ((b[i] - b[j]) ** 2)
A.append(integrate(expr, (x, 0, 3.1415926 / 2)))
gauss_solve(x1, A)
def gauss_solve(x1, A):
n = len(x1)
result = 0.0
for i in range(0, n):
result = result + x1[i] * A[i]
print(str(n) + "点Gauss型积分求轨道周长为:" + str(result * 4) + "千米")
if __name__ == '__main__':
gauss_cosfficient(1)
gauss_cosfficient(4)
formula_cal()
其中计算轨道周长的公式为 L = 2 π b + 4 ( a − b ) L = 2 \pi b + 4(a-b) L=2πb+4(a−b),通过结果可以看出使用 G a u s s Gauss Gauss型积分求解与使用公式求解的结果大致相等,正确性得到了验证。
《数值分析方法与应用》
一、基础知识部分
1、
设 S N = ∑ j = 2 N 1 j 2 − 1 S_N = \sum_{j = 2}^{N} \frac{1}{j^2 - 1} SN=∑j=2Nj2−11,其精确值为 1 2 ( 3 2 − 1 N − 1 N + 1 ) \frac{1}{2}(\frac{3}{2} - \frac{1}{N} - \frac{1}{N + 1}) 21(23−N1−N+11)。
(1)编制按从大到小的顺序 S N = 1 2 2 − 1 + 1 3 2 − 1 + ⋅ ⋅ ⋅ + 1 N 2 − 1 S_N = \frac{1}{2^2 - 1} + \frac{1}{3^2 - 1} + ··· + \frac{1}{N^2 - 1} SN=22−11+32−11+⋅⋅⋅+N2−11,计算 S N S_N SN的通用程序。
(2)编制按从小到大的顺序 S N = 1 N 2 − 1 + 1 ( N − 1 ) 2 − 1 + ⋅ ⋅ ⋅ + 1 2 2 − 1 S_N = \frac{1}{N^2 - 1} + \frac{1}{(N - 1)^2 - 1} + ··· + \frac{1}{2^2 - 1} SN=N2−11+(N−1)2−11+⋅⋅⋅+22−11,计算 S N S_N SN的通用程序。
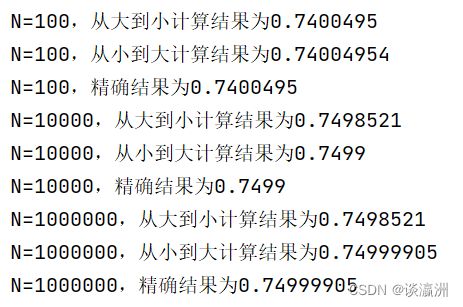
(3)按两种顺序分别计算 S 1 0 2 S_{10^2} S102, S 1 0 4 S_{10^4} S104, S 1 0 6 S_{10^6} S106,并指出有效位数(编制程序时用单精度)。
(4)通过本上机题,你明白了什么。
解:代码如下:
import numpy as np
def f1(n):
#从大到小
res = np.float32(0.0)
for i in range(2, n + 1):
res = res + np.float32(1) / np.float32(i ** 2 - 1)
print("N=" + str(n) + ",从大到小计算结果为" + str(np.float32(res)))
def f2(n):
#从小到大
res = np.float32(0)
for i in reversed(range(2, n + 1)):
res = res + np.float32(1) / np.float32(i ** 2 - 1)
print("N=" + str(n) + ",从小到大计算结果为" + str(np.float32(res)))
def f3(n):
#精确结果
res = np.float32(3 * n * n - n - 2) / np.float32(4 * n * n + 4 * n)
print("N=" + str(n) + ",精确结果为" + str(np.float32(res)))
if __name__ == '__main__':
f1(100)
f2(100)
f3(100)
f1(10000)
f2(10000)
f3(10000)
f1(1000000)
f2(1000000)
f3(1000000)
由于 p y t h o n python python默认的都是双精度的浮点数,所以在这里我们用numpy.float32()来进行强制转换,将数据变成单精度的浮点数。
运行结果如图所示:
有效位数如下表所示:
| 从大到小 | 从小到大 | |
|---|---|---|
| 1 0 2 10^2 102 | 7位 | 7位 |
| 1 0 4 10^4 104 | 4位 | 4位 |
| 1 0 6 10^6 106 | 3位 | 8位 |
通过上述实验数据可以看出:
(1)计算机存在舍入误差,有时会导致计算结果与精确结果略有出入;
(2)随着N的增大,有些分母会变得非常大,此时舍入误差的现象会变得很明显;
(3)此次算法使用从小到大的顺序进行得到的数据相对而言更精确,可以得到这样的启示:在数值计算时,要先分析不同算法对结果的影响,避免**“大数吃小数”**的现象,找出能得到更精确的结果的算法。
5、
首先编制一个利用秦九韶算法计算一个多项式在给定点的函数值的通用程序,程序包括输入多项式的系数以及给定点,输出函数值,利用编制的程序计算
p ( x ) = ( x − 2 ) 9 = x 9 − 18 x 8 + 144 x 7 − 672 x 6 + 2016 x 5 − 4032 x 4 + 5376 x 3 − 4608 x 2 + 2304 x − 512 p(x) = (x - 2)^9 = x^9 - 18x^8 + 144x^7 - 672x^6 + 2016x^5 - 4032x^4 + 5376x^3 -4608x^2 + 2304x - 512 p(x)=(x−2)9=x9−18x8+144x7−672x6+2016x5−4032x4+5376x3−4608x2+2304x−512
在 x = 2 x = 2 x=2邻域附近的值,画出 p ( x ) p(x) p(x)在 x ∈ [ 1.95 , 2.05 ] x \in [1.95, 2.05] x∈[1.95,2.05]上的图像。
解:代码如下:
import numpy as np
import matplotlib.pyplot as plt
def QJS(a, x):
'''
:param a: 系数向量
:param x: 给定点
:return: 无
'''
res = 0.0
if len(a) == 0:
print("没有参数")
else:
res = a[0]
for i in range(1, len(a)):
res = res * x + a[i]
print("函数在x = " + str(x) + "时的值为:" + str(res))
def graph_function(a):
'''
:param a: 系数向量
:return: 无
'''
x = np.arange(1.95, 2.05, 0.01)
y = a[0] * x ** 9 + a[1] * x ** 8 + a[2] * x ** 7 + a[3] * x ** 6 + a[4] * x ** 5 + a[5] * x ** 4 + a[6] * x ** 3 + a[7] * x ** 2 + a[8] * x + a[9]
plt.figure()
plt.plot(x, y, linestyle = '-', color = 'red')
plt.xlabel('x')
plt.ylabel('y')
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
plt.show()
if __name__ == '__main__':
a = [1, -18, 144, -672, 2016, -4032, 5376, -4608, 2304, -512]# 多项式系数向量
x_0 = 2.03# 给定点
QJS(a, x_0)# 计算x = 2邻域附近的值
graph_function(a)# p(x)在[1.95, 2.05]上的图像
计算 x = 2 x = 2 x=2邻域附近的值(此处取2.03):
![]()
画出 p ( x ) p(x) p(x)在 x ∈ [ 1.95 , 2.05 ] x \in [1.95, 2.05] x∈[1.95,2.05]上的图像:
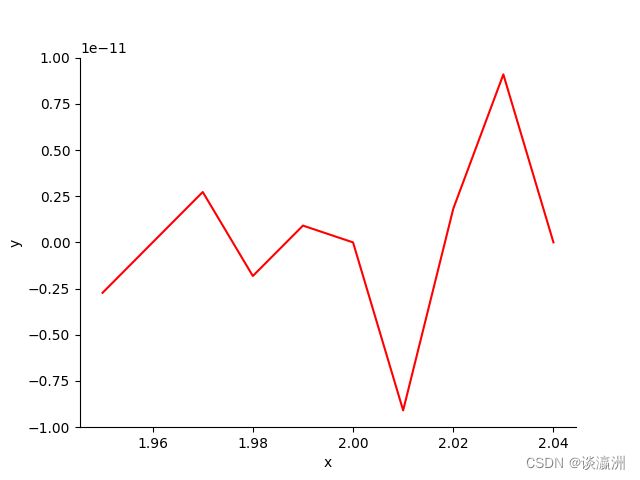
二、线性方程组求解
2、
编制程序求解矩阵A的Cholesky分解,并用程序求解方程组 A x = b Ax = b Ax=b,其中
A = [ 7 1 − 5 1 1 9 2 7 − 5 2 7 − 1 1 7 − 1 9 ] , b = ( 13 , − 9 , 6 , 0 ) T A = \left[\begin{array}{r} 7 & 1 & -5 & 1\\ 1 & 9 & 2 & 7\\ -5 & 2 & 7 & -1\\ 1 & 7 & -1 & 9\\ \end{array}\right], b = (13, -9, 6, 0)^T A=⎣⎢⎢⎡71−511927−527−117−19⎦⎥⎥⎤,b=(13,−9,6,0)T
解:代码如下:
import numpy as np
from scipy import linalg
def cholesky_resolve(A):
# Cholesky分解,返回L矩阵和L转置
L = linalg.cholesky(A, lower = True)
L_T = linalg.cholesky(A)
return [L, L_T]
def solve_lower(A, b):
# 计算Ax = b,其中A是下三角矩阵,返回x
n = np.shape(A)[0]
x = np.zeros((n, 1))
for i in range(0, n):
res = 0.0
for j in range(0, i):
res = res + x[j] * A[i][j]
x[i] = (b[i] - res) / A[i][i]
return x
def solve_upper(A, b):
# 计算Ax = b,其中A是上三角矩阵,返回x
n = np.shape(A)[0]
x = np.zeros((n, 1))
for i in reversed(range(0, n)):
res = 0.0
for j in range(i + 1, n):
res = res + x[j] * A[i][j]
x[i] = (b[i] - res) / A[i][i]
return x
if __name__ == '__main__':
A = np.array([[7, 1, -5, 1],[1, 9, 2, 7],[-5, 2, 7, -1],[1, 7, -1, 9]])
b = np.array([13, -9, 6, 0])
res = cholesky_resolve(A)
L = res[0]
L_T = res[1]
y = solve_lower(L, b)
x = solve_upper(L_T, y)
print("x = \n", x)
运行结果如图所示:

本题运用Cholesky分解将对称正定矩阵A分解为 A = L L T A = LL^T A=LLT,其中L是对角元均为正数的下三角矩阵,然后利用公式:
{ L y = b L T x = y \left\{ \begin{array}{l} Ly = b\\ L^Tx = y \end{array} \right. {Ly=bLTx=y
进行求解。
6、
令 H H H表示 n × n n \times n n×n的Hilbert矩阵,其中 ( i , j ) (i, j) (i,j)元素是 1 / ( i + j − 1 ) 1/(i + j - 1) 1/(i+j−1), b b b是元素全为1的向量,用Gauss消去法求解 H x = b Hx = b Hx=b,其中取 ( 1 ) n = 2 ; ( 2 ) n = 5 ; ( 3 ) n = 10 (1) n = 2;(2) n = 5;(3) n = 10 (1)n=2;(2)n=5;(3)n=10。
解:代码如下:
import numpy as np
def create_augment(n):
# 创建系数矩阵为Hilbert矩阵,b均为1的增广矩阵
H = np.zeros((n, n + 1))
for i in range(n):
for j in range(n):
H[i][j] = 1.0 / (i + j + 1)
H[i][n] = 1.0
return H
def solve_upper(A, b):
# 计算Ax = b,其中A是上三角矩阵,返回x
n = np.shape(A)[0]
x = np.zeros((n, 1))
for i in reversed(range(0, n)):
res = 0.0
for j in range(i + 1, n):
res = res + x[j] * A[i][j]
x[i] = (b[i] - res) / A[i][i]
return x
def gauss_solve(n):
# 使用Gauss消元法将增广矩阵化成行阶梯型,并求解,返回x
A = create_augment(n)
for i in range(0, n - 1):
for j in range(i + 1, n):
alpha = A[j][i]/A[i][i]
for k in range(i, n + 1):
A[j][k] = A[j][k] - alpha * A[i][k]
tempA = np.zeros((n, n))
b = np.zeros((n, 1))
for i in range(0, n):
for j in range (0, n):
tempA[i][j] = A[i][j]
for i in range(0, n):
b[i] = A[i][n]
return solve_upper(tempA, b)
if __name__ == '__main__':
x_2 = gauss_solve(2)
x_5 = gauss_solve(5)
x_10 = gauss_solve(10)
print("x_2 = \n", x_2)
print("x_5 = \n", x_5)
print("x_10 = \n", x_10)
运行结果如图所示:
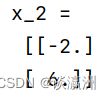

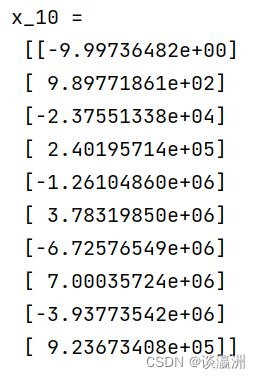
x _ 2 , x _ 5 , x _ 10 x\_2, x\_5, x\_10 x_2,x_5,x_10分别是以2阶、5阶、10阶 H i l b e r t Hilbert Hilbert矩阵为系数矩阵, b b b全为1的线性方程组的解。
三、非线性方程组求解
1、
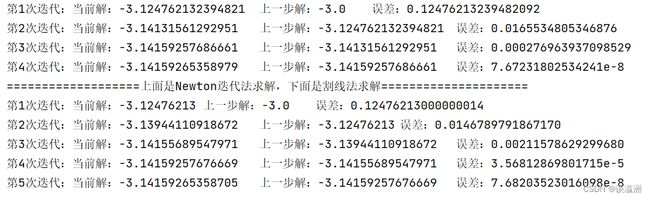
分别应用Newton迭代法和割线法计算(1)非线性方程 2 x 3 − 5 x + 1 = 0 2x^3 - 5x + 1 = 0 2x3−5x+1=0在 [ 1 , 2 ] [1,2] [1,2]上的一个根;(2) e x sin x = 0 e^x\sin x = 0 exsinx=0在 [ − 4 , − 3 ] [-4, -3] [−4,−3]上的一个根。
使用割线法时,由于迭代计算新的值需要前两个值,所以除了初始值之外,我们需要手动计算一个值;也可以先采用 N e w t o n Newton Newton迭代法先计算出来第二个值,然后代入到割线法中。
(1)使用 N e w t o n Newton Newton迭代法和割线法计算非线性方程 2 x 3 − 5 x + 1 = 0 2x^3 - 5x + 1 = 0 2x3−5x+1=0在 [ 1 , 2 ] [1,2] [1,2]上的一个根:
解:代码如下:
from sympy import *
def g1(x):
return 2.0 * x ** 3 - 5.0 * x + 1.0
def newton(i):
x = symbols("x") # 符号x,自变量
return i - g1(i) / diff(g1(x), x).subs('x', i)
def secant(x_1, x_2):
return x_2 - (g1(x_2) / (g1(x_2) - g1(x_1))) * (x_2 - x_1)
def newton_solve(x):
y = float(newton(x))
i = 1
while (not abs(y - x) < 10 ** -5):
print("第" + str(i) + "次迭代:当前解:" + str(y) + '\t' + "上一步解:" + str(x) + "\t" + "误差:" + str(abs(y - x)))
x = y
y = newton(x)
i = i + 1
print("第" + str(i) + "次迭代:当前解:" + str(y) + '\t' + "上一步解:" + str(x) + "\t" + "误差:" + str(abs(y - x)))
def secant_solve(x_1, x_2):
a = x_1
b = x_2
i = 1# 第一步笔算,先走一步得到两个值
while(not abs(b - a) < 10 ** -5):
print("第" + str(i) + "次迭代:当前解:" + str(b) + '\t' + "上一步解:" + str(a) + "\t" + "误差:" + str(abs(b - a)))
c = secant(a, b)
a = b
b = c
i = i + 1
print("第" + str(i) + "次迭代:当前解:" + str(b) + '\t' + "上一步解:" + str(a) + "\t" + "误差:" + str(abs(b - a)))
if __name__ == '__main__':
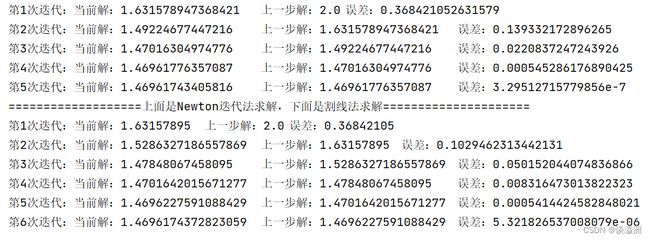
newton_solve(2.0)# 初始值选择2.0
print("===================上面是Newton迭代法求解,下面是割线法求解=====================")
secant_solve(2.0, 1.63157895)# 初始值选择2.0,第二个值是第一步采用切线法算出来的
运行结果如图所示:
(2)使用 N e w t o n Newton Newton迭代法和割线法计算非线性方程 e x sin x = 0 e^x\sin x = 0 exsinx=0在 [ − 4 , − 3 ] [-4, -3] [−4,−3]上的一个根;
解:代码如下:
from sympy import *
def g1(x):
return E ** x * sin(x)
def newton(i):
x = symbols("x") # 符号x,自变量
return i - g1(i) / diff(g1(x), x).subs('x', i)
def secant(x_1, x_2):
return x_2 - (g1(x_2) / (g1(x_2) - g1(x_1))) * (x_2 - x_1)
def newton_solve(x):
y = float(newton(x))
i = 1
while (not abs(y - x) < 10 ** -5):
print("第" + str(i) + "次迭代:当前解:" + str(y) + '\t' + "上一步解:" + str(x) + "\t" + "误差:" + str(abs(y - x)))
x = y
y = newton(x)
i = i + 1
print("第" + str(i) + "次迭代:当前解:" + str(y) + '\t' + "上一步解:" + str(x) + "\t" + "误差:" + str(abs(y - x)))
def secant_solve(x_1, x_2):
a = x_1
b = x_2
i = 1# 第一步笔算,先走一步得到两个值
while(not abs(b - a) < 10 ** -5):
print("第" + str(i) + "次迭代:当前解:" + str(b) + '\t' + "上一步解:" + str(a) + "\t" + "误差:" + str(abs(b - a)))
c = secant(a, b)
a = b
b = c
i = i + 1
print("第" + str(i) + "次迭代:当前解:" + str(b) + '\t' + "上一步解:" + str(a) + "\t" + "误差:" + str(abs(b - a)))
if __name__ == '__main__':
newton_solve(-3.0)# 初始值选择-3.0
print("===================上面是Newton迭代法求解,下面是割线法求解=====================")
secant_solve(-3.0, -3.12476213)# 初始值选择-3.0,第二个值是第一步采用切线法算出来的
4、
用 N e w t o n Newton Newton迭代法求解方程 x 3 + x 2 + x − 3 = 0 x^3 + x^2 + x - 3 = 0 x3+x2+x−3=0的根,初值选择 x 0 = − 0.7 x_0 = -0.7 x0=−0.7,迭代7步并与真值 x ∗ = 1 x^* = 1 x∗=1相比较,并列出数据表(表1)。
数据表(表 1)
| i i i | x i x_i xi | e i = ∣ x i − x ∗ ∣ e_i = \vert x_i - x^* \vert ei=∣xi−x∗∣ | e i e i − 1 2 \frac{e_i}{e_{i - 1}^2} ei−12ei |
|---|---|---|---|
| 0 | -0.7 | 0.3 | 无 |
| 1 | 2.6205607476635517 | 1.6205607476635517 | 0.560747663551402 |
| 2 | 1.70844019026256 | 0.708440190262561 | 0.269756898741237 |
| 3 | 1.20637869801811 | 0.206378698018109 | 0.411205094190995 |
| 4 | 1.02416166412510 | 0.0241616641251030 | 0.567279521785564 |
| 5 | 1.00038149112102 | 0.000381491121020261 | 0.653477665330685 |
| 6 | 1.00000009699281 | 9.69928142247056e-8 | 0.666454786687556 |
| 7 | 1.00000000000001 | 6.21724893790088e-15 | 0.660874714617131 |
解:代码如下:
from sympy import *
def g1(x):
return x ** 3 + x ** 2 + x - 3.0
def newton(i):
x = symbols("x") # 符号x,自变量
return i - g1(i) / diff(g1(x), x).subs('x', i)
def newton_solve(x):
y = float(newton(x))
i = 1
while (i < 7):
print("第" + str(i) + "次迭代:当前解:" + str(y) + '\t' + "误差:" + str(abs(y - 1.0)) + "\t" + "平方收敛系数" + str(abs(y - 1.0) / (abs(x - 1.0) * abs(x - 1.0))))
x = y
y = newton(x)
i = i + 1
print("第" + str(i) + "次迭代:当前解:" + str(y) + '\t' + "误差:" + str(abs(y - 1.0)) + "\t" + "平方收敛系数" + str(abs(y - 1.0) / (abs(x - 1.0) * abs(x - 1.0))))
if __name__ == '__main__':
newton_solve(-0.7)
四、插值与逼近
1、
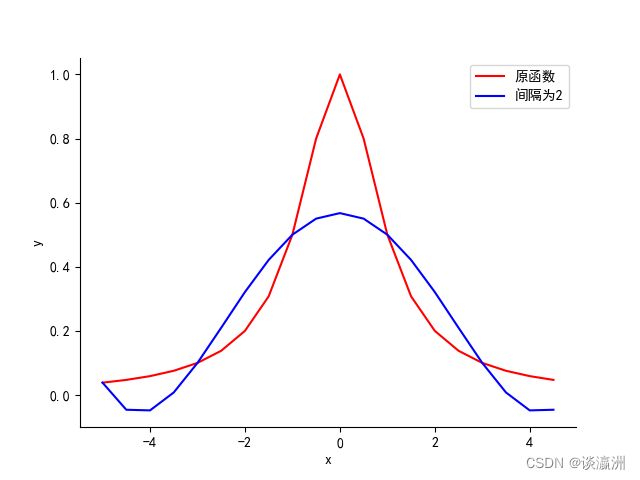
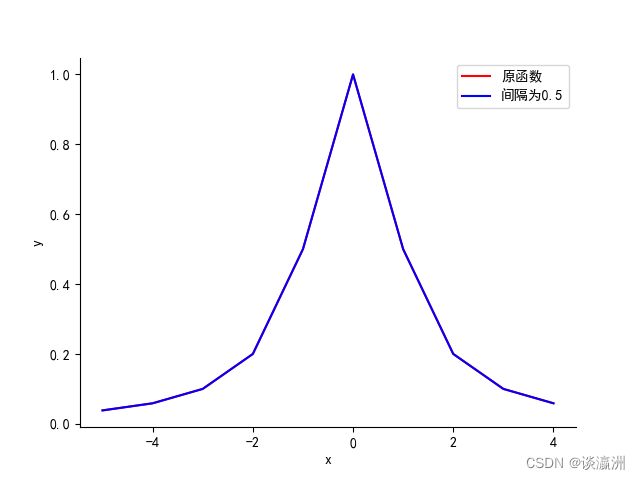
已知函数 f ( x ) = 1 1 + x 2 f(x) = \frac{1}{1 + x^2} f(x)=1+x21,在 [ − 5 , 5 ] [-5, 5] [−5,5]上分别取 2 , 1 , 1 2 2, 1, \frac{1}{2} 2,1,21为单位长度的等距节点作为插值节点,用Lagrange方法插值,并把原函数图与插值函数图比较,观察插值效果。
解:代码如下:
from sympy import *
import numpy as np
import matplotlib.pyplot as plt
from pylab import *
def g1(x):
return 1.0 / (x * x + 1.0)
def create_table(x):
# 以x为单位长度划分区间
A = np.zeros((int(10 / x + 1), 2))
i = 0
flag = -5.0
while (flag <= 5):
A[i][0] = flag
A[i][1] = g1(flag)
i = i + 1
flag = flag + x
return A
def lagrange(x):
# 求插值多项式
A = create_table(x)
m = shape(A)[0]
x = symbols('x')
y = 0.0 * x
for i in range(0, m):
temp = x ** 0.0
for j in range(0, m):
if(j == i):
continue
temp = temp * (x - A[j][0]) / (A[i][0] - A[j][0])
y = y + A[i][1] * temp
y = expand(y)
return y
def draw_graph():
'''
由于四个函数图像放在一张图里面绘制出来的图像很不直观,所以笔者选择绘制三张图象,每幅图像里面都包含一个原函数和一个求出来的Lagrange插值多项式
其中红色图像是原函数,蓝色图像是Lagrange插值多项式
'''
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体(解决中文无法显示的问题)
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像时负号“-”显示方块的问题
x = np.arange(-5.0, 5.0, 0.5)
y_0 = 1.0 / (x * x + 1)
y_1 = 0.00192307692307692 * x ** 4 - 0.0692307692307692 * x ** 2 - 5.55111512312578e-17 * x + 0.567307692307692
y_2 = -2.26244343891403e-5 * x ** 10 - 1.70465380634928e-20 * x ** 9 + 0.00126696832579186 * x ** 8 - 9.14795583034644e-20 * x ** 7 - 0.0244117647058824 * x ** 6 + 1.90819582357449e-17 * x ** 5 + 0.19737556561086 * x ** 4 + 6.96057794735694e-17 * x ** 3 - 0.67420814479638 * x ** 2 - 1.52764086103208e-16 * x + 1.0
y_3 = 2.72817068149799e-9 * x ** 20 - 4.54173855079897e-23 * x ** 19 - 2.65314598775676e-7 * x ** 18 - 6.38649607339942e-20 * x ** 17 + 1.07425130797328e-5 * x ** 16 + 5.45325105398239e-18 * x ** 15 - 0.000236412102809865 * x ** 14 - 1.08589623838001e-16 * x ** 13 + 0.00310184793200539 * x ** 12 - 4.45315713557687e-15 * x ** 11 - 0.0251135266738683 * x ** 10 - 1.78681939036474e-15 * x ** 9 + 0.126252909857137 * x ** 8 - 2.24466712578364e-14 * x ** 7 - 0.391630076762948 * x ** 6 + 4.11996825544492e-18 * x ** 5 + 0.753353962815142 * x ** 4 - 8.79743326798188e-15 * x ** 3 - 0.965739184991246 * x ** 2 - 7.99057001121817e-17 * x + 1.0
plt.figure()
plt.plot(x, y_0, linestyle='-', color='red', label='原函数')
plt.plot(x, y_1, linestyle = '-', color = 'blue', label = '间隔为2')
#plt.plot(x, y_2, linestyle = '-', color = 'blue', label = '间隔为1')
#plt.plot(x, y_3, linestyle = '-', color = 'blue', label = '间隔为0.5')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc=0)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
plt.show()
if __name__ == '__main__':
y_1 = lagrange(2)
y_2 = lagrange(1)
y_3 = lagrange(0.5)
print("y_1 = ", y_1)
print("y_2 = ", y_2)
print("y_3 = ", y_3)
draw_graph()
运行结果如图所示:
![]()
由于受到宽度限制,截图并没有显示出全部结果,下方采用文本复制的方式给出最终结果:
y_1 = 0.00192307692307692 * x ** 4 - 0.0692307692307692 * x ** 2 - 5.55111512312578e-17 * x + 0.567307692307692
y_2 = -2.26244343891403e-5 * x ** 10 - 1.70465380634928e-20 * x ** 9 + 0.00126696832579186 * x ** 8 - 9.14795583034644e-20 * x ** 7 - 0.0244117647058824 * x ** 6 + 1.90819582357449e-17 * x ** 5 + 0.19737556561086 * x ** 4 + 6.96057794735694e-17 * x ** 3 - 0.67420814479638 * x ** 2 - 1.52764086103208e-16 * x + 1.0
y_3 = 2.72817068149799e-9 * x ** 20 - 4.54173855079897e-23 * x ** 19 - 2.65314598775676e-7 * x ** 18 - 6.38649607339942e-20 * x ** 17 + 1.07425130797328e-5 * x ** 16 + 5.45325105398239e-18 * x ** 15 - 0.000236412102809865 * x ** 14 - 1.08589623838001e-16 * x ** 13 + 0.00310184793200539 * x ** 12 - 4.45315713557687e-15 * x ** 11 - 0.0251135266738683 * x ** 10 - 1.78681939036474e-15 * x ** 9 + 0.126252909857137 * x ** 8 - 2.24466712578364e-14 * x ** 7 - 0.391630076762948 * x ** 6 + 4.11996825544492e-18 * x ** 5 + 0.753353962815142 * x ** 4 - 8.79743326798188e-15 * x ** 3 - 0.965739184991246 * x ** 2 - 7.99057001121817e-17 * x + 1.0
通过对比上面三幅函数图像可知,插值得到的多项式在已知点的函数值与原函数对应的函数值是严格相等的,则这就意味着,在一定范围内,这样的函数点越多,得到的图像就与原函数越逼近。
5、
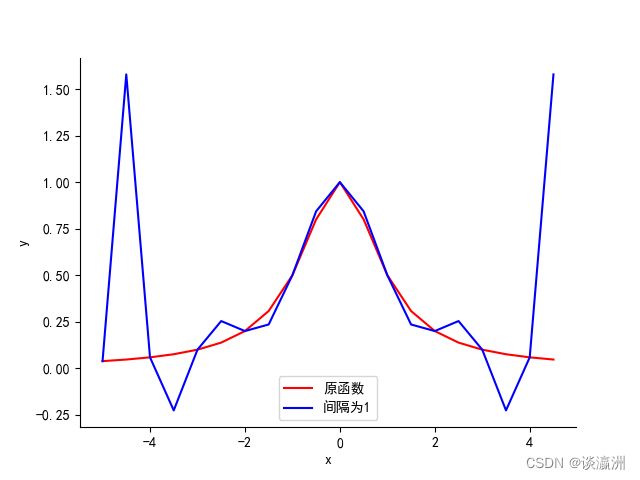
考虑函数 f ( x ) = sin π x , x ∈ [ 0 , 1 ] f(x) = \sin \pi x, x \in [0, 1] f(x)=sinπx,x∈[0,1]。用等距节点作 f ( x ) f(x) f(x)的 N e w t o n Newton Newton插值,画出插值多项式以及 f ( x ) f(x) f(x)的图像,观察收敛性。
解:代码如下:
from sympy import *
import numpy as np
import matplotlib.pyplot as plt
from pylab import *
def g1(x):
return sin(pi * x)
def create_table(x):
# 以x为单位长度划分区间
A = np.zeros((int(1.0 / x + 1), int(1.0 / x + 1) + 1))
i = 0
flag = 0.0
while (flag <= 1.0):
A[i][0] = flag
A[i][1] = g1(flag)
i = i + 1
flag = flag + x
return A
def lagrange(x):
# 求插值多项式
A = create_table(x)
m = shape(A)[0]
n = shape(A)[1]
# 求矩阵
for i in range(2, n):
for j in range(i - 1, m):
A[j][i] = (A[j][i-1] - A[j-1][i-1]) / (A[j][0] - A[j-i+1][0])
# 生成Newton多项式
x = symbols('x')
y = A[0][1] * x ** 0
for i in range(1, m):
temp = x ** 0.0
for j in range(0, i):
temp = temp * (x - A[j][0])
y = y + A[i][i+1] * temp
y = expand(y)
return y
def draw_graph():
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体(解决中文无法显示的问题)
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像时负号“-”显示方块的问题
x = np.arange(-0.1, 1.1, 0.1)
y_0 = sin(pi * x)
y_1 = 3.61347072168978 * x ** 4 - 7.22694144337956 * x ** 3 + 0.517968210332188 * x ** 2 + 3.09550251135759 * x
plt.figure()
plt.plot(x, y_0, linestyle='-', color='red', label='原函数')
plt.plot(x, y_1, linestyle = '-', color = 'blue', label = 'Newton插值多项式')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc=0)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
plt.show()
if __name__ == '__main__':
y = lagrange(0.2)# 节点间距为0.2
print("y = ", y)
draw_graph()
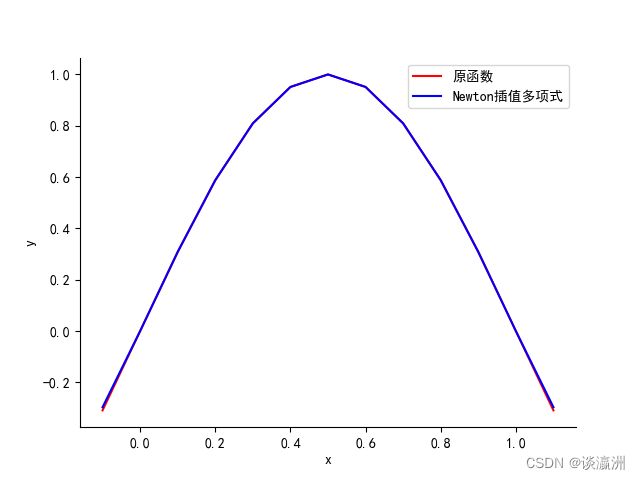
运行结果如图所示:
![]()
上方的函数即为 N e w t o n Newton Newton插值生成的多项式函数,当前节点间距为0.2,生成函数与原函数图像对比(红色曲线为原函数,蓝色曲线为Newton多项式)如图所示:
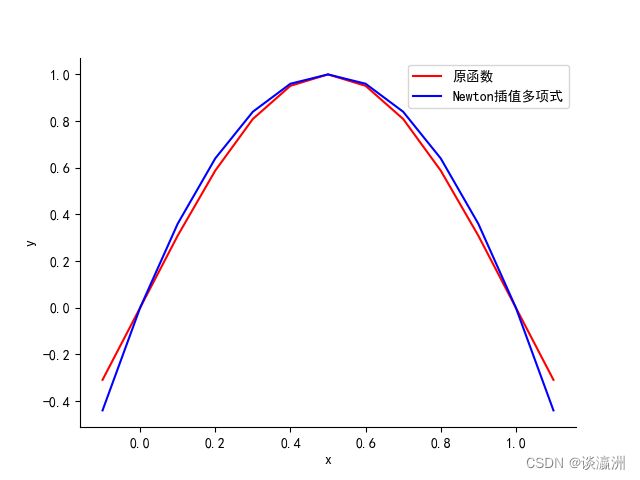
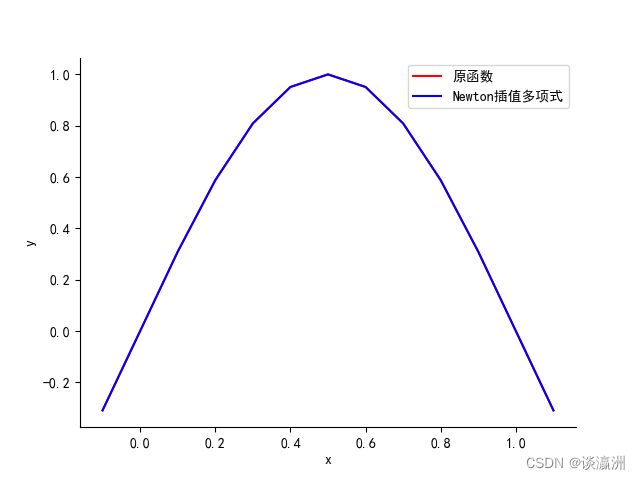
可见在[0,1]这个区间上,生成多项式的收敛性还是比较好的。下面附上几个不同间距的生成多项式与原函数对比:
Newton插值多项式:y = -4.0*x**2 + 4.0*x
Newton插值多项式:y = -0.024766311852928*x**10 + 0.123831559266328*x**9 - 0.0434827562171139*x**8 - 0.569058330736058*x**7 - 0.0143385072780853*x**6 + 2.55481222833824*x**5 - 0.00100448543439632*x**4 - 5.16757591409148*x**3 - 1.04708062454788e-5*x**2 + 3.14159298881174*x
可见节点间距为0.5时收敛性一般,间距为0.2时收敛性有所好转,间距为0.1时收敛性比前两者都要好。
7、
编程计算三次样条 S S S,满足 S ( 0 ) = 1 , S ( 1 ) = 3 , S ( 2 ) = 3 , S ( 3 ) = 4 , S ( 4 ) = 2 S(0) = 1, S(1) = 3, S(2) = 3, S(3) = 4, S(4) = 2 S(0)=1,S(1)=3,S(2)=3,S(3)=4,S(4)=2,其中边界条件 S ′ ′ ( 0 ) = S ′ ′ ( 4 ) = 0 S''(0) = S''(4) = 0 S′′(0)=S′′(4)=0。
解:使用第二类边界条件,代码如下:
import numpy as np
from sympy import *
def generate_g0(xy):
return (3.0 * (xy[1][1] - xy[1][0]) / (xy[0][1] - xy[0][0])) - ((xy[0][1] - xy[0][0]) / 2.0 * 0)
def generate_g4(xy):
return (3.0 * (xy[1][4] - xy[1][3]) / (xy[0][4] - xy[0][3])) - ((xy[0][4] - xy[0][3]) / 2.0 * 0)
def spline_solve(xy):
# 生成系数矩阵
A = np.zeros((5,5))
A[0][0] = 2.0
A[4][4] = 2.0
A[0][1] = 1.0
A[4][3] = 1.0
for i in range(1, 4):
A[i][i - 1] = 0.5
A[i][i] = 2
A[i][i + 1] = 0.5
# 生成列向量g
g = np.zeros((5, 1))
g[0][0] = generate_g0(xy)
g[4][0] = generate_g4(xy)
for i in range(1, 4):
g[i][0] = 3.0 / 2.0 * (((xy[1][i + 1] - xy[1][i]) / (xy[0][i + 1] - xy[0][i])) + ((xy[1][i] - xy[1][i - 1]) / (xy[0][i] - xy[0][i - 1])))
# 求解Am = g
m = np.linalg.solve(A, g)
# 生成多项式
for i in range(0, 4):
x = symbols('x')
s = (1 + 2 * (x - xy[0][i])) * ((x - xy[0][i + 1]) ** 2) * xy[1][i] + (1 - 2 * (x - xy[0][i + 1])) * ((x - xy[0][i]) ** 2) * xy[1][i + 1] + (x - xy[0][i]) * ((x - xy[0][i + 1]) ** 2) * m[i][0] + (x - xy[0][i + 1]) * ((x - xy[0][i]) ** 2) * m[i + 1][0]
s = expand(s)
print("x属于[" + str(i) + ", " + str(i+1) + "]时,s(x) = ", s)
if __name__ == '__main__':
xy = np.array([[0.0, 1.0, 2.0, 3.0, 4.0], [1.0, 3.0, 3.0, 4.0, 2.0]])
spline_solve(xy)
运行结果如图所示:

经验证,第二段函数和第一段函数之间的差大约等于 1.9643 ∗ ( x − 1 ) 3 1.9643*(x - 1)^3 1.9643∗(x−1)3,第三段函数和第二段函数之间的差大约等于 − 2.8572 ∗ ( x − 2 ) 3 -2.8572*(x - 2)^3 −2.8572∗(x−2)3,第四段函数和第三段函数之间的差大约等于 2.4643 ∗ ( x − 3 ) 3 2.4643*(x - 3)^3 2.4643∗(x−3)3,所以该分片函数是所求的三次样条函数。
五、数值积分
2、
用两点,三点和五点的Gauss型积分公式分别计算定积分,并与真值作比较。
S = ∫ 0 π 2 x 2 cos x d x S = \int_{0}^{\frac{\pi}{2}} x^2\cos x dx S=∫02πx2cosxdx
解:为了便于观察结果,程序中所有的 π \pi π均使用近似值 3.1415926 3.1415926 3.1415926代替,否则结果中均带有 π \pi π,不利于比较。
代码如下:
from sympy import *
import numpy as np
def f(x):
return cos(x)
def real_integrate():
# 真值
x = symbols('x')
res = integrate((x ** 2) * cos(x), (x, 0, 3.1415926 / 2))
print("真值为:" + str(res))
def cal_integrate(i):
# 权函数为x平方,i是还需要增加的次数
x = symbols('x')
res = integrate(x ** (2 + i), (x, 0, 3.1415926 / 2))
return res
def gauss_points(n):
# 点的个数减一
A = Matrix(np.zeros((n + 2, n + 2)))
for i in range(0, n + 2):
for j in range(0, n + 1):
A[i, j] = cal_integrate(i + j)
x = symbols('x')
for i in range(0, n + 2):
A[i, n + 1] = x ** i
result = solve(det(A), x)
return result
def gauss_cosfficient(n):
# 点的个数减一
b = gauss_points(n)# 拿到n个求积节点
A = []
x1 = []
for i in range(0, len(b)):
x1.append(f(b[i]))
x = symbols('x')
expr = x ** 2
for j in range(0, len(b)):
if(j != i):
expr = expr * ((x - b[j]) ** 2) / ((b[i] - b[j]) ** 2)
A.append(integrate(expr, (x, 0, 3.1415926 / 2)))
gauss_solve(x1, A)
def gauss_solve(x1, A):
n = len(x1)
result = 0.0
for i in range(0, n):
result = result + x1[i] * A[i]
print(str(n) + "点Gauss型积分为:" + str(result))
if __name__ == '__main__':
gauss_cosfficient(1)
gauss_cosfficient(2)
gauss_cosfficient(4)
real_integrate()
运行结果如图所示:

其中3点 G a u s s Gauss Gauss型积分得到的结果带有虚数,比较长,在下方另行给出:
3点Gauss型积分为:(0.518479879429716 - 1.13170196486494e-23*I)*(0.566819007009947 + 8.17802788116717e-24*I) + (0.116082467091191 + 5.82713089875272e-24*I)*(0.894546194955815 - 2.95783579853275e-24*I) + (0.114407705350449 + 1.31479879463766e-23*I)*(0.609026654797592 + 6.18118654397656e-23*I)
在此算法中,笔者采用的是按照 H e r m i t e Hermite Hermite基函数得到的求积系数公式。从结果可以看出,有着最高代数精度的 G a u s s Gauss Gauss型求积公式,在有两点的时候就已经很接近真实结果了。
六、微分方程数值解法
1、
已知常微分方程
{ d u d x = 2 x u + x 2 e x x ∈ [ 1 , 2 ] , u ( 1 ) = 0 \left\{ \begin{array}{l} \frac{du}{dx} = \frac{2}{x}u + x^2e^x\\ x \in [1, 2],u(1) = 0 \end{array} \right. {dxdu=x2u+x2exx∈[1,2],u(1)=0
分别用Euler法,改进的Euler法,Runge-Kutta法去求解该方程,步长选为 0.1 , 0.05 , 0.01 0.1, 0.05, 0.01 0.1,0.05,0.01。画图观察求解效果。
解:本题采用4级4阶经典 R u n g e − K u t t a Runge-Kutta Runge−Kutta法,代码如下:
import numpy as np
import math
import matplotlib.pyplot as plt
def u(x):
return pow(x, 2) * (pow(math.e, x) - pow(math.e, 1))
def du_dx(x, ux):
return (2 / x) * ux + pow(x, 2) * pow(math.e, x)
def real_value(a, b, h):
t = np.arange(a + h, b + h, h)
un = [0]
for i in t:
un.append(u(i))
print("Real-Values:")
print(un)
return un
def Euler(a, b, h):
'''
:param a: 左边界
:param b: 右边界
:param h: 步长
'''
un = [0] # u(1)=0
res = 0
# 以步数划分区间,x=1除外 x=1时u=0
t = np.arange(a, b + h, h)
for i in range(len(t) - 1):
res = res + h * du_dx(t[i], un[-1])
un.append(res)
print("Euler:")
print(un)
return un
def improvedEuler(a, b, h):
'''
:param a: 左边界
:param b: 右边界
:param h: 步长
'''
un = [0] # u(1)=0
res = 0
# 以步数划分区间,x=1除外 x=1时u=0
t = np.arange(a, b + h, h)
for i in range(len(t) - 1):
tempRes = res + h * du_dx(t[i], un[-1])
res = res + (h / 2) * (du_dx(t[i], un[-1]) + du_dx(t[i + 1], tempRes))
un.append(res)
print("Improved-Euler:")
print(un)
return un
def runge_kutta(y, x, dx, f):
'''
y is un
x is tn
dx is step_length
f is du_dx
'''
k1 = f(x, y)
k2 = f(x + 0.5 * dx, y + 0.5 * dx * k1)
k3 = f(x + 0.5 * dx, y + 0.5 * dx * k2)
k4 = f(x + dx, y + dx * k3)
return y + dx * (k1 + 2 * k2 + 2 * k3 + k4) / 6.0
def cal_runge_kutta(a, b, h, y):
'''
:param a: 左边界
:param b: 右边界
:param h: 步长
:param y: u(1)=1
'''
ys, ts = [0], [1.0]
while a <= b:
y = runge_kutta(y, a, h, du_dx)
a += h
ys.append(y)
ts.append(a)
print("Runge-Kutta:")
print(ys)
return ts, ys
if __name__ == '__main__':
h = 0.1
# h = 0.05
# h = 0.01
# 存储真实结果
e0 = real_value(1.0, 2.0, h)
# 储存Euler结果
e1 = Euler(1.0, 2.0, h)
# 储存improvedEuler结果
e2 = improvedEuler(1.0, 2.0, h)
# 储存Runge-Kutta结果
ts, ys = cal_runge_kutta(1.0, 2.0, h, 0)
# 绘图横坐标
plt.plot(ts, e0, label = 'Real-Value')
plt.plot(ts, e1, label = 'Euler')
plt.plot(ts, e2, label = 'Improved-Euler')
plt.plot(ts, ys, label = 'Runge-Kutta')
# 设置横坐标的文字说明
plt.xlabel("value of x")
# 设置纵坐标的文字说明
plt.ylabel("value of u")
plt.title('h = %s' % h)
plt.legend()
plt.show()
注:步长可通过修改主函数中的 h h h进行修改。
上图选取的步长为0.1,得出的数据结果较为冗余,不在此处一一列出。通过观察图像可以得出更为简洁明确的结论:
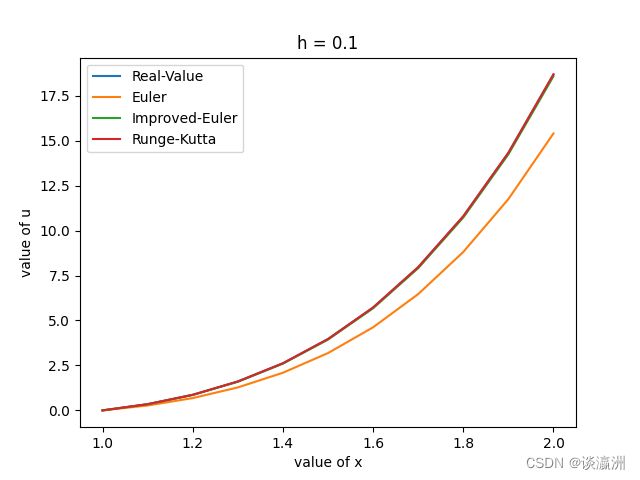
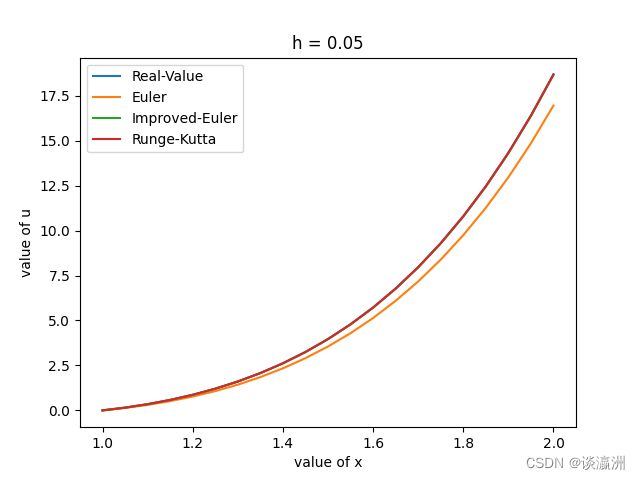
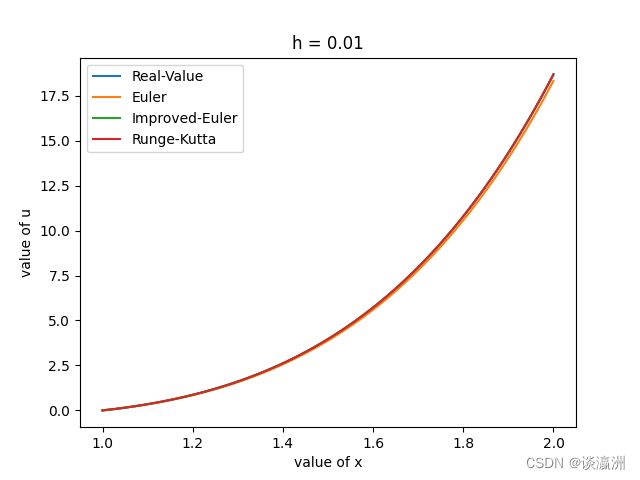
通过观察上述三幅根据不同步长得出的图像,可以看出在步长较大的时候,具有一阶精度的 E u l e r Euler Euler法得出的结果与真实值有较大出入,而改进的 E u l e r Euler Euler法和 R u n g e − K u t t a Runge-Kutta Runge−Kutta法在步长较大的时候就与真实结果十分接近;随着步长的缩小, E u l e r Euler Euler法与真实值越来越逼近,而改进的 E u l e r Euler Euler法和 R u n g e − K u t t a Runge-Kutta Runge−Kutta法始终都与真实值十分接近。