【PyTorch】实现LeNet网络的构建
【PyTorch】实现LeNet网络的构建
- 1.引入相关的包
- 2.获取数据集
- 3.搭建LeNet网络
- 4.第一次定义超参数
- 5.定义测试集的测试函数
- 6.训练网络
-
- 6.1 第二次定义超参数
- 7. 画图函数的定义
- 8.实现结果
- 参考内容
1.引入相关的包
import torch
import torchvision
import time
import matplotlib.pyplot as plt
from torch import nn,optim
from torch.utils import data # 获取迭代数据
import torchvision.datasets as mnist #获得数据集
import sys
sys.path.append('../..')
device = torch.device('cuda'if torch.cuda.is_available() else 'cpu')
device = torch.device('cuda’if torch.cuda.is_available() else ‘cpu’)
这里之所以加着这句话,是因为我们的网络是在服务器端的GPU上运行的,并非是本地。对于如何在服务器端部署pytorch,我的博客【服务器上配置pytorch】中有讲到,大家可以去参考。
2.获取数据集
我们使用的数据集仍旧是之前说的FashionMNIST衣服识别数据集,获取数据集更加详细的过程,在我的另外一个博客【实现多层感知机】上有提到。
#获取数据集
def gain_datasets(batch_size):
data_path = '../../Datasets'
data_tf = torchvision.transforms.Compose(
[torchvision.transforms.ToTensor()]
)
mnist_train = mnist.FashionMNIST(data_path,train=True,transform=data_tf,download=False)
mnist_test = mnist.FashionMNIST(data_path,train=False,transform=data_tf,download=False)
if sys.platform.startswith('win'):
num_workers = 0
else:
num_workers = 4
train_iter = data.DataLoader(mnist_train,batch_size=batch_size,shuffle=True,num_workers=num_workers)
test_iter = data.DataLoader(mnist_test,batch_size=batch_size,shuffle=True,num_workers=num_workers)
return train_iter,test_iter
此处我是将获取数据集的过程,封装到一个函数中,使得代码更加工整,这样我们思路也会更加清晰。
3.搭建LeNet网络
因为我们的这个FashionMNIST 数据集是单通道的,所以第一个卷积层的输入通道是1,如果是RGB通道的,我们就需要修改输入通道的大小为3。
#构建LeNet网络
class LeNet(nn.Module):
def __init__(self):
super(LeNet , self).__init__()
self.conv = nn.Sequential(
#in_channels,out_channels,kernel_size
nn.Conv2d(1,6,5),#因为我们的这个FashionMNIST 数据集是单通道的,所以输入通道为1
nn.Sigmoid(),
nn.MaxPool2d(2,2),
nn.Conv2d(6,16,5),
nn.Sigmoid(),
nn.MaxPool2d(2,2)
)
self.fc = nn.Sequential(
nn.Linear(16*4*4,120),
nn.Sigmoid(),
nn.Linear(120,84),
nn.Sigmoid(),
nn.Linear(84,10)
)
def forward(self,img):
feature = self.conv(img)
output = self.fc(feature.view(img.shape[0],-1))
return output
4.第一次定义超参数
net = AlexNet()
# print(net)
batch_size = 128
train_iter,test_iter = gain_datasets(batch_size,resize=224)
5.定义测试集的测试函数
我将测试集的训练单独拿出来,写到了一个函数中,为了方便大家学习参考。
def evaluate_accuracy(data_iter,net,device=None):
if device is None and isinstance(net,nn.Module):
#如果没有指定device就用net的device
device = list(net.parameters())[0].device
acc_sum,n = 0.0,0
with torch.no_grad():
for X,y in data_iter:
if isinstance(net,nn.Module):
net.eval() #进行模式评估,关闭dropout
acc_sum += (net(X.to(device)).argmax(dim=1) == y.to(device)).float().sum().cpu().item()
net.train() #改回训练模式
else:
if('is_training' in net.__code__.co_varnames): #is_training 是一个参数
acc_sum += (net(X,is_training=False).argmax(dim=1) == y).float().sum().item()
else:
acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
n += y.shape[0]
return acc_sum/n
6.训练网络
这个训练网络的函数中,包括了两个其他的函数,一个是第5节提到的,一个是画图函数。
def train_AlexNet(net,train_iter,test_iter,batch_size,optimizer,device,num_epochs):
net = net.to(device)
print("training on ",device)
loss = nn.CrossEntropyLoss()
loss_list,train_list,test_list = [],[],[]
for epoch in range(num_epochs):
train_loss_sum,train_acc_sum,n,batch_count,startTime = 0.0,0.0,0,0,time.time()
for X,y in train_iter:
X = X.to(device)
y = y.to(device)
y_hat = net(X)
l = loss(y_hat,y)
optimizer.zero_grad()
l.backward()
optimizer.step()
train_loss_sum += l.cpu().item()
train_acc_sum += (y_hat.argmax(dim=1) == y).sum().cpu().item()
n += y.shape[0]
batch_count += 1
test_acc_sum = evaluate_accuracy(test_iter,net)
loss_list.append(train_loss_sum/n)
train_list.append(train_acc_sum/n)
test_list.append(test_acc_sum)
print('epoch %d,train_loss %.4f, train_acc %.3f, test_acc %.3f, time %.1f sec'
% (epoch + 1, train_loss_sum / n, train_acc_sum / n, test_acc_sum, time.time() - startTime))
draw_function(range(1,num_epochs+1),train_list,'epochs','loss',
range(1,num_epochs+1),test_list,['train','test'])
6.1 第二次定义超参数
lr, epochs = 0.001, 10
optimizer = optim.SGD(net.parameters(), lr=lr,momentum=0.9,weight_decay=0.0005)
scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer)
train_AlexNet(net, train_iter, test_iter, batch_size, optimizer, device,epochs)
optimizer = optim.SGD(net.parameters(),lr=lr,momentum=0.9,weight_decay=0.0005)
scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer)
解释一下优化函数,我们定义的学习率为0.001,动量可以缓解过拟合的现象,此处momentum=0.9;然后就是用到的L2正则化,权重衰减为0.0005。
下面的这条语句,是对学习率在训练过程中,自动进行适当的调整。至于这个语句的具体内容,大家自行查找学习即可。
7. 画图函数的定义
该处画图函数的定义和之前的是一样,之所以画图,是因为画出来图像,更有助于我们看清楚训练的结果是否过拟合或者欠拟合。
def draw_function(x_vals, y_vals, x_label, y_label, x2_vals=None, y2_vals=None,
legend=None):
plt.title('AlexNet')
plt.xlabel(x_label)
plt.ylabel(y_label)
plt.semilogy(x_vals, y_vals,marker='o')
if x2_vals and y2_vals:
plt.semilogy(x2_vals, y2_vals, color='r',marker='o')
plt.legend(legend)
plt.show()
注意:该函数实现需要放到训练之前。
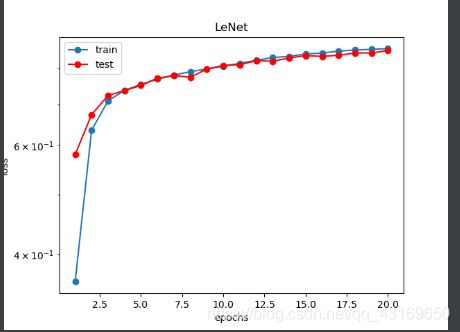
8.实现结果
每次迭代的损失率、训练精度、测试精度如下:
epoch 1, loss 0.0069, train acc 0.362, test acc 0.581, time 2.4 sec
epoch 2, loss 0.0037, train acc 0.636, test acc 0.673, time 2.2 sec
epoch 3, loss 0.0030, train acc 0.709, test acc 0.724, time 2.1 sec
epoch 4, loss 0.0027, train acc 0.737, test acc 0.736, time 2.2 sec
epoch 5, loss 0.0024, train acc 0.754, test acc 0.751, time 2.2 sec
epoch 6, loss 0.0023, train acc 0.768, test acc 0.771, time 2.1 sec
epoch 7, loss 0.0022, train acc 0.780, test acc 0.779, time 2.1 sec
epoch 8, loss 0.0021, train acc 0.790, test acc 0.774, time 2.1 sec
epoch 9, loss 0.0020, train acc 0.798, test acc 0.798, time 2.3 sec
epoch 10, loss 0.0019, train acc 0.806, test acc 0.809, time 2.2 sec
epoch 11, loss 0.0019, train acc 0.815, test acc 0.811, time 2.2 sec
epoch 12, loss 0.0018, train acc 0.824, test acc 0.823, time 2.1 sec
epoch 13, loss 0.0017, train acc 0.833, test acc 0.822, time 2.1 sec
epoch 14, loss 0.0017, train acc 0.837, test acc 0.832, time 2.1 sec
epoch 15, loss 0.0017, train acc 0.844, test acc 0.839, time 2.1 sec
epoch 16, loss 0.0016, train acc 0.847, test acc 0.837, time 2.2 sec
epoch 17, loss 0.0016, train acc 0.853, test acc 0.840, time 2.2 sec
epoch 18, loss 0.0015, train acc 0.856, test acc 0.847, time 2.1 sec
epoch 19, loss 0.0015, train acc 0.859, test acc 0.848, time 2.1 sec
epoch 20, loss 0.0015, train acc 0.861, test acc 0.855, time 2.2 sec
图像显示结果:
由图像可以看出,我们的网络拟合结果可是很好的。
参考内容
动手学深度学习pytorch实现这本书:https://tangshusen.me/Dive-into-DL-PyTorch/#/