时间序列聚类算法论文《k-Shape: Efficient and Accurate Clustering of Time Series》

ABSTRACT

  聚类是最流行的数据挖掘方法之一。这不仅仅是因为聚类问题具有很强的探索性，还因为它可以作为其他技术的预处理步骤或子过程。本文提出一种的新的时间序列聚类算法——K-shape算法。该算法依赖于一个可度量的迭代优化过程，创建同构的、分割良好的群簇。K-shape聚类算法依赖使用了规范化之后的互相关系数作为距离的度量，在每次迭代中使用它来更新聚类对聚类时间序列的分配。

1. INTRODUCTION

  聚类是应用非常广泛的一项技术，因为它不需要监督和数据标注。
  大多数时间序列分析技术，包括聚类在内，都依赖于距离测度的选择。由于无法对形状进行精准的描述，所以人们提出了几十种距离测度的方法。已有的研究表明提供振幅和相位不变性的距离测度表现非常好，所以这些距离测度被用于基于形状的聚类。
  一般认为，距离测度的选择比聚类算法本身更重要。所以，时间聚类终于依赖于经典的聚类算法，要么用更适合的实际序列的距离测度代替默认的距离测度，要把时间序列转化为平稳数据，然后使用现有的聚类算法。聚类算法的选择会影响到：(1)准确性(2)效率，也就是计算成本。
  本文提出了一种的新的时间序列聚类算法K-shape，该算法高效而且与序列的领域无关，该算法是基于一种可度量的迭代优化过程，类似于K-means算法，具体来说，K-shape使用了与K-means不同的距离测度和聚类中心的计算方法。K-shape试图在比较时间序列时保持形状，所以，K-shape需要一个对缩放和移动保持不变性的距离测度。本文展示了(1)如何推导出保持缩放不变性和唯一不变性的时间序列距离测度(2)如何有效地计算这个距离
  结果显示，我们的结果优于欧氏距离，与cDTW获得了相似的结果，而且不需要对数据做任何调整，运行速度比cDTW快了一个数量级。
&emsp: 本文认为，聚类算法的选择与距离测度的选择同样重要。

2. PRELIMINARIES

2.1 理论背景

  聚类的难度以K-means聚类为例，找到一个分割方案，使得类内的序列与聚类中心之间的距离平方和最小

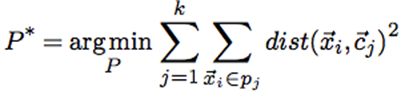
在欧氏空间中，当$k\ge 2$即使时间序列的长度为2这是一个NP-hard问题。所以K-means算法常常是去寻找局部最优解。
  K-means算法通过一个包含两个步骤的局部最优算法，第一步是分配部分，把时间序列分配到距离自己最近的聚类中心；第二步是改进部分，更新聚类中心，使聚类中心反映聚类成员的变化。算法结束的标志是算法收敛或者达到最大的迭代步数。
  Steiner’s sequence 聚类中心的计算过程就是寻找一个时间序列使得类内距离平方和最小

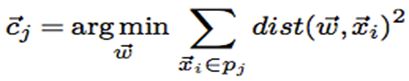
当使用欧式距离时，聚类中心的计算具有算术平均的性质。在很多情况下，需要对观测的序列进行对齐，这个问题也被称为多序列对齐问题，这个问题是NP-complete.

2.2 时间序列不变性

  缩放和转换不变性一个序列x变成$y=ax+b$，其中a和b是常数，所以y应该保持x的相似性
  平移不变性当两个序列相似但相位不同或当序列的某些区域是对齐的（局部对齐），我们可能仍然认为它们是相似地
  均匀缩放不变性长度不同的序列需要对较短的序列进行拉伸对较长的序列进行收缩，以便对其进行有效的比较。
  遮挡不变性 当缺少子序列时，仍然可以忽略不匹配的子序列进行比较
  复杂度不变性当序列具有相似的形状但不同的复杂性时，我们希望根据实际的应用场景是他们具有低或高的相似性。

2.3 时间序列距离测度

两种最先进的时间序列比较方法首先对序列进行Z归一化。最广泛使用的距离测度是欧氏距离：对于长度为m的x和y序列，得到：$$ED(x,y)=\sqrt{{\Sigma }_{i=1}^m(x_i-y_i{)}^2}$$另外一个流行的距离测度是DTW。DTW可以看作是ED的扩展，它提供了局部（非线性）对齐。用x和y中的任意两个序列的欧氏距离构造一个$m\ast m$的方阵，则“扭曲的迹”$$W=w_1,w_2,...,w_k,k\ge m$$是一组连续的矩阵元素，定义了在若干约束条件下x和y之间一种映射。$$DTW(x,y)=min\sqrt{{\Sigma }_{i=1}^k{w}_i}$$这个路径可以通过动态规划的方法进行计算，递归表达式为$$\gamma (i.j)=ED(i,j)+min\gamma (i-1,j-1),\gamma (i-1,j),\gamma (i,j-1)$$

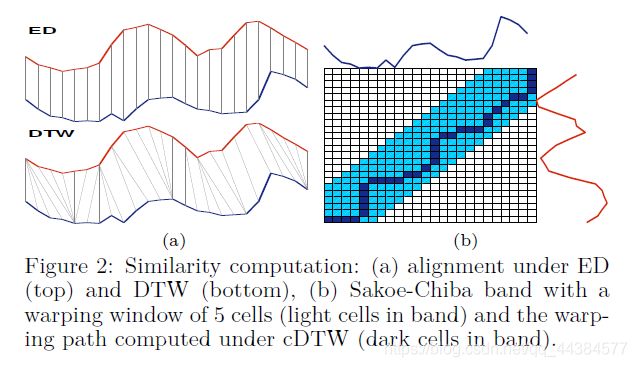
  通常的做法是该路径仅访问矩阵m上的一个单元格子集，这个子集矩阵的形状成为频带，频带的宽度称为扭曲窗口。

2.4 时间序列聚类算法

  所有的聚类算法通常会修改现有的算法，要么用更适合比较时间序列的距离测度替换默认的，要么将时间序列数据转换为扁平数据，然后用经典的算法进行解决。

2.5 聚类中心的计算

  计算聚类中心严重依赖序列之间的距离测度。这块有点复杂，以后再补。

2.6 问题的定义

  本文在给定集群个数的情况下解决了与领域无关、精确的、可度量的时间序列聚类算法。即使不同领域的数据可能需要不同的数据扭曲不变性，我们专注于采用适当的距离测度来提供序列的缩放和移动不变性。此外，为了方便的使用这种距离度量，我们重点分析未经处理的 时间序列。

3. K-shape聚类算法

  我们的目标是开发一个时间序列聚类的算法，该算法可以不受序列性质的影响，该算法中的距离测度不受序列缩放和移动的影响。具体来说，我们首先讨论距离测度，它是基于互相关的一种测度，基于这种测度我们提出了一种计算时间序列聚类中心的方法。

3.1 时间序列的形状相似

  获取形状的相似性需要能够处理振幅和相位畸变的距离测度。然而，能够满足这种要求的距离测度如DTW计算代价太大。互相关是一种对时滞信号相似度的度量，广泛应用于信号和图像处理。不正确地使用互相关，会使得它的实现像DTW一样慢，由于这些缺点，互相关没有被广泛采用作为时间序列的距离测度。
  互相关测度互相关是一种统计度量，我们可以用它来确定x和y两个序列的相似性，即使它们没有正确对齐。为了实现平移不变性，计算互相关时保持y序列不变，并将x在y上滑动，计算x的每一个位移s的内积。明确记法：$$x=(x_1,x_2,...,x_m)$$$$y=(y_1,y_2,...,y_m)$$
但考虑所有的移动时可以得出$C{C}_w(x,y)=(c_1,c_2,...,c_w)$，得到的互相关序列长度为$2m-1$，定义如下：$$C{C}_w(x,y)=R_{w-m}(x,y),w\in 1,2,...,2m-1$$$R_{w-m}(x,y)$计算方式如下：
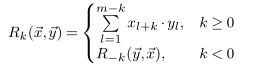
我们的目标就是计算出使得$C{C}_w(x,y)$最大的$w$。得到最优的$w$之后就可以得出x相对于y的最佳移动：$s=w-m$
  对于不同的领域或应用，可能会需要不同的归一化，最=常用的就是这三种，分别是有偏估计、无偏估计、相关系数。

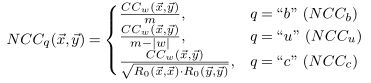
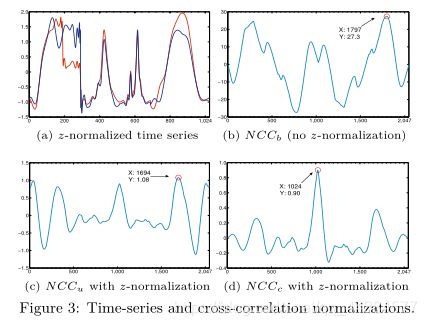
  时间序列可能还需要归一化来消除固有的畸变，图三可以看出，独立于相似度计算的归一化会影响到最终的结果。

  基于形状的距离（SBD）$$SBD(x,y)=1-ma{x}_w\left(\frac{C{C}_w(x,y)}{\sqrt{R_0(x,x)\ast R_0(y,y)}}\right)$$取值范围为$[0,2]$，0表示两个时间序列最相似
  高效计算SBD从这个式子可以看出$$C{C}_w(x,y)=R_{w-m}(x,y),w\in 1,2,...,2m-1$$可以看出$C{C}_w(x,y)$的时间复杂度是$O(m^2)$其中$m$是时间序列的长度。因为互相关的计算过程与卷积的计算过程非常类似，所以根据卷积定理，两个时间序列的卷积可以计算为单个时间序列的离散傅里叶变换（DFT）的乘积的离散傅里叶反变换(IDFT)，其中DFT为：$$F(x_k)={\Sigma }_{r=0}^{|x|-1}{x}_r{e}^{\frac{-2jrk\pi }{|x|}},k=0,1,...,|x|-1$$
IDFT：$$F^{-1}(x_r)=\frac{1}{|x|}{\Sigma }_{k=0}^{|x|-1}F(x_k)e^{\frac{2jrk\pi }{|x|}},r=0,1,...,|x|-1$$
其中$j=\sqrt{-1}$.如果一个序列在时间上首先反转180度，则互相关的计算就是两个时间序列的卷积，就相当于在频域中取复共轭（用*表示）。则
$$C{C}_w(x,y)=R_{w-m}(x,y),w\in 1,2,...,2m-1$$可以用以下的方式进行计算：$$CC(x,y)=F^{-1}\{F(x)\ast F(y)\}$$
  然而DFT和IDFT的计算仍然需要$O(m^2)$的时间。通过使用快速傅里叶变换算法，时间复杂度可以变为$O(mlog(m))$。递归算法通过将FFT划分为2的幂次块来计算FFT，因此，为了进一步提高FFT的计算性能，当$CC(x,y)$不是精确的2的幂时，我们可以在x和y之间填充0使得在$2m-1$之后依然是的2的幂次的长度。
  算法的流程如下：

3.2 时间序列形状提取

  时间序列分析中的许多任务依赖于通过一个序列有效地总结一组时间序列的方法。这个摘要序列通常被称为平均序列，或者，在聚类中，被称为质心。
  从一组序列中提取平均序列的最早的方法是计算所有序列对应坐标的算术平均值作为平均序列。K-means算法就是采用的这种方式。图4可以看出这种方式计算的质心没有很好地捕捉这类序列的特征。

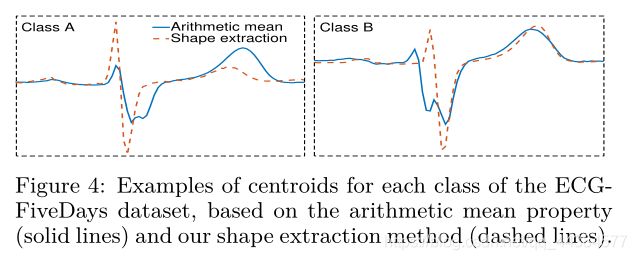
  为了避免这种问题，我们把质心计算视为一个优化问题，其目标是找到与类内所有其他时间序列之间距离平方和的最小值。因此就变为一个优化问题：$${\mu }_k=argma{x}_{{\mu }_k}{\Sigma }_{x_i\in P_k}NC{C}_c(x_i,{\mu }_k{)}^2=argma{x}_{{\mu }_k}{\Sigma }_{P_k}{\left(\frac{ma{x}_{w}C{C}_w(x_i,{\mu }_k)}{\sqrt{R_0(x_i,x_i).R_0({\mu }_k,{\mu }_k)}}\right)}^2$$
  该式需要对类内所有的时间序列计算一个最佳的偏移。因为我们在这里提到的方法是用在迭代聚类当中，所以我们把前一次计算得到的聚类中心作为参考并把所有的序列与这个参考的序列对齐。把前一次的聚类中心作为参考是合理的，m
省略上式的分母得到：$${\mu }_k=argma{x}_{{\mu }_k}{\Sigma }_{x_i\in P_k}\left({\Sigma }_{l\in [1,m]}{x}_{il}.{\mu }_{kl}\right)$$
为了简单起见，我们用向量表示此方程，并假设序列已经进行了Z归一化处理序列的振幅差。得到：
$${\mu }_k=argma{x}_{{\mu }_k}{\Sigma }_{x_i\in P_k}(x_i^T.{\mu }_k{)}^2=argma{x}_{{\mu }_k}{\mu }_k^T.{\Sigma }_{x_i\in P_k}(x_i.x_i^T).{\mu }_k$$
在上面的式子中，我们没有对${\mu }_k$进行Z正则化。为了归一化数据，我们令${\mu }_k={\mu }_k.Q$，其中 $Q=I-\frac{1}{m}O$，其中I是单位矩阵，O是全幺矩阵，用S代替${\Sigma }_{x_i\in P_k}(x_i.x_i^T)$，可以得到：$${\mu }_k=argma{x}_{{\mu }_k}\frac{{\mu }_k^T.Q^T.S.Q.{\mu }_k}{{\mu }_k^T.{\mu }_k}=argma{x}_{{\mu }_k}\frac{{\mu }_k^T.M.{\mu }_k}{{\mu }_k^T.{\mu }_k}$$
其中$M=Q^T.S.Q$
最新的${\mu }_k$求解是一个著名的Rayleigh Quotient最大化问题。我么可以找到最大值${\mu }_k$作为特征向量，它对应于实对称矩阵M的最大特征值。算法二展示了如何提取最具代表性的序列形状。

3.3 基于形状的时间序列聚类

  我们提出的算法可以在保证缩放不变性、平移不变性和转换不变性的同时高效地比较序列和计算序列中心。在每次迭代中，K-shape算法执行两个步骤：(1)在分配步骤中，算法通过将每个时间序列 与所有计算出地质心进行比较，并将每个时间序列分配给最接近质心地聚类来更新聚类中的成员关系; (2)在细化步骤中，更新聚类中心以反映前一步中聚类成员的变化。算法重复这两个步骤，直到集群成员没有变化，或者达到允许的最大迭代次数。在赋值步骤中，算法主要依赖于3.1中的距离测度，在细化步骤中，主要依赖于聚类中心的计算方法。
  时间复杂度$n$表示时间序列的个数，$k$是集群的个数，$m$是时间序列的长度。在分配步骤中，聚类算法利用SBD计算n个时间序列到k个聚类中心的相似性，需要时间为$O(m.log(m))$，所以这一步的时间复杂度就是$O(n.k.m.log(m))$。在每一个集群的细化步骤中，聚类算法计算矩阵M，需要$O(m^2)$的时间，对M执行特征值分解，需要$O(m^3)$的时间。所以这一步的总时间为$O(max\{n.m^2,k.m^3\})$。所以，总的来说K-shape算法每次迭代需要的时间复杂度为$O(max\{n.k.m.log(m),n.m^2,k.m^3\})$。可以看出该算法的时间复杂度与时间序列的数量有现行的关系，大部分的计算代价取决于时间序列的长度。但是时间序列的长度通常比时间序列的数量小得多，因此对m的依赖并不是瓶颈。在m非常大的情况下，可以使用分割或降维的方法来充分减少序列的长度。
K-shape算法：