Lasso线性回归学习笔记（公式与代码实现）

Lasso线性回归学习笔记（公式与代码实现）

1 为什么要在线性回归中引入正则化项（简介）

 （主要参考《机器学习》周志华 第三章）

首先，多元线性回归的基本形式为$f(x\text{x}x)={w\text{w}w}^{T}x\text{x}x+b$，为便于讨论，把 $w\text{w}w$ 和 $b$ 吸收入向量形式 $\widehat{w\text{w}w}=(w\text{w}w;b)$，相应的，把数据集 $D$ 表示为一个 $m\times (d+1)$ 大小的矩阵 $X\text{X}X$ （其中$m$为样本条数，$d$为特征数），即
$$X\text{X}X=\left(\begin{array}{ccccc}{x}_{11}& x_{12}& \cdots & x_{1d}& 1\\ x_{21}& x_{22}& \cdots & x_{2d}& 1\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ x_{m1}& x_{m2}& \cdots & x_{md}& 1\end{array}\right)$$
再把标记也写成向量形式 $y=(y_1;y_2;\cdots ;y_m)$，
则根据最小二乘法，参数估计值${\widehat{w\text{w}w}}^{\ast }$应该满足
$${\widehat{w\text{w}w}}^{\ast }=\underset{\hat{w}}{\mathrm{argmin}}(y\text{y}y-X\text{X}X\widehat{w\text{w}w}{)}^T(y\text{y}y-X\text{X}X\widehat{w\text{w}w})$$
令 $E_{\hat{w}}=(y\text{y}y-X\text{X}X\widehat{w\text{w}w}{)}^T(y\text{y}y-X\text{X}X\widehat{w\text{w}w})$,对$\widehat{w\text{w}w}$求导得到（相关矩阵求导知识链接）

$$\frac{\partial E_{\hat{w}}}{\partial \hat{w}}=2{X\text{X}X}^T(X\text{X}X\widehat{w\text{w}w}-y\text{y}y)$$

令上式得零则可得到 $\widehat{w\text{w}w}$ 的最优解，有两种情况：

• 情况一：当 ${X\text{X}X}^{T}X\text{X}X$ 为满秩矩阵时，即可逆，令上式得零，可直接通过移项求的
  $${\widehat{w\text{w}w}}^{\ast }=({X\text{X}X}^{T}X\text{X}X{)}^{-1}{X\text{X}X}^{T}y\text{y}y$$
• 情况二：然而现实任务中 ${X\text{X}X}^{T}X\text{X}X$ 往往不是满秩矩阵，例如在高维数据中，变量的数目会超过样例数目，导致 $X\text{X}X$ 的列数多于行数，而 ${X\text{X}X}^{T}X\text{X}X$ 秩等于 $X\text{X}X$ 的秩，显然${X\text{X}X}^{T}X\text{X}X$ 不满秩，此时可解出多个 $\widehat{w\text{w}w}$ (个人参考了《2022张宇线代9讲》P29 矩阵方程)，它们都能使均方误差最小化，选择哪一个作为输出，常见的做法是引入正则化（regularization）项。

2 常见正则化项

首先介绍常见范数——P-范数 (范数详见百度百科)，即
$$||x\text{x}x|{|}_p=(|x_1{|}^p+|x_2{|}^p+\cdots +|x_n{|}^p{)}^{\frac{1}{p}}$$
L₁范数正则化项，即令 $p$ = 1,并针对参数向量，即为 $\lambda ||w\text{w}w|{|}_1$ ,其中 $\lambda$ 为正则化参数。对于 L₁ 正则化， $\lambda$ 越大可以使越多的参数为零或接近零。

类似地，L₂范数正则化项为 $\lambda ||w\text{w}w|{|}_2^2$

3 损失函数图像与正则化之后的图像

（参考文章链接，下面是利用网站GeoGebra画出的函数图像）

3.1损失函数图像

为了可视化，假设一个回归函数及相应的损失函数如下：
回归函数：$f(x_i)=w_1{x}_i+b$
损失函数（均方差）：$L=\frac{1}{m}\sum _{i=1}^m(f(x_i)-y_i{)}^2$其中m表示样本量，

为了保持简单，只取一个样本点(1,1)代入上面的代价函数方程中，即 $L=(w_1+b-1{)}^2$
以下则是上式的图像

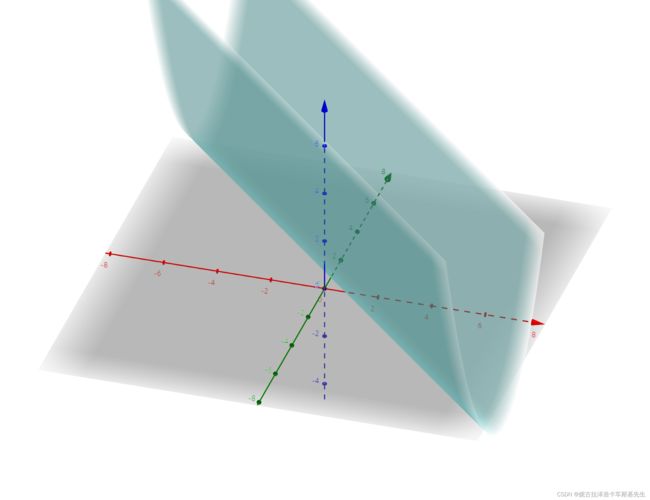
可以看出，有无穷多个解可以使损失函数达到最小值。根据前面的论证，在只有一个样本点情况下，外加上最后一列是 1，得到的反应数据集 $D$ 的矩阵 $X\text{X}X$是一行两列，${X\text{X}X}^{T}X\text{X}X$ 不是满秩矩阵，解不唯一，没毛病。

3.2 加了 L₁ 正则项之后的损失函数图像

加了 L₁ 正则项之后的损失函数： $L=w_1+b-1+|w_1|$ （令$\lambda =1$）
上式图像为

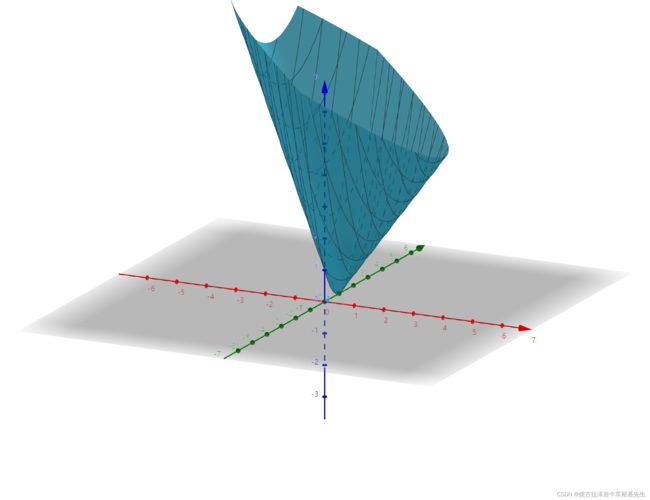
可以看出，有唯一最优解了

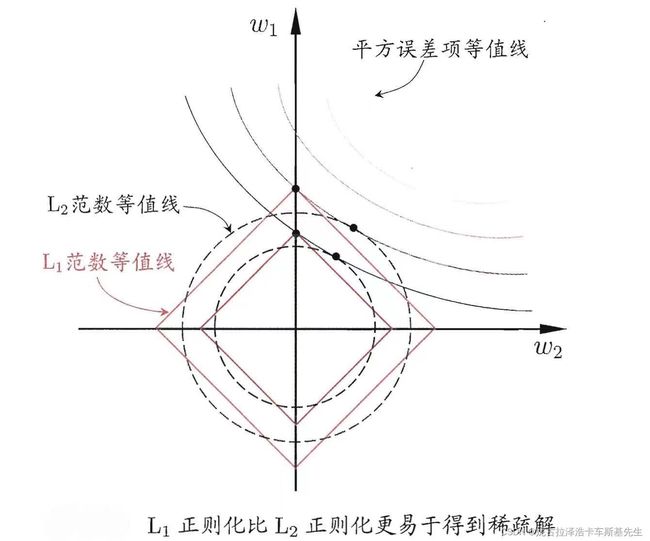
4 L₁ 范数正则化的解中有更多零的原因

(《机器学习》周志华 p253)

经典图片了，不多说了。

5 Lasso 线性回归

就是在损失函数中加入 L₁正则化项的线性回归，值得注意的是在测试集中验证预测效果的时候的损失函数是不带正则化项的。

6 Lasso线性回归的优化算法（求最优解）

6.1 梯度下降（Gradient Descent）

- 为什么梯度方向是函数上升最快方向？

(参考：为什么梯度反方向是函数下降最快的方向？、《2022张宇高数18讲（第17讲）》)

首先介绍经典的梯度下降算法。
可能都知道，梯度下降算法的迭代公式是
$${\widehat{w\text{w}w}}^{k+1}={\widehat{w\text{w}w}}^k-\eta \frac{\partial L({\widehat{w\text{w}w}}^k)}{\partial \widehat{w\text{w}w}}$$
其中 $\widehat{w\text{w}w}=(w\text{w}w;b)$，而
$$\frac{\partial L({\widehat{w\text{w}w}}^k)}{\partial \widehat{w\text{w}w}}$$
便是优化目标中的损失函数 $L(\widehat{w\text{w}w})$ 的梯度，接下来只要弄清为什么梯度方向是函数上升最快的方向，便就清楚这个式子了。

- 向量的方向角和方向余弦

（1）非零向量 $a\text{a}a$ 与 $x$ 轴、$y$ 轴、$z$ 轴正向的夹角 $\alpha$、$\beta$、$\gamma$ 称为 $a\text{a}a$ 的方向角。
（2） $cos\alpha$、$cos\beta$、$cos\gamma$ 称为 $a\text{a}a$ 的方向余弦，且$cos\alpha =\frac{a_x}{|a|}$、$cos\beta =\frac{a_y}{|a|}$、$cos\gamma =\frac{a_z}{|a|}$
（3）由（2）可知$\frac{a}{|a|}=(cos\alpha ，cos\beta ，cos\gamma )$ 称为向量 $a\text{a}a$ 的单位向量
以上基础知识有利于从二元直接向更多元推广。

- 方向导数

要想解决以上疑问，首先要知道方向导数。在许多问题中，不仅要知道函数在坐标轴方向上的变化率（即偏导数），而且还要设法求得函数在某点沿着其他特定方向上的变化率。这就是方向倒数。

• 首先给出明确定义：(此部分我感觉参考文章写的更好理解，以下定义更精确、好推广)
  设二元函数 $u=u(x,y)$在点 $P_0(x_0,y_0)$ 有定义，$l$ 为从 $P_0$ 出发的射线，$P(x,y)$ 为在 $l$ 上的任一点，则
  $$\{\begin{array}{r}x-x_0=\Delta x=tcos\alpha \\ y-y_0=\Delta y=tcos\beta \end{array}$$
  其中 $t=\sqrt{(\Delta x{)}^2+(\Delta y{)}^2}$ 表示 $P$ 与 $P_0$ 之间的距离。
  则极限
  $$\begin{gathered} \underset{t\to 0^{+}}{\lim }\frac{u(P)-u(P_0)}{t} \\ =\underset{t\to 0^{+}}{\lim }\frac{u(x_0+tcos\alpha ,y_0+tcos\beta )-u(x_0,y_0)}{t} \end{gathered}$$
  此极限便是函数 $u$ 在点 $P_0$ 沿方向 $l\text{l}l$ 的方向导数，记作
  $$\frac{\partial u}{\partial l\text{l}l}{|}_{P_0}$$

• 方向导数计算公式：设函数 $u=u(x,y)$ 在点 $P_0$ 点出可微分，则 $u$ 在点 $P_0$ 处沿任意方向 $l\text{l}l$ 的方向导数都存在，且
  $$\begin{array}{rl}\frac{\partial u}{\partial l\text{l}l}{|}_{P_0}=& \underset{t\to 0^{+}}{\lim }\frac{u(P)-u(P_0)}{t}\\ =& \underset{t\to 0^{+}}{\lim }\frac{u(x_0+\Delta x,y_0+\Delta y)-u(x_0,y_0)}{\sqrt{(\Delta x{)}^2+(\Delta y{)}^2}}\\ \stackrel{\ast }{=}& \underset{t\to 0^{+}}{\lim }\frac{u_x^{\prime }(P_0)\Delta x+u_y^{\prime }(P_0)\Delta y+o(t)}{\sqrt{(\Delta x{)}^2+(\Delta y{)}^2}}\\ =& u_x^{\prime }(P_0)cos\alpha +u_y^{\prime }(P_0)cos\beta \end{array}$$
  其中 $cos\alpha$、$cos\beta$ 为方向 $l\text{l}l$ 的方向余弦，$\stackrel{\ast }{=}$ 部分利用的多元函数的泰勒展开式

-方向导数与梯度的关系

从上式可以看出，方向导数其实就是 梯度 $grad\text{grad}gradu=(u_x^{\prime },u_y^{\prime })$ 与 方向余弦组成的单位向量 $I=(cos\alpha ,cos\beta )$ 的内积，即
$$\frac{\partial u}{\partial l\text{l}l}=grad\text{grad}gradu\cdot I=|grad\text{grad}gradu||I|cos\theta =|grad\text{grad}gradu|cos\theta$$
其中 $\theta$ 为两向量之间的夹角。

那么如果此时想让 $\frac{\partial u}{\partial l\text{l}l}$ 最大，自然是 $\theta$ 为 $0^o$ 的时候，也就是方向与梯度一致的时候的方向导数最大，即变化率最大且是正的，那么如果沿着该方向前进，可以上升（增加）的最快；同理，如果$\theta$ 为 $180^o$ 的时候，也就是方向与梯度相反的时候的方向导数最小且为负（两者的绝对值相同），那么沿着该方向前进就可以下降（减小）的最快。

【注】以上证明角度最直观好想，对于梯度下降算法的证明还有其他角度，例如在一定条件下直接利用泰勒展开近似目标函数，然后直接求解，得到的就是梯度下降迭代式，在下文中的近端梯度下降其实就利用到了这个思想。

6.2 近端梯度下降（Proximal Gradient Descent）

参考文章（
近端梯度下降法，
《机器学习》（周志华）P253，
《机器学习公式详解》（俗称南瓜书）P122（pdf页数），
矩阵微分与向量函数泰勒展开）

近端梯度下降法是众多梯度下降 (gradient descent) 方法中的一种，将proximal翻译成“近端”可能是想表达 “接近，近似” 的意思，但在这点上，经典梯度算法其实也是近似的。与经典的梯度下降法相比，近端梯度下降法 主要是想解决目标函数中存在不可微或不方便微分的部分。如对于凸优化问题，当其目标函数存在 L₁正则化项，近端梯度下降法就会派上用场。
（个人理解：其实就是在经典梯度下降的基础上，最后用分段函数的方法对L₁正则化项求导）

具体来说，设优化目标
$$minf(x\text{x}x)+\lambda ||x\text{x}x|{|}_1$$
令 $\nabla$ 表示微分算子，$\nabla f(x\text{x}x)$ 即为 $\frac{\partial f(x)}{\partial x}$（$x$ 为向量，粗的打不出来了）

- 大致思想

（1）在一定条件下，通过泰勒展开式将目标函数可微的部分化简
（2）以分段函数的形式，对 $||x\text{x}x|{|}_1$ 求导，令导数得零，最后自然得到了分段函数形式的迭代公式 (加粗的是向量)。

- 推导过程

 
L-Lipschitz 条件简介：它是一个比“连续”更强的光滑性条件.直觉上，利普希茨连续函数限制了函数改变的速度，符合利普希茨条件的函数的斜率，必小于一个称为利普希茨常数的实数 L（该常数依函数而定，在梯度下降中，可以将此参数理解为学习率 $\eta$ 的倒数，在训练中应该自己给出）（以上仅为个人理解，详见百度百科）
 
若 $f(x\text{x}x)$ 可导，且 $\nabla f(x\text{x}x)$满足 L-Lipschitz 条件，即存在常数 $L>0$ 使得
$$\frac{|\nabla f({x\text{x}x}^{\prime })-\nabla f(x\text{x}x)|}{|{x\text{x}x}^{\prime }-x\text{x}x|}\le L$$
(上式可看成是 $f(x\text{x}x)$ 的二阶导数恒不大于 $L$ ，即 ${\nabla }^{2}f(x\text{x}x)\le L$ )
则在 $x_k$ 附近可将 $f(x)$ 通过二阶泰勒展开式近似为
$$\begin{array}{rl}\widehat{f(x\text{x}x)}\approx & f({x\text{x}x}_k)+(\nabla f({x\text{x}x}_k),(x\text{x}x-{x\text{x}x}_k))+\frac{{\nabla }^{2}f(x_k)}{2}||x\text{x}x-{x\text{x}x}_k|{|}_2^2\\ \le & f({x\text{x}x}_k)+(\nabla f({x\text{x}x}_k),(x\text{x}x-{x\text{x}x}_k))+\frac{L}{2}||x\text{x}x-{x\text{x}x}_k|{|}_2^2\\ =& \frac{L}{2}||x\text{x}x-({x\text{x}x}_k-\frac{1}{L}\nabla f({x\text{x}x}_k))|{|}_2^2+const\end{array}$$
其中 $const$ 是与 $x\text{x}x$ 无关的常数（后续的求解过程也是求导，就直接忽略了，上述具体推导过程参见《机器学习公式详解》（俗称南瓜书）第11章）
也就是说在 ${x\text{x}x}_k$ 附近可将目标函数进行简化，那么问题可转化为在这个小范围内寻找可使目标函数最小的 ${x\text{x}x}_{k+1}$，然后再进行迭代（对于经典梯度下降算法来说，其实也是这么个思想），即
$${x\text{x}x}_{k+1}=\underset{x}{\mathrm{argmin}}\frac{L}{2}||x\text{x}x-({x\text{x}x}_k-\frac{1}{L}\nabla f({x\text{x}x}_k))|{|}_2^2+\lambda ||x\text{x}x|{|}_1$$
令 $x^i$ 表示 $x\text{x}x$ 的第 $i$ 个分量，将上式按分量展开可看出，其中不存在 $x^i{x}^j(i\ne j)$ 这样的项，也就是说各分量直间互不影响，假设只有一个分量 $x^1$ 带入展开，求导，令导得零，便可以求得这个小范围内的最小值点，推广可得上式解为：
可先计算 $z\text{z}z={x\text{x}x}_k-\frac{1}{L}\nabla f({x\text{x}x}_k)$
$$x_{k+1}^i=\{\begin{array}{rlrl}{z}^i& -\lambda /L,& \lambda /L& <z^i\\ 0& ,& |z^i|& \le \lambda /L\\ z^i& +\lambda /L,& z^i& <-\lambda /L\end{array}$$
(如果不考虑 L₁ 正则化项，该步骤得解就是 经典梯度下降 的迭代公式)

7 代码实现

import numpy as np

# 导入数据
filepath = "D:\\机器学习\\housing.csv"
data = np.loadtxt(filepath, delimiter=',', skiprows=1, encoding='utf-8')
# 选择特征与标签
x = data[0:20, 1:]
y = data[0:20, 0]
# 加一列
X = np.column_stack((x, np.ones((x.shape[0], 1))))
# 划分训练集与测试集
X_train, y_train = x[:10], y[:10]
X_test, y_test = x[10:], y[10:]

print(X_train.shape, y_train.shape, X_test.shape, y_test.shape)


# 定义初始化参数
def initialize(dims):
    w = np.zeros((dims))
    return w


# 在 MSE 基础上定义 Lasso 损失函数值

def l1_loss(X, y, w, lambda_):
    num_train = X.shape[0]
    y_hat = np.dot(X, w)
    loss = np.sum((y_hat - y) ** 2) / num_train + np.sum(lambda_ * abs(w))

    return y_hat, loss, num_train


# 定义训练过程

def lasso_train(X, y, learn_rate=50, lambda_=50, epochs=300):
    loss_list = []
    w = initialize(X.shape[1])
    temporary_para = lambda_ * learn_rate

    for i in range(epochs):
        y_hat, loss, num_train = l1_loss(X, y, w, lambda_)
        z = w - learn_rate * (np.dot(X.T, (y_hat - y)) * 2 / num_train)
        a = np.dot(X.T, (y_hat - y))
        b = X.T
        c = (y_hat - y)
        y_hat[0]

        w_list = []
        for z_i in z:
            if z_i > temporary_para:
                w_i = z_i - temporary_para

            elif z_i < temporary_para:
                w_i = z_i + temporary_para

            else:
                w_i = 0

            w_list.append(w_i)

        w = np.array(w_list)
        loss_list.append(loss)

        if i % 50 == 0:
            print('epoch %d loss %f' % (i, loss))
        params = w

    return loss, loss_list, params


loss, loss_list, params = lasso_train(X,
                                      y,
                                      learn_rate=50,
                                      lambda_=50,
                                      epochs=300)