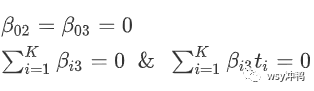b样条和三次样条_回归样条入门
1. 为什么需要样条回归?
线性模型:
逻辑回归:
Cox回归:
这些常用模型的最基础的假设就是因变量的变形和协变量线性相关,而这个假设是有问题的。人们通常对连续协变量分组,然后使用一些虚拟变量来解决这个问题,但是这样做也有不好的地方:1.把连续协变量分组成数个无序变量,会损失信息;2.这样做有些随意,而且如果是极端暴露(如重度营养不良等)和因变量有关系,那么根据quartile分组会掩盖这一关系,甚至产生误导。
上述问题也可以用多项式回归:
但是低阶多项式对非线性关系的解释力度不够,高阶的会因为数据的异常值而拟合出非常怪异的曲线,因此多项式回归也不是一个那么好的办法。
2. 基函数,回归样条,光滑样条
基函数
分段多项式
例子:
而这样的分段多项式一般是不连续的,因为是分块拟合的。因此我们通常需要对分段多项式加一些限制。比如要求在x=c时左右相等,一阶与二阶导数相等,这样的拟合曲线更符合常理。
Rmk:d阶样条的一般定义是分段d阶多项式,同时每个节点直到d-1阶导数都是连续的。(这样并不轻松!)
节点(Knot)
一次样条
直接copy的书上的代码,不过不难理解
pred7 5)*(age>=5)) + I((age-10)*(age >= 10)) + I((age-20)*(age >= 20)) + I((age-30)*(age >= 30)) + I((age-40)*(age >= 40)),data = triceps))
ggplot(triceps, aes(x=age, y=triceps)) +
geom_point(alpha=0.55, color="black") +
theme_minimal() +
geom_line(data=triceps,aes(y = pred7, x=age), size = 1, col="blue")立方样条
对数据集拟合有K个节点的三次样条,我们使用如下形式:
更一般地,我们指定:
则样条函数为:
含有K+n+1个回归系数,其中n为阶数,K为节点数(相当于生成了K+n个新变量用于回归)。使用OLS或者极大似然可以估计出所有的系数。可以证明在每个节点,函数本身、一阶导数和二阶导数都是连续的。
限制性立方样条
不妨设K个节点分别为t1
限制性立方样条的定义:
S(x)在x,且S(x)在x 把条件带入+上式展开,有: 相当于生成了K-2个新变量: 那么非线性的显著程度(Significance of Non-linearity)可以通过比较这个K-2个新变量的模型和协变量的线性模型的log-likelihood。(然后我记得两个模型的likelihood进过一定变形后会服从卡方分布)。 系数的95%CI也是用常规的方法计算: 节点的选择 常规的话节点的位置通常是{5%,50%,95%},{5%,25%,75%,95%},{5%,25%,50%,75%,95%},而不怎么讲道理的方法是尝试不同的节点数和节点位置,选择拟合形状理想的曲线,客观一些的方法是做交叉验证,记录不同节点数、节点位置下的均方误差,然后再根据一定规则(例如:某一结点的均方误差的error bar包含了最低的均方误差在内,且该节点数较少) 更换节点位置: R语言实现限制性立方样条(简易) 光滑样条 为了对给定的数据拟合光滑曲线,实际上是要找到某个函数g(x),使得他能很好地拟合观测数据,也就是: 这样会导致严重的过拟合问题,因为如果不对g(x)做任何限制,则只能得到一个取值为0的RSS,g在每个yi处插值即可。 保证g光滑,最小化: 二阶导数对应斜率的变化程度,衡量函数的“粗糙度”。g越光滑,惩罚项越小。 λ的选择则可以通过交叉验证进行。 局部回归与广义可加模型GAM 下次一定! 应用回归样条的文献(供参考) Jieli Lu, Jiang He, Mian Li, et al. Predictive Value of Fasting Glucose, Postload Glucose, and Hemoglobin A1c on Risk of Diabetes and Complications in Chinese Adults. Diabetes Care 2019. 参考文献 SYLVAIN DURRLEMAN AND RICHARD SIMON, FLEXIBLE REGRESSION MODELS WITH CUBIC SPLINES, STATISTICS IN MEDICINE, VOL. 8, 551-561 (1989) 不记得从哪里下载的一篇文章 Jaroslaw Harezlak & Armando Teixeira-Pinto, Machine Learning for Biostatistics Module 5 Sander Greenland, Dose-Reponse And Trend Analysis, Epidemiology, VOL. 6, 356-365(1995) Gareth James, et al, An Introduction to Statistical Learning with Applications in R, Springer, 2015.ddist=datadist(data) #data为生存数据,包括状态,生存时间,主要因变量,协变量
options(datadist='ddist')
fit=cph(Surv(interval, status)~rcs(main_VAR,4)+co_VAR,data = data)
ddist$limits$main_VAR[2]=NUM #指定HR=1的点
fit=update(fit)
HR=Predict(fit,main_VAR,fun=exp,ref.zero = T)
anova(fit) #查看非线性效应是否显著
#画图(自己刚刚用过的)
ggplot()+
geom_ribbon(data = HR,aes(x=main_VAR,ymin = lower, ymax = upper),
alpha = 0, linetype = 2, colour="#4103ED")+
geom_line(data=HR,aes(x=main_VAR,y = yhat), colour = "#4103ED")+
theme_classic() +
theme(panel.grid = element_blank(),
legend.position = "top", # legend 置顶
panel.border = element_blank(),
plot.title = element_text(hjust = 0.5)) + # 标题居中
labs(x = "main_VAR", y = "Adjusted HR", title = "Association between main_VAR and Survival",
color = "", fill = "")+
theme(axis.title.x = element_text(size = 15))+ #调整字和刻度的大小
theme(axis.title.y = element_text(size = 15))+
theme(axis.text.x = element_text(size = 12))+
theme(axis.text.y = element_text(size = 12))+
geom_abline(intercept = 1,slope = 0,linetype=1)+
annotate("text", x=7.5, y=8, label="P for non-linear trend = NUM", alpha=1,size=4.5) #图上加文字