【超全面】机器学习中的超参优化方法总结

目录

1. 什么是超参数

2. 超参数类型

3. 主流超参优化方法

（1）手动调参

缺点:

python代码：（例子）

手动调参 参数的重要性顺序

超参具体如何影响模型性能

超参合适的范围

（2）网格搜索

缺点：

python代码： 

（3）随机搜索

缺点： 

python代码：

（4）贝叶斯搜索

 缺点：

python代码：

3. 新型超参优化方法--VeLO

如何打造AI优化器？        

新型优化器评价

---

1. 什么是超参数

超参数是在建立模型时用来控制算法行为的参数。这些参数不能从正常的训练过程中学习。他们需要在训练模型之前被分配。

百度的超参数的定义：

在机器学习的上下文中，超参数是在开始学习过程之前设置值的参数，而不是通过训练得到的参数数据。通常情况下，需要对超参数进行优化，给学习机选择一组最优超参数，以提高学习的性能和效果

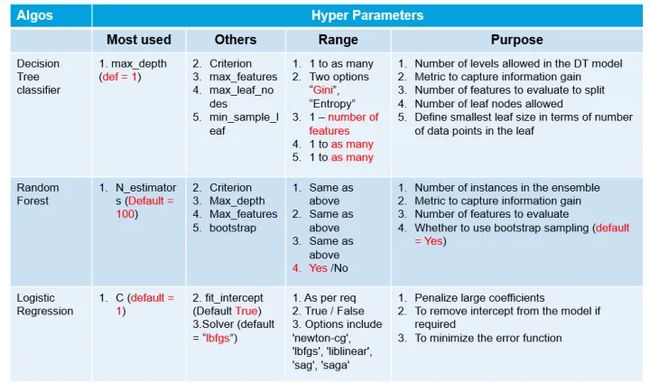
Dr.Mukesh Rao的超参数样本清单 

2. 超参数类型

神经网络的超参数主要分为2种：

1）网络结构相关：网络中间层数量、类型（全连接、丢弃层、归一化层、卷积层等）、每层神经元数量、激活函数等

2）模型训练相关：损失函数、优化方法、批次大小、迭代次数、学习率、正则方法和系数、初始化方法等

3. 主流超参优化方法

（1）手动调参

自己定义参数的范围，然后反复试验进行调整。

缺点:

1. 不能保证得到最佳的参数组合。
2. 耗时费力。

python代码：（例子）

#importing required libraries
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold , cross_val_score
from sklearn.datasets import load_wine

wine = load_wine()
X = wine.data
y = wine.target

#splitting the data into train and test set
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size = 0.3,random_state = 14)

#declaring parameters grid
k_value = list(range(2,11))
algorithm = ['auto','ball_tree','kd_tree','brute']
scores = []
best_comb = []
kfold = KFold(n_splits=5)

#hyperparameter tunning
for algo in algorithm:
  for k in k_value:
    knn = KNeighborsClassifier(n_neighbors=k,algorithm=algo)
    results = cross_val_score(knn,X_train,y_train,cv = kfold)

    print(f'Score:{round(results.mean(),4)} with algo = {algo} , K = {k}')
    scores.append(results.mean())
    best_comb.append((k,algo))

best_param = best_comb[scores.index(max(scores))]
print(f'\nThe Best Score : {max(scores)}')
print(f"['algorithm': {best_param[1]} ,'n_neighbors': {best_param[0]}]")

手动调参 参数的重要性顺序

•  学习率

在网络参数、优化参数、正则化参数中最重要的超参数可能就是学习率了。学习率直接控制着训练中网络梯度更新的量级，直接影响着模型的有效容限能力；

• 损失函数上的可调参数

损失函数上的可调参数，这些参数通常情况下需要结合实际的损失函数来调整，大部分情况下这些参数也能很直接的影响到模型的的有效容限能力。

这些损失一般可分成三类：

第一类，辅助损失结合常见的损失函数，起到辅助优化特征表达的作用。例如度量学习中的Center loss，通常结合交叉熵损失伴随一个权重完成一些特定的任务。这种情况下一般建议辅助损失值不高于或者不低于交叉熵损失值的两个数量级；

第二类，多任务模型的多个损失函数，每个损失函数之间或独立或相关，用于各自任务，这种情况取决于任务之间本身的相关性，目前笔者并没有一个普适的经验由于提供参考；

第三类，独立损失函数，这类损失通常会在特定的任务有显著性的效果。例如RetinaNet中的focal loss，其中的参数γ，α，对最终的效果会产生较大的影响。这类损失通常论文中会给出特定的建议值。

• 批样本数量，动量优化器（Gradient Descent with Momentum）的动量参数β。

批样本决定了数量梯度下降的方向。过小的批数量，极端情况下，例如batch size为1，即每个样本都去修正一次梯度方向，样本之间的差异越大越难以收敛。若网络中存在批归一化（batchnorm），batch size过小则更难以收敛，甚至垮掉。这是因为数据样本越少，统计量越不具有代表性，噪声也相应的增加。而过大的batch size，会使得梯度方向基本稳定，容易陷入局部最优解，降低精度。一般参考范围会取在[1:1024]之间，当然这个不是绝对的，需要结合具体场景和样本情况；

动量衰减参数β是计算梯度的指数加权平均数，并利用该值来更新参数，设置为 0.9 是一个常见且效果不错的选择；

• Adam优化器的超参数、权重衰减系数、丢弃法比率（dropout）和网络参数。

这些参数在大部分实践中不建议过多尝试，例如Adam优化器中的β1，β2，ϵ，常设为 0.9、0.999、10−8就会有不错的表现。

权重衰减系数通常会有个建议值，例如0.0005 ，使用建议值即可，不必过多尝试。

dropout通常会在全连接层之间使用防止过拟合，建议比率控制在[0.2,0.5]之间。

使用dropout时需要特别注意两点：

一、在RNN中，如果直接放在memory cell中,循环会放大噪声，扰乱学习。一般会建议放在输入和输出层；

二、不建议dropout后直接跟上batchnorm，dropout很可能影响batchnorm计算统计量，导致方差偏移，这种情况下会使得推理阶段出现模型完全垮掉的极端情况；

网络参数通常也属于超参数的范围内，通常情况下增加网络层数能增加模型的容限能力，但模型真正有效的容限能力还和样本数量和质量、层之间的关系等有关，所以一般情况下会选择先固定网络层数，调优到一定阶段或者有大量的硬件资源支持可以在网络深度上进行进一步调整。

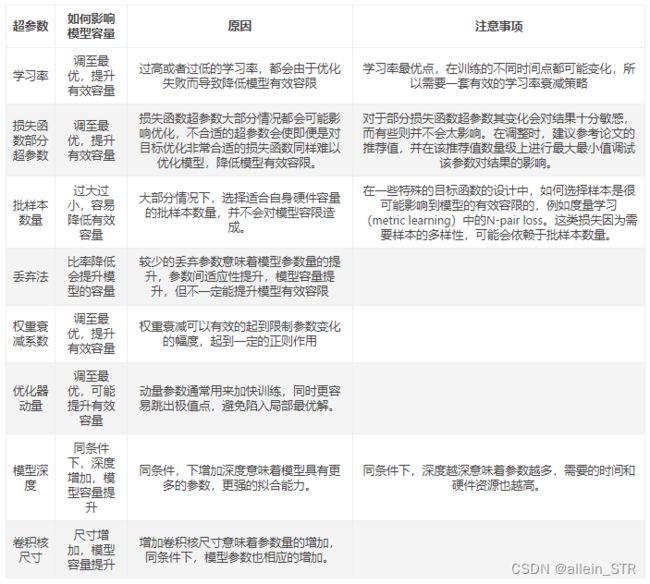
超参具体如何影响模型性能

超参合适的范围

（2）网格搜索

网格搜索类似于手动调优，对所有超参值进行排列组合，然后创建模型，并评估和选择最佳模型。

考虑上面的例子，它有两个超参数 k_value =[2,3,4,5,6,7,8,9,10] 和 algorithm = [‘auto’ , ’ball_tree’ , ’kd_tree’ , ’brute’]，在这种情况下，它总共构建了9 * 4 = 36个不同的模型。

缺点：

排列组合交叉验证，导致速度很慢。

python代码： 

from sklearn.model_selection import GridSearchCV

knn = KNeighborsClassifier()
grid_param = { 'n_neighbors' : list(range(2,11)) , 
              'algorithm' : ['auto','ball_tree','kd_tree','brute'] }
              
grid = GridSearchCV(knn,grid_param,cv = 5)
grid.fit(X_train,y_train)

#best parameter combination
grid.best_params_

#Score achieved with best parameter combination
grid.best_score_

#all combinations of hyperparameters
grid.cv_results_['params']

#average scores of cross-validation
grid.cv_results_['mean_test_score']

（3）随机搜索

为什么考虑随机搜索？--在许多情况下，所有的超参数可能并非同等重要。

随机搜索从超参数空间中随机选择参数组合，参数按 n_iter 给定的迭代次数进行选择。随机搜索已经被实践证明比网格搜索得到的结果更好。

缺点： 

不能保证给出最佳的参数组合。

python代码：

from sklearn.model_selection import RandomizedSearchCV

knn = KNeighborsClassifier()

grid_param = { 'n_neighbors' : list(range(2,11)) , 
              'algorithm' : ['auto','ball_tree','kd_tree','brute'] }

rand_ser = RandomizedSearchCV(knn,grid_param,n_iter=10)
rand_ser.fit(X_train,y_train)

#best parameter combination
rand_ser.best_params_

#score achieved with best parameter combination
rand_ser.best_score_

#all combinations of hyperparameters
rand_ser.cv_results_['params']

#average scores of cross-validation
rand_ser.cv_results_['mean_test_score']

（4）贝叶斯搜索

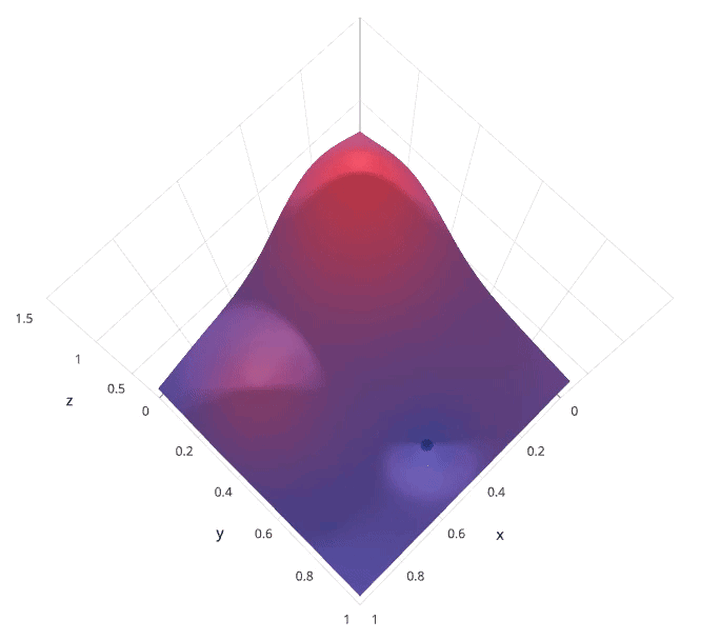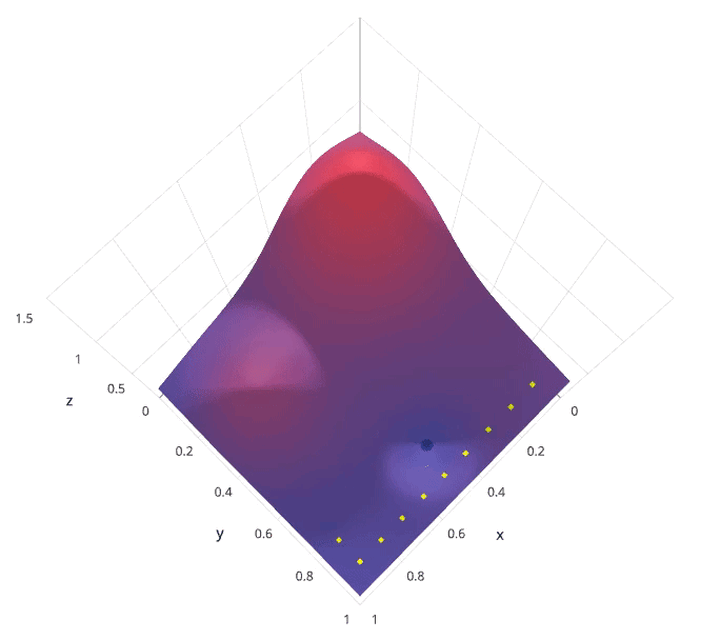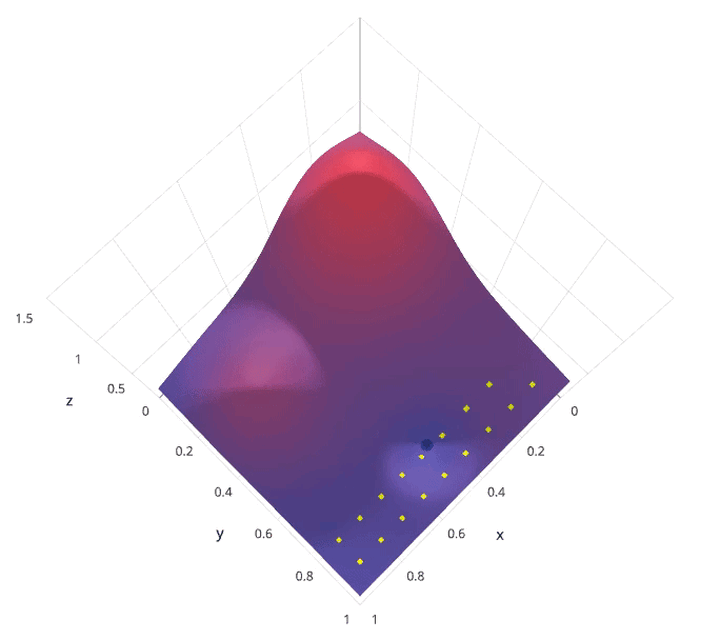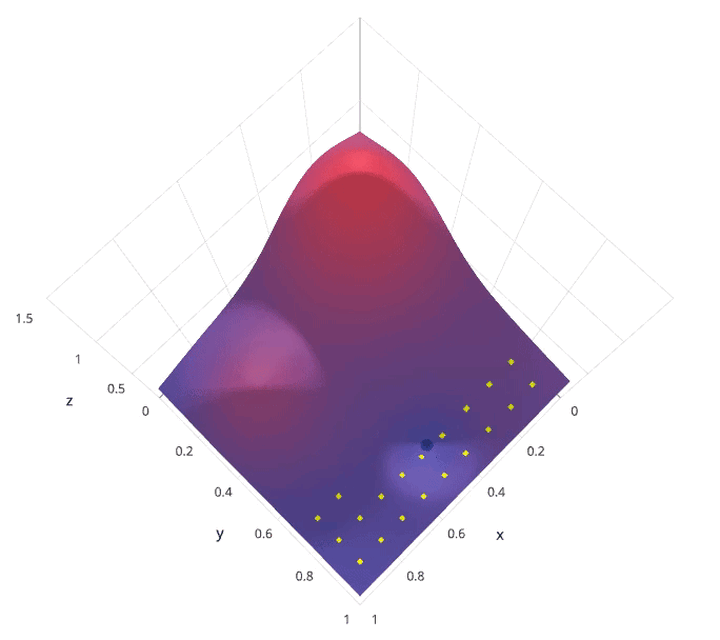
贝叶斯优化属于一类被称为sequential model-based optimization(SMBO)的优化算法。这些算法使用先前对损失 f 的观测，来确定下一个(最佳)点来取样 f。该算法大致可以概括如下。

1. 使用先前计算过的点 X1: n，计算损失 f 的后验期望值。
2. 在一个新的点 Xnew取样损失 f ，它最大化了 f 的期望的某些效用函数。该函数指定 f 域的哪些区域是最适合采样的。

重复这些步骤，直到达到某种收敛准则。

 缺点：

在2维或3维搜索空间中，需要十几个样本才能得到一个良好的替代曲面（surrogate surface）; 增加搜索空间的维数需要更多的样本。

python代码：

from skopt import BayesSearchCV

import warnings
warnings.filterwarnings("ignore")

# parameter ranges are specified by one of below
from skopt.space import Real, Categorical, Integer

knn = KNeighborsClassifier()
#defining hyper-parameter grid
grid_param = { 'n_neighbors' : list(range(2,11)) , 
              'algorithm' : ['auto','ball_tree','kd_tree','brute'] }

#initializing Bayesian Search
Bayes = BayesSearchCV(knn , grid_param , n_iter=30 , random_state=14)
Bayes.fit(X_train,y_train)

#best parameter combination
Bayes.best_params_

#score achieved with best parameter combination
Bayes.best_score_

#all combinations of hyperparameters
Bayes.cv_results_['params']

#average scores of cross-validation
Bayes.cv_results_['mean_test_score']

3. 新型超参优化方法--VeLO

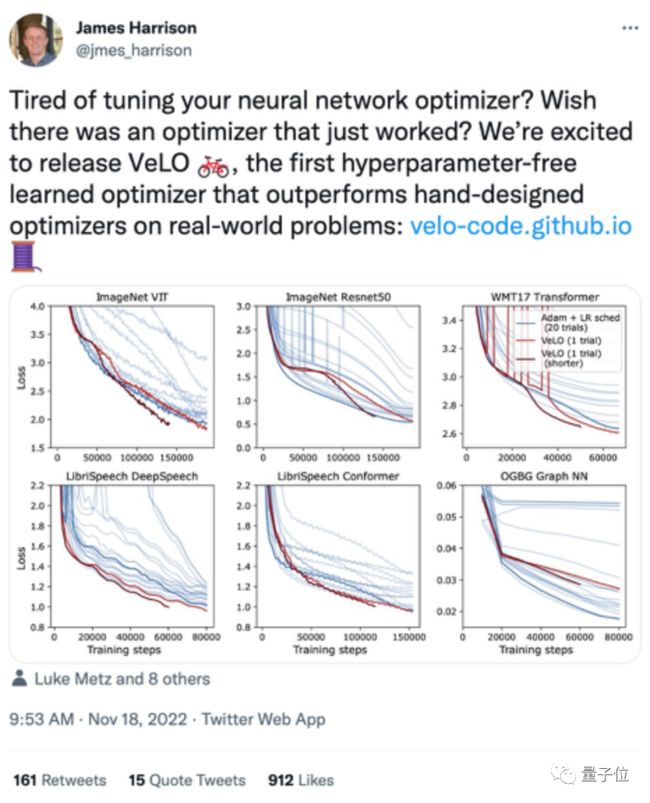
让AI自己调整超参数，谷歌大脑新优化器火了，自适应不同任务，83个任务训练加速比经典Adam更快。

现在，谷歌大脑搞出了一个新的优化器VeLO，无需手动调整任何超参数，直接用就完事了

与其他人工设计的如Adam、AdaGrad等算法不同，VeLO完全基于AI构造，能够很好地适应各种不同的任务。

当然，效果也更好。论文作者之一Lucas Beyer将VeLO与其他“重度”调参的优化器进行了对比，性能不相上下。所以，这个基于AI的优化器是如何打造的？

如何打造AI优化器？        

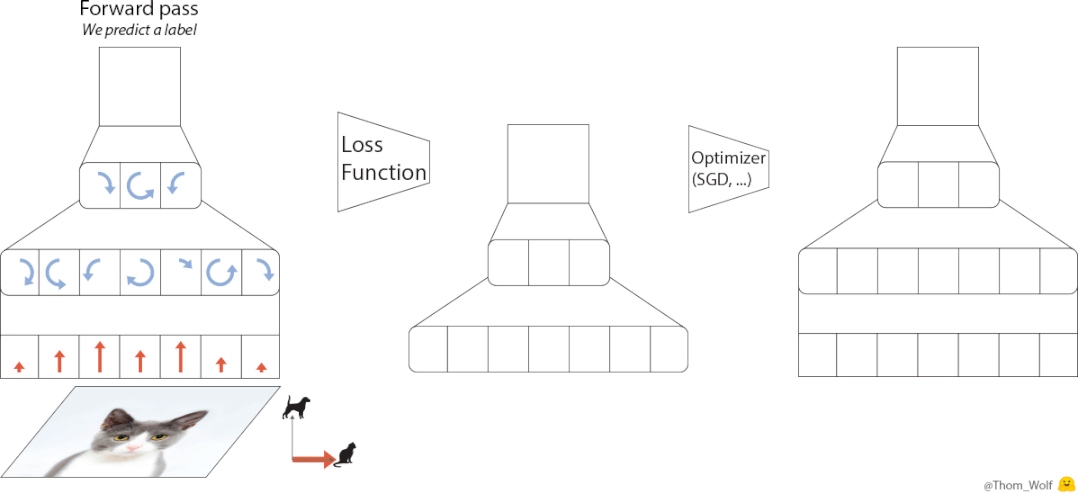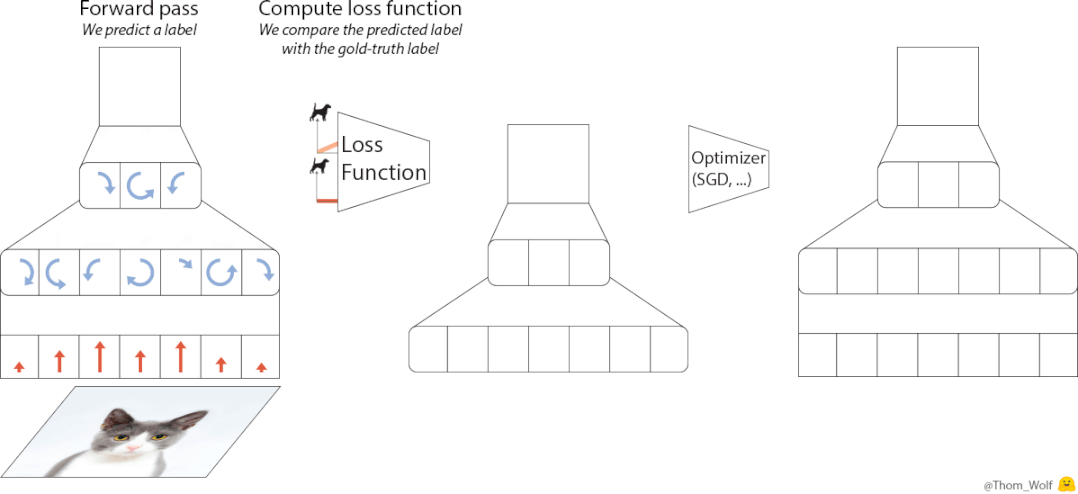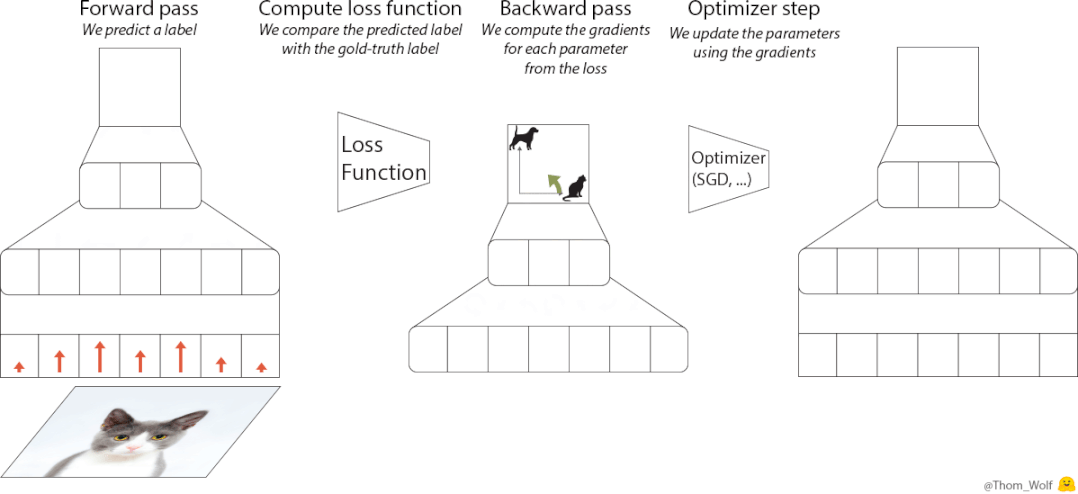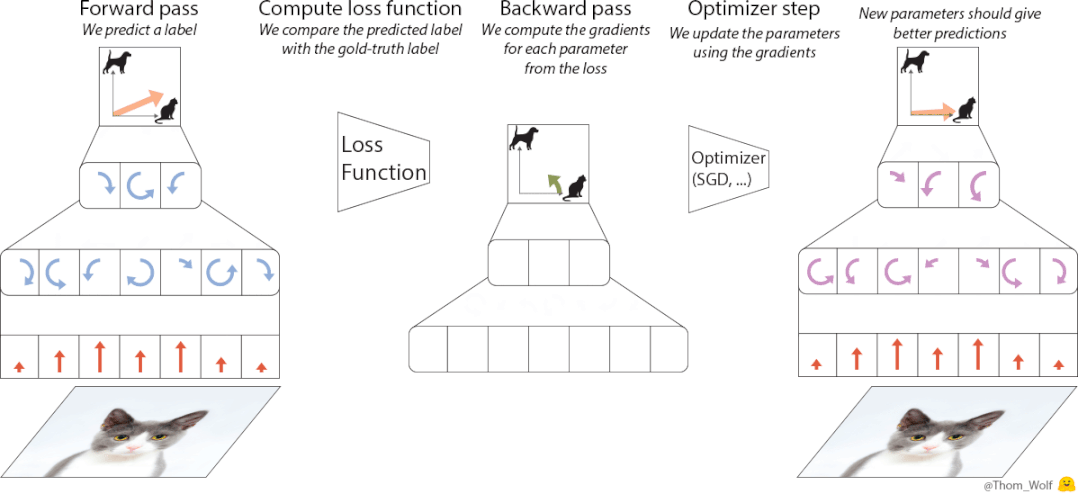
在训练神经网络的过程中，优化器（optimizer）是必不可少的一部分。

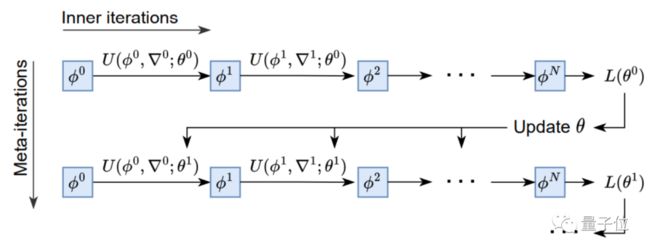
设计上，优化器的原理基于元学习的思路，即从相关任务上学习经验，来帮助学习目标任务。

相比迁移学习，元学习更强调获取元知识，它是一类任务上的通用知识，可以被泛化到更多任务上去。

基于这一思想，VeLO也会吸收梯度并自动输出参数更新，无需任何超参数调优，并自适应需要优化的各种任务。

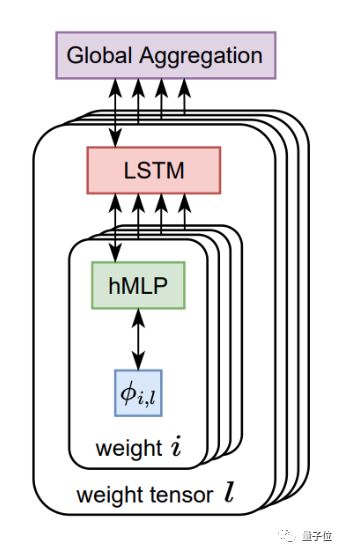
架构上，AI优化器整体由LSTM（长短期记忆网络）和超网络MLP（多层感知机）构成。

其中每个LSTM负责设置多个MLP的参数，各个LSTM之间则通过全局上下文信息进行相互协作。

训练上，AI优化器采用元训练的方式，以参数值和梯度作为输入，输出需要更新的参数。

经过4000个TPU月（一块TPU运行4000个月的计算量）的训练，集各种优化任务之所长后，VeLO终于横空出世。

新型优化器评价

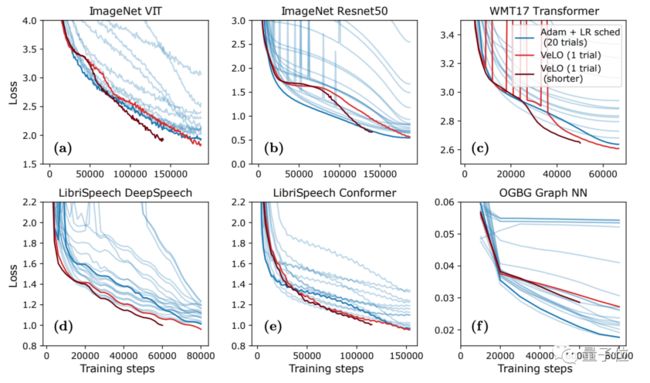
结果表明，VeLO在83个任务上的加速效果超过了一系列当前已有的优化器。

其中y轴是相比Adam加速的倍率，x轴是任务的比例。

结果显示，VeLO不仅比无需调整超参数的优化器效果更好，甚至比仔细调整过超参数的一些优化器效果还好：

与“经典老大哥”Adam相比，VeLO在所有任务上训练加速都更快，其中50%以上的任务比调整学习率的Adam快4倍以上，14%以上的任务中，VeLO学习率甚至快上16倍。

而在6类学习任务（数据集+对应模型）的优化效果上，VeLO在其中5类任务上表现效果都与Adam相当甚至更好：

 值得一提的是，这次VeLO也被部署在JAX中，看来谷歌是真的很大力推广这个新框架了。

目前VeLO已经开源，感兴趣的小伙伴们可以去试试这个新的AI优化器。

GitHub地址：
https://github.com/google/learned_optimization/tree/main/learned_optimization/research/general_lopt

论文地址：
https://arxiv.org/abs/2211.09760

---

参考资料：

1. https://thuijskens.github.io/2016/12/29/bayesian-optimisation/
2. scikit-optimize Documentation
3. bayesian-optimization Documentation
4. PyVision公众号  Sivasai Yadav Mudugandla
5. https://www.jianshu.com/p/6602c76cc801

6. https://twitter.com/jmes_harrison/status/1593422054971174912

7. https://medium.com/huggingface/from-zero-to-research-an-introduction-to-meta-learning-8e16e677f78a#afeb

8. https://mp.weixin.qq.com/s/QLzdW6CMkcXWQbGjtOBNwg