超分文章记录 SRCNN-FSRCNN-ESPCN-VDCN-DRCN-RDN-LapSRN-SRDenseNet-SRGAN

1.Learning a Deep Convolutional Network for Image Super-Resolution（SRCNN 2014 ECCV ）

1、总结

第一篇用深度学习做超分的文章，就是用深度学习来表示传统方式。结构比较简单。
源码地址：
SRCNN CODE

2、思路

先用 bicubic interpolation把图像scale到目标大小，然后通过提特征，非线性映射，然后恢复成图像。

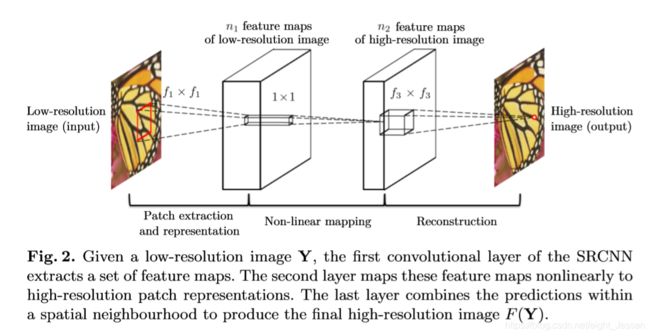
网络结构代码表示：

import tensorflow as tf 
from tensorflow.contrib import slim 
class SRCNN: 
 def __init__(self): 
   pass 
 def model(self, inputs, padding='VALID', name='srcnn'): 
   with tf.variable_scope(name, reuse=tf.AUTO_REUSE): 
   inputs = inputs / 255.0 
   net = slim.conv2d(inputs, 64, [9, 9], padding=padding, scope='conv1_1') 
   net = slim.conv2d(net, 32, [1, 1], padding=padding, scope='conv2_1') 
   net = slim.conv2d(net, 1, [5, 5], padding=padding, activation_fn=None, scope='conv3_1') 
   return net 
 def __call__(self, inputs, padding='VALID', name='srcnn'): 
   return self.model(inputs, padding, name) 

2.Accelerating the super-resolution convolutional neural network（2016 ECCV）

文章主页
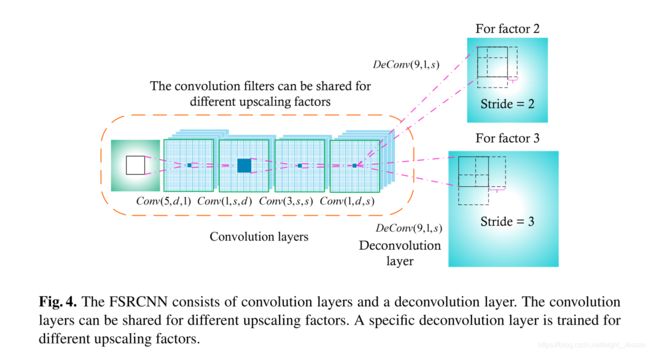
相比SRCNN，FSRCNN

• 网络参数量减少了，效果也没有下降。
• 不需要预处理做图片上采样，只需要做网络最后一层deconv的改动，网络比较好迁移训练和测试。

反卷积传送门

思路

网络分为了
feature exraction—shrinking—mapping—expanding—deconvolution

1.Feature Extraction

第一步是提取特征。这一步由于没有像SRCNN先做上采样，所以$5\ast 5$的滤波器的感受野就相当于SRCNN $9\ast 9$的滤波器感受野。这一层可以表示为$Conv(5,d,1)$

2.Shrinking

这一步降低了计算消耗。用了$1\ast 1$的filter,这一层可以表示为$Conv(1,s,d),s<<d$，对LR的特征实现了降维。

3. Non-linear mapping

这一层最重要的是深度（depth, the number of layers)和宽度（width, the number of filters in a layer)。这一部分可以表示为 $m\cdot Conv(3,s,s)$

4.Expanding

这一层就像是shrinking的逆操作。直接从前面的LR特征做超分结果是不理想的，所以多加了这一层去扩展HR层的维度。这一层是$Conv(1,d,s)$。

5.Deconvolution

$DeConv(9,1,d)$

6.PReLU

Parametric Rectified Linear Unit
ReLU和PReLU可以表示为：
$$f(x_i)=max(x_i,0)+a_{i}min(0,x_i)$$
如果$a_i=0$就是ReLU

7.Overall structure

$Conv(5,d,1)-PReLU-Conv(1,s,d)-PReLU-m\ast Conv(3,s,s)-PReLU-Conv(1,d,s)-PReLU-DeConv(9,1,d)$
三个敏感变量$s,d,m$
$FSRCNN(d,s,m)$
计算复杂度（不计PReLU） $O(25d+sd+9m{s}^2+ds+81d)S_{LR}=O(9m{s}^2+2sd+106d)S_{LR}$

8.Cost function

MSE
$$mi{n}_{\theta }\frac{1}{n}\sum _{i=1}^n||F(Y_s^i;\theta -X_i)|{|}_2^2$$
$Y_s^i$和$X^i$分别是第i个LR和HR图片对,$F(Y_s^i;\theta )$是网络的输出

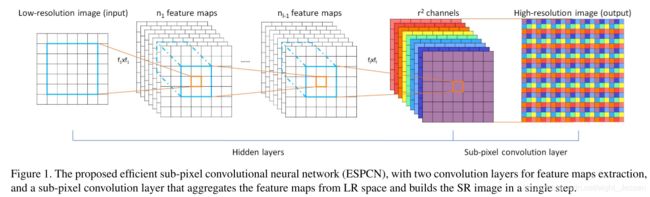
3.Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network（ESPCN CVPR2016）

反卷积传送门
反卷积传送门2

Method

1.数据处理

先对原来的图像做高斯模糊，模拟相机的点扩散，然后做下采样。
先在LR图片上过了$l$层卷积，然后用一个 sub-pixel convolution layer上采样LR feature maps产生$I^{SR}$
比如对于一个L层的网络,$L-1$层可以描述为：
$$f^1(I^{LR};W_1,b_1)=\varphi (W_1\ast I^{LR}+b_1)$$
$$f^l(I^{LR};W_{1:l},b_{1,l})=\varphi (W_l\ast f^{l-1}(I^{LR}+b_l))$$
$W_l,b_l,l\in (1,L-1)$,$W_l$是$2D$卷积层，大小为$n_{l-1}\ast n_l\ast k_l\ast k_l$,$n_l$是$l$层的特征数,$\varphi$激活函数，最后一层$f^L$将LR特征映射到HR图片。

2.Deconvolution layer

使用神经网络unscale的方法之一

3.Efficient sub-pixel convolution layer

$$I^{SR}=f^L(I^{LR})=PS(W_L\ast f^{L-1}(I^{LR})+b_L)$$
$PS$这个操作就是，上一步生成的特征层为$H\ast W\ast C\ast r^2$，把他们重新排列成$rH\ast rW\ast C$,对应于上面的第四第五张图就是这个操作
$$PS(T{)}_{x,y,c}=T_{\lfloor x/r\rfloor ,\lfloor y/r\rfloor ,C\cdot r\cdot mod(y,r)+C\cdot mod(x,r)+c}$$
卷积操作$W_L$大小为$n_{L-1}\ast r^{2}C\ast k_L\ast k_L$，当$K_L=\frac{k_s}{r}$还有$mod(k_s,r)=0$时，相当于在LP空间上的 sub-pixel convolution卷积

这篇文章有关于sub-pixel conv更详细的介绍

4.Loss

pixel-wise mean squared error(MSE)
$$l(W_{1:L},B_{1:L})=\frac{1}{r^{2}HW}\sum _{x=1}^{rH}\sum _{x=1}^{rW}(I_{x,y}^{HR}-f_{x,y}^L(I^{L}R){)}^2$$

4.Accurate Image Super-Resolution Using Very Deep Convolutional Networks（VDSR CVPR2016)

4.1、总结

这篇文章提出了一个very deep网络结构，通过在深层网络结构中多次级联小滤波器，有效利用大图像区域上的上下文信息。还有通过之学习残差加快训练。
作者提出了SRCNN的几个缺点：

• 只依赖与图像小区域的上下文信息
• 训练收敛太慢
• 网络只能实现 single scale
  作者的创新点在：
• 利用大图像区域的上下文信息
• 只依靠残差学习，同时用大的学习率，梯度裁剪实现
• 解决single network multe-scale SR problem

4.2 Method

4.2.1 网络结构

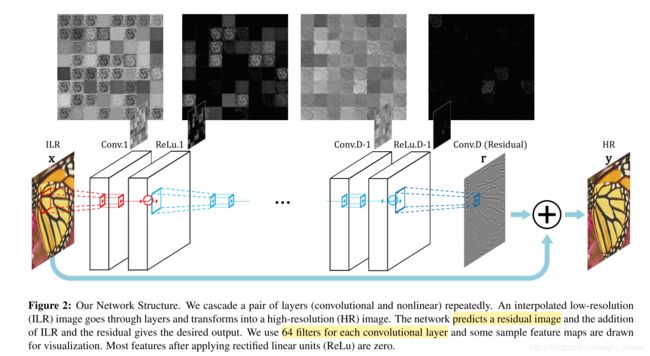
使用了d层，除了第一层和最后一层，都用了$3\ast 3\ast 6$的滤波器，第一层作用于输入图片，最后一层输出图片。做了pad zeros处理。

4.2.2 训练

输入图像$x$，输出$y$，训练集$\{x^{(i)},y^{(i)}{\}}_{i=1}^N$
$\hat{y}=f(x)$,$\hat{y}$ estimate
训练目标，最小化MSE $\frac{1}{2}||y-f(x)|{|}^2$
Residual-Learning
在SRCNN中，输入的信息从输入传到了输出，由于有许多权重层，这就变成了一种端到端的关系，需要非常长的内存。对于这个原因，消失/爆炸梯度问题是至关重要的。通过residual-learning解决这个问题。
残差图片可以表示为 $r=y-x$，很多为0或者很小，loss function就是$\frac{1}{2}||r-f(x)|{|}^2$,$f(x)$是网络的预测结果。
网络的loss层有三个输入：residual estimate, network input (ILR image) and ground truth HR image。 Loss是重建图像和gt的欧氏距离。
High Learning Rates
使用比较高的学习率，同时用一个可调的梯度裁剪最大限度地提高速度，同时抑制爆炸梯度。
Adjustable Gradient Clipping，裁剪到$[-\theta ,\theta ]$。为了最大化收敛，梯度裁剪范围为$[-\frac{\theta }{\gamma },\frac{\theta }{\gamma }]$,$\gamma$是当前的学习率。
Multi-Scale
训练集有多种scale的图像

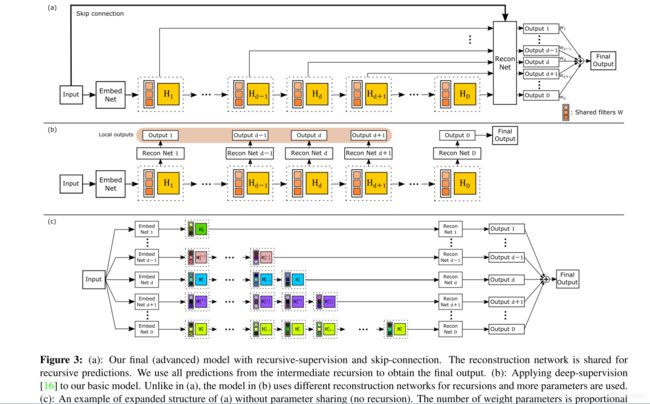
5.Deeply-Recursive Convolutional Network for Image Super-Resolution（DRCN CVPR 2016 Oral）

5.1 总结

网络越深，就能更大的感受野，但是网络越大，于是作者提出了deeply-recurisive convolution network（DRCN)，不需要引入太多的网络参数。但是DRCN会比较男训练，于是通过recursive-supervision和skip-connection来解决。

• recursive-supervision 每一次递归出来的特征都会重建出HR图像，计算结果
• skip-connection from input to the reconstruction layer. LR图像和HR图像包含的信息是相同的，但是LR图像在网络的前向传播过程中，信息会丢失，所以加上skip-connection.
  
  

5.2 Method

网络的输入是插值图像

5.2.1 Basic Model

就是上面的两张图，网络分成了三个部分：embedding, inference and reconstruction

• embedding net 将输入图像表示成特征
• inference net 主要解决SR部分，不断地recursive,感受野变大
• reconstruction 将最后的特征转换到图片空间

每个子网络只有一层，每一层就像是MLP，使用$3\ast 3$的卷积核。对于embedding net, 使用$3\ast 3$卷积核是因为对于超分辨率，图像梯度的信息比强度更丰富。对于其他的两个网络，就是考虑了邻近的像素信息。

数学公式

网络的输入是插值后的图片$x$,预测目标图片$y$,网路输出是$\hat{y}=f(x)$，分别用$f_1$,$f_2$,$f_3$表示三个子网络，那么$f(x)=f_3(f_2(f_1(x)))$。
对于embedding,$f_1$
假设$f_1(x)$的输出是矩阵$H_0$,把隐藏层记成$H_{-1}$，有
$$H_{-1}=max(0,W_{-1}\ast x+b_{-1})$$
$$H_0=max(0，W_0\ast H_{-1}+b_0)$$
$$f_1(x)=H_0$$
对于inference,$f_2$
输入为$H_0$,输出为$H_D$。用相同的权重和偏差$W$,$b$做所有的操作。
$H_d=g(H_{d-1})=max(0,W\ast H_{d-1}+b)$
$g$是单一 一层的操作，$d=1,...,D$
$$f_2=(g\ast g\ast ...\ast )g(H)=g^D(H)$$
$\ast$表示一个函数组合，$g^d$表示 g的$d-fold$积。
对于重建网络reconstructin, $f_3$
$$H_{D+1}=max(0,W_{D+1}\ast H_D+b_{D+1})$$
$$\hat{y}=max(0,W_{D+2}\ast H_{D+1}+b_{D+2})$$
$$f_3(H)=\hat{y}$$

模型属性

梯度会出现问题

5.2 Advanced Model

Recuisive-Supervision

监督每一次的结果消除梯度爆炸或者消失的问题，inferece网络出来的每一次结果，reconstruction网络都会重建，最终有$D$个结果。用所有的$D$计算最终的结果。测试中求平均。
训练过程中监测信号直接从loss传到早期递归
思考：反向传播，梯度是怎么回传的

Skip-Connection

直接将输入引入到reconstruction层。这样reconstruction就有两个信息来源

Mathematical Formulation

$${\hat{y}}_d=f_3(x,g^{(d)}(f_1(x)))$$
$d=1,2,...,D$
输出可以堪称是输入和特征$H_d$的叠加，$f_3(x,H_d)=x+f_3(H_d)$
最后的输出是所有中间预测的权值平均 $$\hat{y}=\sum _{d=1}^D{w}_d\cdot {\hat{y}}_d$$
$w_d$是递归期间从每个中间隐藏状态重建的预测的权重。
$w_d$是怎么得到的

5.3 训练

目标函数

训练集$\{x^{(i)},y^{(i)}{\}}_{i=1}^N$，目标准确预测$\hat{y}=f(x)$
对于中间输出，有loss： $l_1(\theta )={\sum }_{d=1}^D{\sum }_{i=1}^N\frac{1}{2DN}||y^{(i)}-{\hat{y}}_d^{(i)}|{|}^2$
对于最后的输出，有loss: $l_2(\theta )={\sum }_{i=1}^N\frac{1}{2N}||y^{(}i)-{\sum }_{d=1}^D{w}_d\cdot {\hat{y}}_d^{(i)}|{|}^2$
总的loss: $L(\theta )=\alpha l_1(\theta )+(1-\alpha )l_2(\theta )+\beta ||\theta |{|}^2$
$\alpha$前期比较大有利于训练收敛，后面逐渐变小。

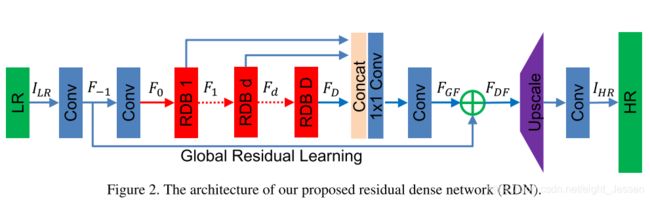
6.Residual Dense Network for Image Super-Resolution(RDN 2018CVPR)

用上分层的信息做图像的超分重建,代码地址

• 提出了一个RDN(residual dense network），网络用上了LR图片的多层特征，并且有多种退化的模型
• 提出了RDB（residual dense block）模块，用了CM（contiguous memory）机制，用了LFF(local feature fusion)
• 用了global feature fusion

6.1 Method

6.1.1 网络结构

网络输入记为$I_{LR}$和$I_{SR}$，整体结构包括了四部分：

• shallow featre extraction net(SFENet)
• residual dense blocks (RDBs)
• dense feature fusion (DFF)
• up-sampling net (UPNet)

$$I_{SR}=H_{RDN}(I_{LR})$$
第一层提取了LR输入的特征$F_{-1}$，$F_{-1}=H_{SFE1}(I_{LR})$,$F_0=H_{SFE2}(F_{-1})$
假设有$D$个RSB, 第$d$个输出$F_d$ ，
$F_d=H_{RDB,d}(F_{d-1})=H_{RDB,d}(H_{RDB,d-1}(...(H_{RDB,1}(F_0))...))$
$H_{RDB,d}$是一个函数的组合操作，比如卷积和修正线性函数
然后进行DFF(dense feature fusion) ，包括了GFF(global feature fusion)和GRL(global residual learning)$F_{DF}=H_{DFF}(F_{-1},F_0,F_1,...,F_D)$
然后上采样,用了ESPCN。

6.1.2 Residual Dense Block

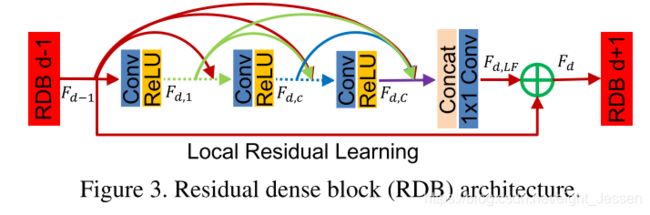
RDB 包括了dense connected layers, local feature fusion(LFF), local residual learning, 学了了一个contiguous memory(CM)机制。
CM
第d个RDB的输入，输出分别记为$F_{d-1}$,$F_d$,各自都有$G_0$个feature maps,有
$F_{d,c}=\sigma (W_{d,c}[F_{d-1},F_d,...,F_{d,c-1}])$
$\sigma$是ReLU函数，假设$F_{d,c}$有G个feature maps，$[F_{d-1},F_d,...,F_{d,c-1}]$表示里面第$(d-1)$个RDB的特征和第$d$个RDB的第$1,...,(c-1)$卷积特征的结合，最终有$G_0+(C-1)\ast G$个特征。
LFF
$F_{d,LF}=H_{LFF}^d([F_{d-1},F_{d,1},...,F_{d,c},...,F_{d,C}])$
$H_{LFF}^d$是第$d$个RDB的$1\ast 1$卷积。
LRL Local residal learning
为了提高信息流。
$F_d=F_{d-1}+F_{d,LF}$

6.1.3 Dense Feature Fusion

DFF包含了global feature fusion(GFF)和global residual learning
GFF
$F_{GF}=H_{GFF}([F_1,...,F_D])$
$[F_1,...,F_D]$是每个RDB的特征，$H_{GFF}$包括了$1\ast 1$和$3\ast 3$的卷积。$1\ast 1$用于自适应地融合具有不同级别的一系列功能。
Global residual learning
$F_{DF}=F_{-1}+F_{GF}$
$F_{-1}$是浅层特征，其他的是全局融合特征。

6.2 评价指标

用PSNR和SSIM对变换后的YCbCr空间的Y通道（即亮度）进行结果评估

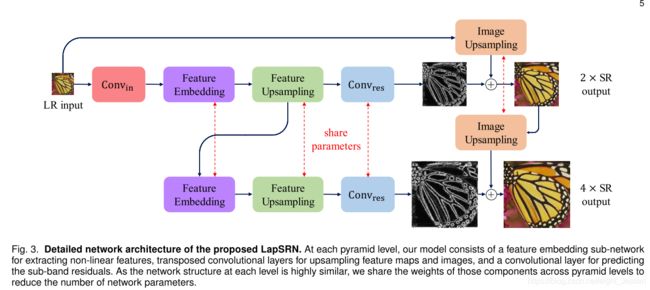
7.Fast and Accurate Image Super-Resolution with Deep Laplacian Pyramid Networks（LapSRN TPAMI 2018)

论文工作页面

7.1 网络结构

基于拉普拉斯金字塔框架，有$lo{g}_2^S$层金字塔结构，S为缩放的系数。比如如果为8倍($S=8$)，那么就有三层结构。

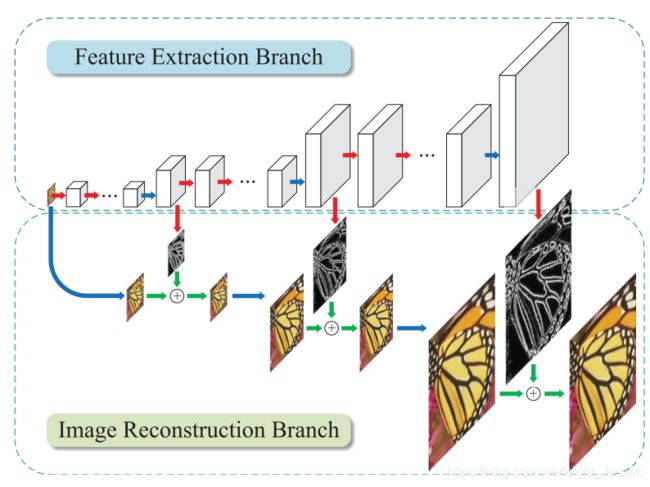
7.1.1 特征提取分支

包括了三部分：

• a feature embedding sub-network（高纬度非线性特征映射）
• a tranposed convolution layer（上采样提取的特征）
• a convolutional layer（预测sub-band残差图像）
  第一个金字塔结构还有一个额外的特征提取网络从LR图像提取特征，之后的金字塔结构直接把上一层upscaled之后的特征作为输入

7.1.2 图片重建网络

图片通过一个转置卷积层（transposed convolutional layer）上采样2倍，这个卷积层初始是$4\ast 4$的双线性核。然后组合上采样的图和预测的残差图片产生HR图像。然后用于下一层的输入。每一层是相同的结构。

7.2 Feature embedding sub-network

网络越深，参数越多，下面用两种方法减少参数

7.2.1 金字塔层间参数共享

因为每层金字塔都是相同的任务，放大相同的倍数
最终网络参数与放大倍数无关，使用一个参数集就可以实现放大不同的倍数。

7.2.2 金字塔层内参数共享

将feature embedding sub-network扩展成深度递归层
如果每个feature embedding sub-network有$R$次循环模块，模块有$D$层，那么整个网络的深度为$$depth=(D\ast R+1)\ast L+2$$
$L=lo{g}_{2}S$，括号里的1表示转置卷积层，$2$表示作用与输入图片的卷积和最后一层预测残差的卷积。

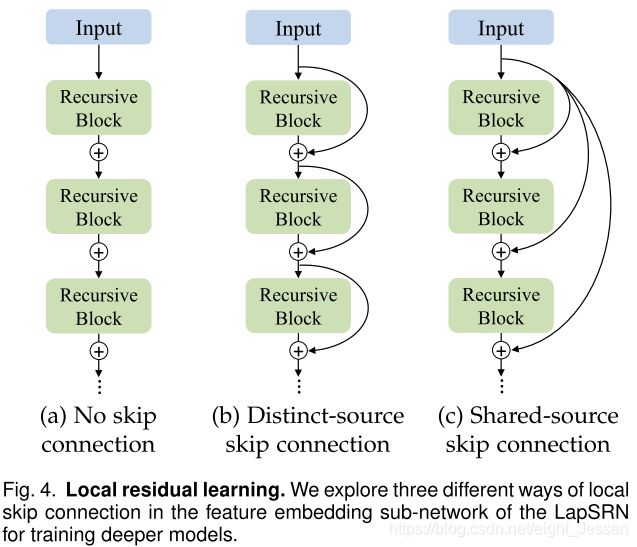
7.2.3 Local residual learning

解决梯度爆炸\消失问题，在feature embedding sub-network探索了三种方法：

• No sikp connection，表示为$LapSR{N}_{NS}$
• Distinct-source skip connection，记为$LapSR{N}_{DS}$
• Shared-source skip connection，记为$LapSR{N}_{SS}$

7.3 Loss function

输入$x$,网络参数$\theta$,输出$\hat{y}$，网络可表示为$\hat{y}=f(x;\theta )$，尽可能与gt $y$相同。将第$l$层的残差图像表示为${\hat{r}}_l$，upscale的图像记为$x_l$和对应的${\hat{y}}_l$，第$l$层输出的图像为${\hat{y}}_l{x}_l+{\hat{r}}_l$，使用双三次插值算法将gt下采样到$y_l$大小。鲁棒损失函数来处理异常值
$$L_S(y,\hat{y};\theta )=\frac{1}{N}\sum _{i=1}^N\sum _{l=1}^L\rho (y_l^{(i)}-{\hat{y}}_l^{(i)})=\frac{1}{N}\sum _{i=1}^N\sum _{l=1}^L\rho ((y_l^{(i)}-x_l^{(i)})-{\hat{r}}_l^{(i)})$$
$\rho (x)=\sqrt{(x^2+{ϵ}^2)}$，Charbonnier penalty function L1范数的一个可微变量，通常设$ϵ$为$1e-3$。
在提出的模型中，每个level，$s$都有他loss方程和对应的gt,这种multi-scale的监督使网络重建图像实现了coarse-to-fine的模式，减少空间混叠伪影。

7.4 Multi-scale training

使用了不同的scale去训练网络,同时不同的unsampling scale samples由不同的层输出。最终组合的loss为：
$L(y,\hat{y};\theta )={\sum }_{S\in \{2,4,8\}}{L}_s(y,\hat{y};\theta )$
但是对于基于pre-upsampling的方法，图片可以缩放在任意的scale，但是对于LapSRN，只能是$2^n\ast SR$,$n$为整数。

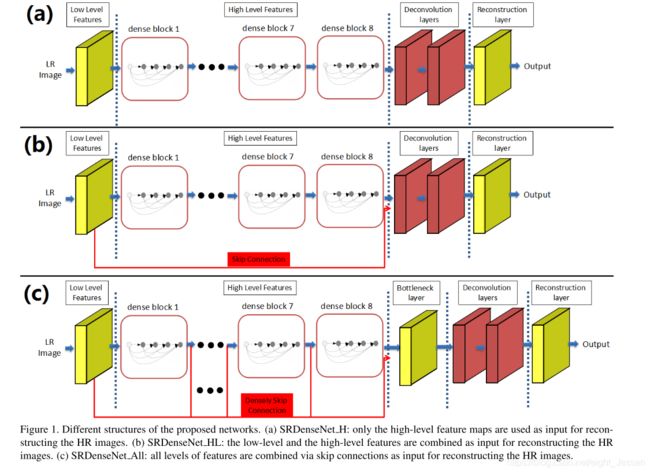
8. Image Super-Resolution Using Dense Skip Connections(SRDenseNet ICCV2017)

使用DenseNet作为网络的基础模块，通过dense skip connections实现SISR

8.1 Method

网络可以分解为几个部分：

• 一个用于学习low-level特征的卷积
• DenseNet模块，用于提取高层信息
• deconvolution反卷积层，用于上采样
  每个卷积后面都加上ReLU做非线性映射，除了重建层，第i层卷积的输入表示为$X_{i-1}$，输出可表示为$X_i=max(0,w_i\ast X_{i-1}+b_i)$

对于给定的训练图片$\{I_L^k,I_H^k\}$，最小化MSE
$$l(\Theta )=\frac{1}{N}\sum _{k=1}^N||F(I_K^m,\Theta )-I_H^k|{|}_2^2$$

8.2 DenseNet blocaks

第i层活接受之前所有层的特征作为输入
$$X_i=max(0,w_i\ast [X_1,X_2,...,X_{i-1}]+b_i)$$
$[X_1,X_2,...,X_{i-1}]$表示concatenation,如果对于每一个block,有8个卷积层，每层有$k$个特征输出，那么每个Dense Block输出的特征是$k\ast 8$,这里$k$就是指增长率，表示每层能为最终重建层提供多少信息。

8.3 Deconvolution layers

两个$3\ast 3$的反卷积核，feature map为256

8.4 Combination of feature maps

见上图

8.5 Bottleneck and Reconstruction layers

如果所有的block出来的特征信息送入到反卷积网络，会增加计算消耗和增大模型。所以需要先较小输入的特征信息。故用了$1\ast 1$的卷积核作为bottleneck。最终送入到deconvolution层的特征层为256.然后使用$3\ast 3$的网络做反卷积。

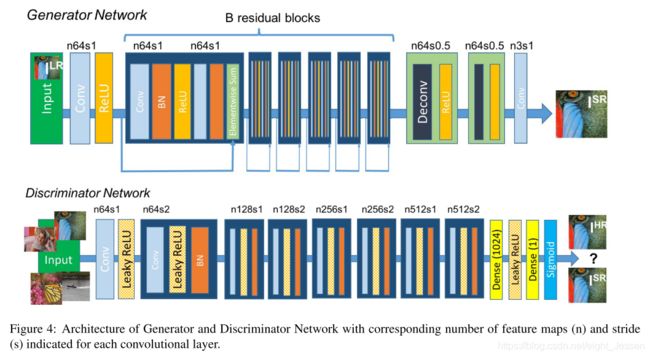
9.Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network

图片超分是一个一对多的问题
之前的方法对超分比例比较大的图片无法恢复出精细的纹理细节。之前只要用MSE PSNR
作者用GAN的方法，得到更精细的图片细节，引入了一个perceptual loss function，包括了对抗loss和内容loss两部分。

9.1 Method

$I^{LR}$由$I^{HR}$经过高斯滤波然后下采样倍数$r$得到。如果低像素图片$I^{LR}$是$W\ast H\ast C$，上采样结果是$rW\ast rH\ast C$。我们的最终目标是训练一个生成函数G来估计给定的LR输入图像对应的HR对应图像。
于是训练一个generator ,CNN $G_{{\theta }_G}$，${\theta }_G=\{W_{1:L};b_{1:L}\}$表示L层网络的权重和方差，通过$l^{SR}$ 优化，对于$I_n^{HR},n=1,...,N$对应的$I_n^{LR},n=1,...,N$
$${\hat{\theta }}_G=argmi{n}_{{\theta }_G}\frac{1}{N}\sum _{n=1}^N{l}^{SR}(G_{{\theta }_G}(I_n^{LR}),I_n^{HR})$$
作者设计了一个perceptual loss $l^{SR}$ 最为几个loss的组合。对恢复后的SR图像进行了清晰的特征建模。

9.1.1 Adversarial Network Architecture

$$\begin{array}{r}mi{n}_{{\theta }_G}ma{x}_{{\theta }_D}{E}_{I^{HR}\sim p_{train}(I^{HR})}[log{D}_{{\theta }_D}(I^{HR})]+\\ E_{I^{LR}\sim p_G(I^{LR})}[log(1-D_{{\theta }_D}(G_{{\theta }_G}(I^{LR})))]\end{array}$$

9.1.2 Perceptual Loss

给了权重参数${\gamma }_i,i=1,...,K$。定义 $l^{SR}={\sum }_{i=1}^K{\gamma }_i{l}_i^{SR}$ 作为单个损失函数的加权和。

• Content Loss
  pixel-wise MSE loss可以由下面计算$$l_{MSE}^{SR}=\frac{1}{r^{2}WH}\sum _{x=1}^{rW}\sum _{y=1}^{rH}(I_{x,y}^{HR}-G_{{\theta }_G}(I^{LR}{)}_{x,y}{)}^2$$作者设计了VGG loss,${\varphi }_{i,j}$表示由第i个最大池化层后第j个卷积层出来的特征。定义为一个欧拉距离。
  $$I_{VGG/i,j}^{SR}=\frac{1}{W_{i,j}{H}_{i,j}}\sum _{x=1}^{W_{i,j}}\sum _{j=1}^{H_{i,j}}({\varphi }_{i,j}(I^{HR}){)}_{x,y}-{\varphi }_{i,j}(G_{{\theta }_G}(I^{LR}{)}_{x,y}{)}^2$$
• Adversarial Loss
  generative loss,基于所有数据在discriminator $D_{{\theta }_D}(G_{{\theta }_G}(I^{LR}))$上的概率分布
  $$l_{Gen}^{SR}=\sum _{n=1}^N-log{D}_{{\theta }_D}(G_{{\theta }_G}(I^{LR}))$$
• Regularization Loss
• 基于总体的方差
  $$l_{TV}^{SR}=\frac{1}{r^{2}WH}\sum _{x=1}^{rW}\sum _{y=1}^{rH}||\nabla G_{{\theta }_G}(I^{LR}{)}_{x,y}||$$