【Carsim Simulink自动驾驶仿真】基于MPC的速度控制

本人也是刚开始探索，大家一起讨论一起进步！
项目介绍：
教程为北理工的无人驾驶车辆模型预测控制第2版，代码为开源代码。所用的仿真软件为Carsim2020.0和MatlabR2021a。使用MPC控制思想对车辆进行速度控制，并给出仿真结果。
效果如下：

Carsim的基本配置

Carsim一共可以分为三大部分：

• 前处理：涉及对车型的选择和对工况的设置
• 计算：可以使用Carism直接计算，也可以外接其他计算软件，比如Matlab。
• 后处理：将运行的结果表现成动画和图像。
  具体分布如下：
  

车型的选择

车型选择E-Class SUV，最好开一个新的Dataset。

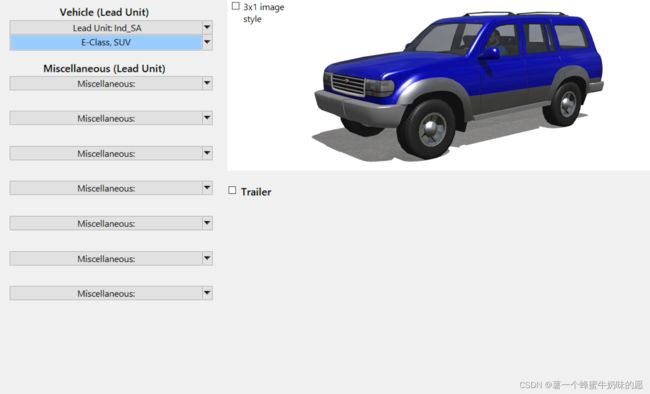
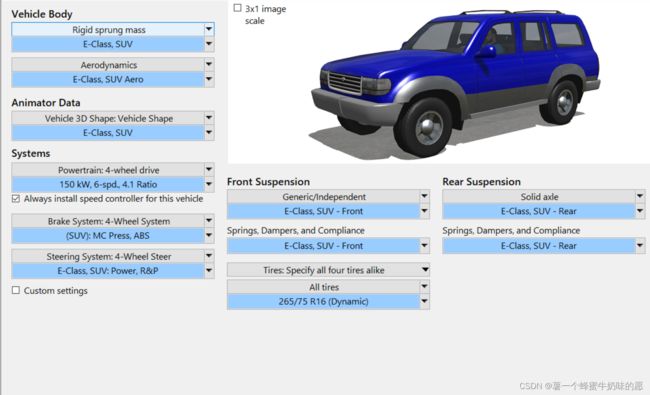
工况设置

新开一个Dataset。因为我们需要在MATLAB中控制汽车，不需要模型自身施加驱动力和制动力所以驱动控制和制动控制设置为无。挡位选择自动升档。本项目无横向控制，所以转向盘选择”Driver path follower“控制。道路设置长一点，仿真设置120s，具体参数设置如下：

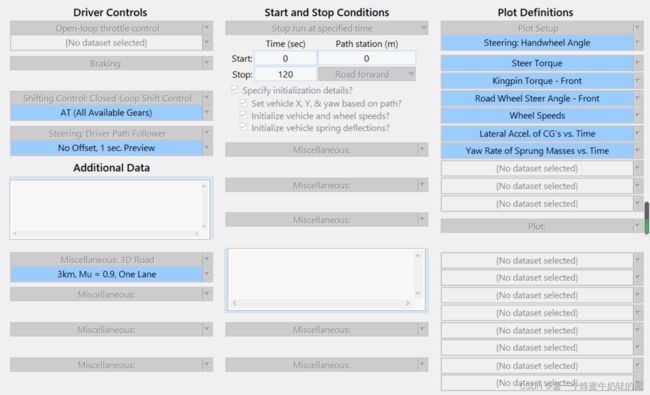
Carsim与Matlab的接口设置

在设置完前处理之后，准备使用MATLAB中的Simulink对其进行控制和计算。在计算那一栏的Model中选择Model:Simulink。之后建立一个新的Dataset。具体设置如下：

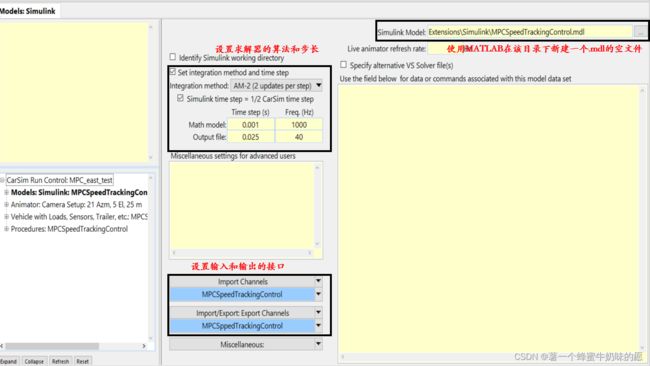
这里的输入设置为IMP_THROTTLE_ENGINE（油门输入）、IMP_PCON_BK制动主缸压力[MPa]。

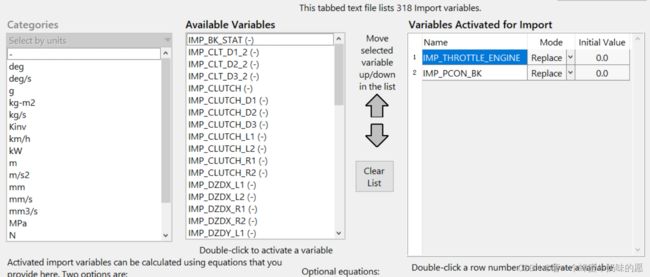
输出设置为车速和加速度：

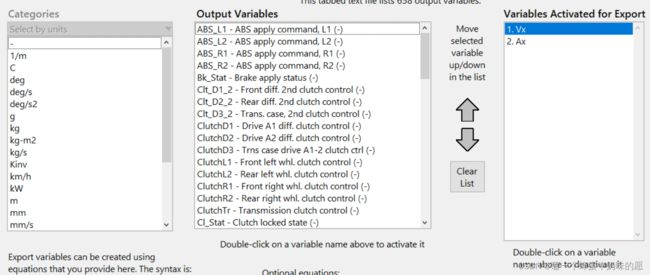
设置好之后点击：Send to Simulink

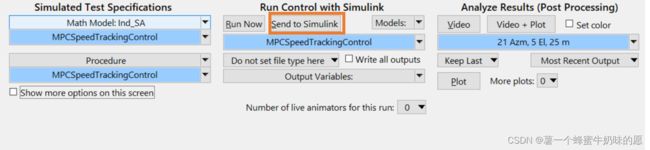
Matlab 框架搭建

在使用Carsim发送过去数据之后，点击MATLAB中的Simulink，此时的Library Browser中应该会出现Carsim S-Function：

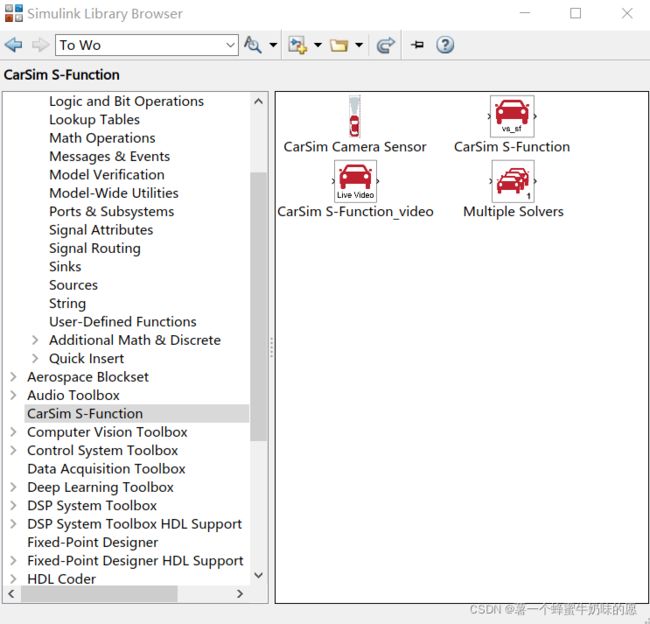
将Carsim S-Functioin拖入Simulink模块，同时在User-Defined Functions中找到S-Function并拖入Simulink模块。构建如下图所示的框架：

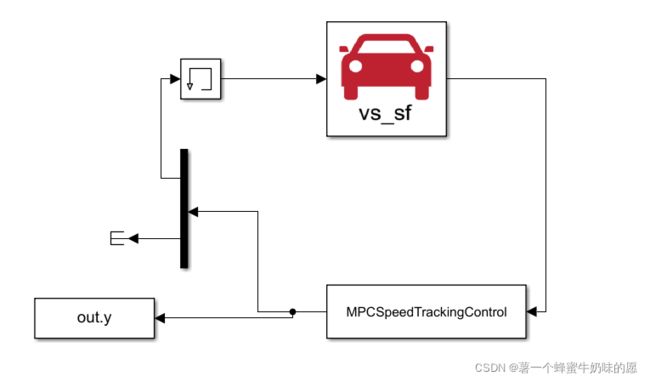
这里稍微解释一下这个框架：
我们希望使用MPC对汽车的速度进行控制。对于MPC，我们的输入是自己设定的期望速度，汽车当前的速度和加速度，这些量暂且统一称为决策变量，根据这些变量，MPC计算之后会给出相应的控制，让汽车去调整到我们期望的速度，这里的控制是油门和制动主缸压力，这样就构成了一个反馈。因为在使用MPC的时候，我们还希望看一些其他量的变化，所以在MPC模块的输出不仅仅是两个控制量，还会有其他的量，使用Terminator模块将不需要输入进Carsim模块终止掉。使用To Workspace模块将MPC所有输出模块导入到MATLAB里面，方便画图。

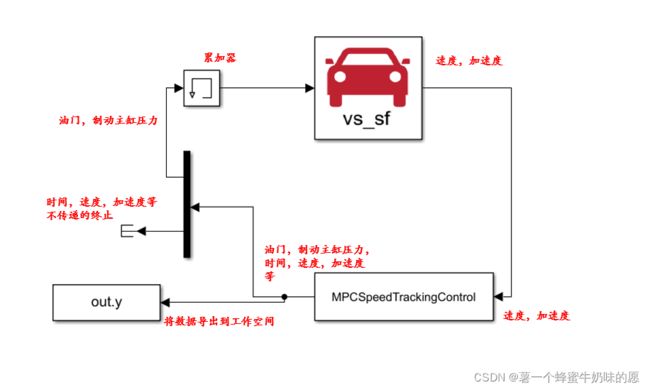
如果不需要看其他参数，可以直接构建如下框架：

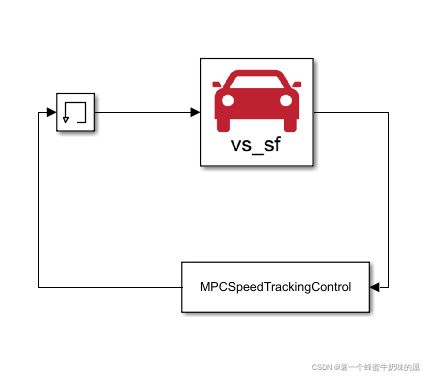
MPC速度控制理论

问题描述

汽车的速度控制可以参考下图(来自北理工的书)：其可以分为上位控制器和下位控制器。

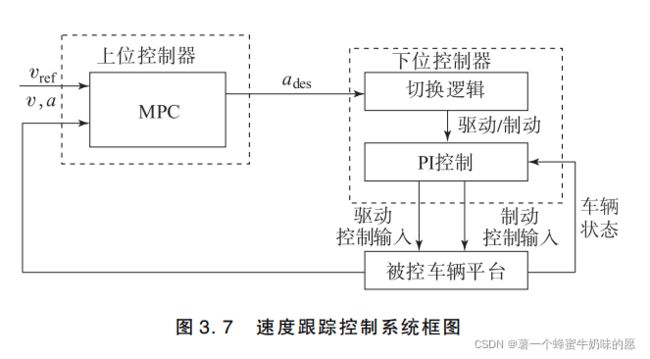
在机器人控制中可以分为底层控制-感知-决策。感知方面其实我们默认是做好的，而且本例也不涉及。这个上位控制可以理解为决策，根据车辆的当前速度加速度状态和期望的速度，判断该如何进行加速度的选择。下位控制器可以理解为底层控制，当车辆做出决策给出应当进行的控制的时候，需要准确的进行这个控制实现。

速度跟踪MPC建模

车辆的纵向控制可以使用一阶惯性系统来表示：
$$\dot{a}=\frac{K}{{\tau }_d}(a_{des}-a)$$
其中$K=1$为系统的增益；${\tau }_d$为时间常数。将上式和速度加速度关系写成矩阵形式，变成状态方程：
$$\dot{x}=Ax+Bu$$
展开表示为：
$$\left(\begin{array}{c}\dot{v}\\ \dot{a}\end{array}\right)=\left(\begin{array}{cc}0& 1\\ 0& \frac{-1}{{\tau }_d}\end{array}\right)\left(\begin{array}{c}v\\ a\end{array}\right)+\left(\begin{array}{c}0\\ \frac{K}{{\tau }_d}\end{array}\right)a_{des}$$
使用前向欧拉法，进行离散：
$$x(k+1)=A_{k}x(k)+B_{k}u(k)$$
展开表示为：
$$\left(\begin{array}{c}v(k+1)\\ a(k+1)\end{array}\right)=\left(\begin{array}{cc}1& T_s\\ 0& 1-\frac{T_s}{{\tau }_d}\end{array}\right)\left(\begin{array}{c}v(k)\\ a(k)\end{array}\right)+\left(\begin{array}{c}0\\ \frac{K{T}_s}{{\tau }_d}\end{array}\right)a_{des}(k)$$
速度$v$作为系统的输出，输出方程可以表示为：
$$y(k)=Cx(k),C=[10]$$
以上就是模型预测控制中的模型建立。

系统的控制目标定义为：速度跟踪精度，同时还要避免过大的加速度和冲击。
$$J=\sum _{i=1}^{N_p}(y_p(k+i|k)-y_{ref}(k+i|k){)}^2+\sum _{i=1}^{N_c}(\Delta u(k+i){)}^2$$
系统的约束为加速度及其变化率；
$$\begin{gathered} u_{min}\le u(k+i)\le u_{max},i=0,1,...,N_e-1 \\ \Delta u_{min}\le \Delta u(k+i)\le \Delta u_{max},i=0,1,...,N_c-1 \end{gathered}$$
这样我们就把MPC的模型建立完毕了，基本框架为：
$$\begin{gathered} minJ \\ s.t.x(k+1)=A_{k}x(k)+B_{k}u(k) \\ {u}_{min}\le u(k+i)\le u_{max},i=0,1,...,N_e-1 \\ \Delta u_{min}\le \Delta u(k+i)\le \Delta u_{max},i=0,1,...,N_c-1 \end{gathered}$$

MPC求解转化为二次型规划求解(把模型约束放入目标函数)

这部分理论性比较强，MPC理论推导参考如何理解MPC模型预测控制理论，这里主要说一下思路和编程所用的公式。

使用模型，对未来的状态和控制进行预测，并给出解析结果

首先为了推导方便，我们进行如下定义：
$$\xi (k|t)=[x(k),u(k-1){]}^T$$
这样我们的离散模型可以写成：
$$\begin{gathered} \xi (k+1)=\widetilde{A_k}\xi (k)+\widetilde{B_k}\Delta u(k) \\ \eta (k)=\widetilde{C_k}\xi (k) \end{gathered}$$
其中这里面的$\widetilde{A_k}=\left(\begin{array}{cc}{A}_k& B_k\\ 0_{m\times n}& I_m\end{array}\right),\widetilde{B_k}=\left(\begin{array}{c}{B}_k\\ I_m\end{array}\right),\widetilde{C_k}=(C_k\mathrm{０})$。这里$m=1,n=2$

证明的具体过程就不在这里赘述，主要思路是，我们希望通过当前的状态来给出控制，那么观察离散模型，可以发现，通过当前的状态，根据离散模型，其实是能给出下一时刻的状态的，甚至是输入，而当得到下一时刻状态的时候又可以根据离散的方程进行预测，得到下下时刻的状态，如此迭代，可以得到预测时域内所有时刻的状态和输入，换句话说这些都可以用初始状态和输入来表示。我们将这些统一写成矩阵形式：
$$Y=\Phi \xi (k)+\Theta \Delta U$$
具体形式为：

将预测的表达式带入目标函数，对其进行改写

我们目前拿到了预测的速度和输入，将其带入到目标函数中，经过改写可以变成：

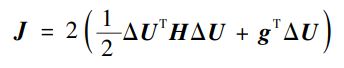
其中：

其实相当于把模型约束放进目标函数中！！！

统一控制变量

现在还剩的约束时控制量和控制增量的约束。而控制量和控制增量存在如下关系：
$$u(k+i)=u(k+i-1)+\Delta u(k)$$
这样可以将最后两个约束写成：

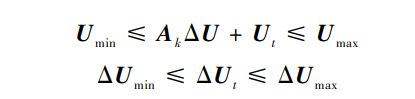
这里：

$A_k$为：

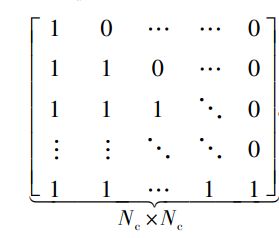
写成二次型问题

通过上述三个步骤，就可以把MPC问题变成一个二次型求解问题：

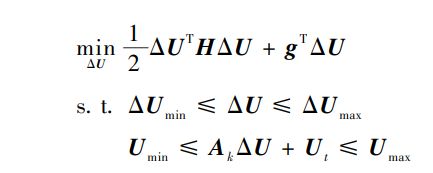
总结一下具体思路：一句话就是把模型放进目标函数中。分步骤说就是首先用建立的模型，当前状态写出预测内的状态和控制。之后将其带入目标函数，并进行整理。最后将剩下的两个约束写成一个统一的形式。这样构建出来的问题使用MATLAB自带的二次规划求解器就可以求解。

注：上述公式也是代码里面的核心公式，如果代码看不懂，可以从这里面寻找答案。

后处理

我们希望跟踪的速度为：

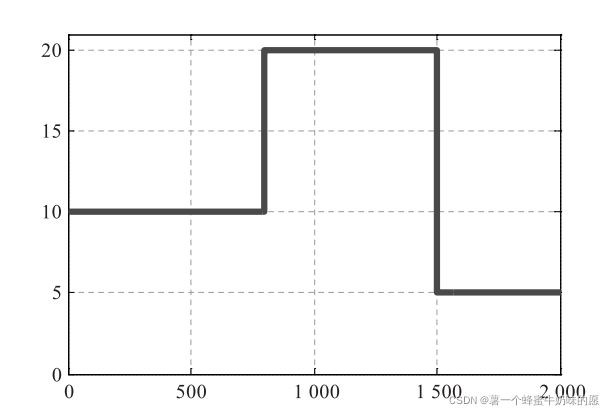
后处理有两种方式：
一种是使用MATLAB：
在命令行窗口输入plot((1:2400),out.y.signals.values(:,4))或者plot(out.y.time,out.y.signals.values(:,4))(因为采样频率是0.05秒一次，一共运行120s)。

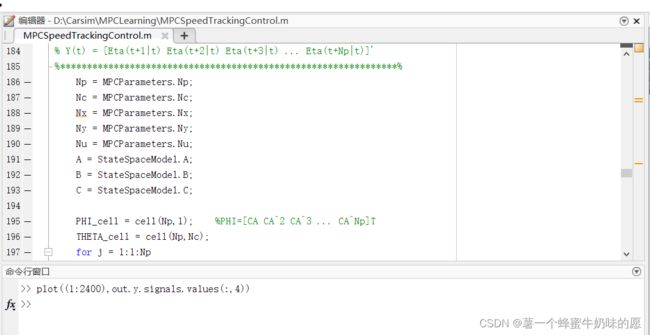
做出图像为：

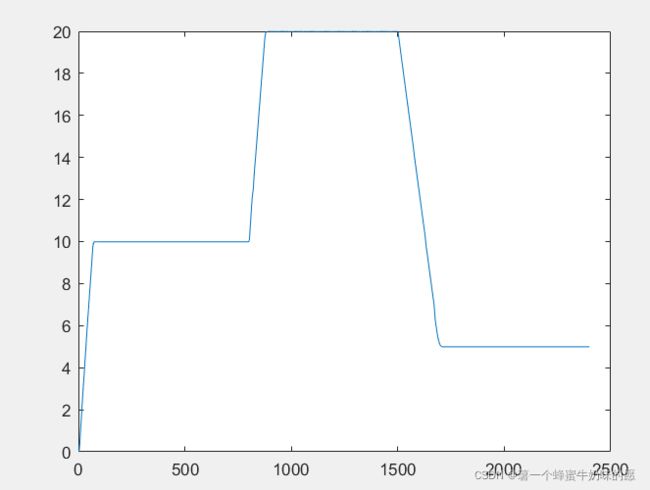
还可以使用Carsim的后处理模块，这里主要是速度跟踪，所以需要Longitudinal speed和time的关系图像。

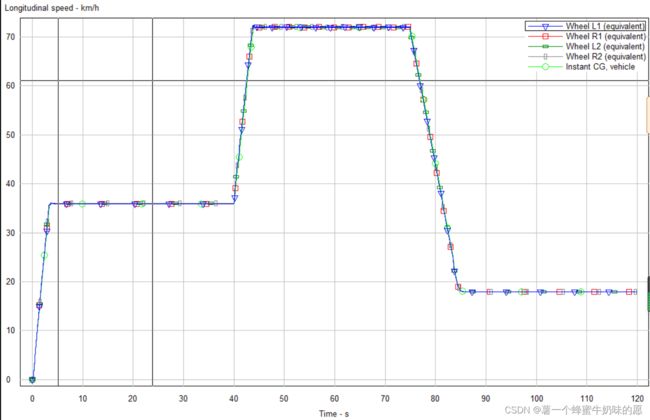
同时Carsim中还提供了仿真的汽车跟踪动画。（如本文开头展示的动画）

附录：Matlab全代码

function [sys,x0,str,ts] =MPCSpeedTrackingControl(t,x,u,flag)
%***************************************************************% 
% Input:
% t是采样时间, x是状态变量, u是输入(是做成simulink模块的输入,即CarSim的输出),
% flag是仿真过程中的状态标志(以它来判断当前是初始化还是运行等)
% Output:
% sys输出根据flag的不同而不同(下面将结合flag来讲sys的含义), 
% x0是状态变量的初始值, 
% str是保留参数,设置为空
% ts是一个1×2的向量, ts(1)是采样周期, ts(2)是偏移量
%---------------------------------------------------------------%
%***************************************************************% 
    switch flag
        case 0 %初始化%
            [sys,x0,str,ts]= mdlInitializeSizes;
        case 2 %更新%
            sys = mdlUpdates(t,x,u);%更新离散变量
        case 3 %输出%
            sys = mdlOutputs(t,x,u);%计算输出
        case {1,4,9} %不用的flag
            sys = [];
        otherwise % 其他flag情况 %
            error(['unhandled flag = ',num2str(flag)]); % Error handling
    end
%  End sfuntmpl

%====================================================================
%初始化，flag=0 
%====================================================================
function [sys,x0,str,ts]= mdlInitializeSizes
    sizes = simsizes;%用于设置模块参数的结构体用simsizes来生成
    sizes.NumContStates = 0; %模块连续状态变量的个数
    sizes.NumDiscStates = 2; %模块离散状态变量的个数,实际上没有用到这个数值，只是用这个来表示离散模块
    sizes.NumOutputs    = 6; %输出量的个数，包括控制量和其他检测量
    sizes.NumInputs     = 2; %输入量的个数，对应Carsim输出量
    
    sizes.DirFeedthrough= 1; %没太懂，好像是时变就需要设为1
    
    sizes.NumSampleTimes= 1; %采样时间的个数
    sys = simsizes(sizes);
    x0 = zeros(sizes.NumDiscStates,1); %初始化状态变量
    str = [];
    ts = [0.05 0];  %采样时间：[period,offset]
    
    %设置一些全局变量
    global InitialGapflag;
        InitialGapflag = 0; 
    global MPCParameters; 
        MPCParameters.Np    =30; %预测时域
        MPCParameters.Nc    =30; %控制时域
        MPCParameters.Nx    =2;  %状态变量
        MPCParameters.Nu    =1;  %控制输入
        MPCParameters.Ny    =1;  %输出变量
        MPCParameters.Ts    =0.05; %设置采样时间
        MPCParameters.Q     =100;  %权重
        MPCParameters.R     =1;   %权重
        MPCParameters.S     =1;   %权重
        MPCParameters.qp_solver = 0; %0: default, quadprog; 1:qpOASES; 2:CVXGEN
        MPCParameters.refspeedT = 0; %0: default, step speed profile; 
                                     %1:sine-wave speed profile
        MPCParameters.umin      = -5.0;  % 最大减速
        MPCParameters.umax      = 3.5;  % 最大加速
        MPCParameters.dumin     = -5.0; % minimum limits of jerk
        MPCParameters.dumax     = 5.0; % maximum limits of jerk
    global WarmStart;
        WarmStart = zeros(MPCParameters.Np,1);
        
%结束
%=============================================================================
%更新离散状态量子函数
function sys=mdlUpdates(t,x,u)
    sys = x;
%结束
%=============================================================================
%计算输出子函数，是速度跟踪控制的主体。
function sys=mdlOutputs(t,x,u)
    global InitialGapflag;
    global MPCParameters;
    global WarmStart;
    a_des = 0; %初始化最优加速度控制量
    a_x = 0; %初始化加速度状态量
    Vx = 0; %初始化车速
    t_Start = tic; %开始计时
    if InitialGapflag < 2 %去掉前两次输入
        InitialGapflag = InitialGapflag + 1;
    else
        InitialGapflag = InitialGapflag + 1;
        
        %------------------Step(1).更新车辆纵向状态--------------------%
        Vx = u(1)/3.6; %单位换算km/h->m/s
        a_x = u(2)*9.8; %单位换算g's->m/s^2
        kesi = [Vx;a_x]; %更新车辆状态向量    
        
        %-------------------Step(2).设定期望速度-----------------------%
        switch MPCParameters.refspeedT
            %------------------设定阶跃式目标车速--------------------------%
            case 0
                SpeedProfile = func_ConstantSpeed(InitialGapflag,MPCParameters);
            %------------------设定sine式目标车速--------------------------%
            otherwise % Unexpected flags %
                error(['unexpected speed-profile:',num2str(MPCParameters.refspeedT)]); % Error handling
        end %  end of switch 
        
        %-------------------Step(3).调用MPC优化求解函数得到最优控制量-----------------------%
        Ts = MPCParameters.Ts;
        StateSpaceModel.A = [1  Ts;
                             0   1];
        StateSpaceModel.B = [0; 1];
        StateSpaceModel.C = [1,0];
        
        [PHI, THETA] = func_Update_PHI_THETA(StateSpaceModel, MPCParameters);
        [H, ~, g] = func_Update_H_f(kesi, SpeedProfile, PHI, THETA, MPCParameters);
        
        switch MPCParameters.qp_solver
            case 0 %default qp-solver:quadprog
                [A,b,Aeq,beq,lb,ub] = func_Constraints_du_quadprog(MPCParameters,a_x);
                options = optimset('Display','off', ...
                            'TolFun', 1e-8, ...
                            'MaxIter', 2000, ...
                            'Algorithm', 'active-set', ...
                            'FinDiffType', 'forward', ...
                            'RelLineSrchBnd', [], ...
                            'RelLineSrchBndDuration', 1, ...
                            'TolConSQP', 1e-8); 
                warning off all  % close the warnings during computation
                
                U0 = WarmStart;
                [U, ~, EXITFLAG] = quadprog(H, g, A, b, Aeq, beq, lb, ub, U0, options); %
                WarmStart = shiftHorizon(U);
                if (1 ~= EXITFLAG) %if optimization NOT succeeded.
                    U(1) = 0.0;
                    fprintf('MPC solver not converged!\n');                  
                end
                a_des =  U(1);
                
                otherwise % Unexpected flags %
                    error(['unexpected qp-solver, Sol_method=',num2str(flag)]); % Error handling
        end %  end of switch 

    end % end of if Initialflag < 1 % 
        
        %****Step(6):  由期望的加速度生成Throttle和Brake;********************%
    [Throttle, Brake] = func_AccelerationTrackingController(a_des);
    t_Elapsed = toc( t_Start ); %computation time 
    sys = [Throttle; Brake;t_Elapsed; Vx; a_x; a_des]; 
% end  %End of mdlOutputs

            
%==============================================================
% sub functions
%==============================================================

        
function [Vref] = func_ConstantSpeed(InitialGapflag, MPCParameters)
    %Ts = MPCParameters.Ts; %采样时间=0.05s
    Np = MPCParameters.Np; %预测时域：30
    Vref = cell(Np,1);
    
    % 自定义阶梯的形式
    if InitialGapflag < 400
        Vset = 10;
    else
        if InitialGapflag < 800
            Vset = 10;
        else
            if InitialGapflag < 1500
                Vset = 20;
            else
                Vset = 5;
            end
        end
    end
    
    for i = 1:1:Np
        Vref{i,1} = Vset;
    end
    
    
function [PHI, THETA] = func_Update_PHI_THETA(StateSpaceModel, MPCParameters)
%***************************************************************%
% 预测输出表达式 Y(t)=PHI*kesi(t)+THETA*DU(t) 
% Y(t) = [Eta(t+1|t) Eta(t+2|t) Eta(t+3|t) ... Eta(t+Np|t)]'
%***************************************************************%
    Np = MPCParameters.Np;
    Nc = MPCParameters.Nc;
    Nx = MPCParameters.Nx;
    Ny = MPCParameters.Ny;
    Nu = MPCParameters.Nu;
    A = StateSpaceModel.A;
    B = StateSpaceModel.B;
    C = StateSpaceModel.C;
    
    PHI_cell = cell(Np,1);    %PHI=[CA CA^2 CA^3 ... CA^Np]T
    THETA_cell = cell(Np,Nc); 
    for j = 1:1:Np
        PHI_cell{j,1}=C*A^j;
        for k = 1:1:Nc
            if k<=j
                THETA_cell{j,k}=C*A^(j-k)*B;
            else
                THETA_cell{j,k} = zeros(Ny,Nu);
            end
        end
    end
    PHI=cell2mat(PHI_cell);    % size(PHI)=[(Ny*Np) * Nx]
    THETA=cell2mat(THETA_cell);% size(THETA)=[Ny*Np Nu*Nc]
% end %EoF

function[H, f, g] = func_Update_H_f(kesi, SpeedProfile, PHI, THETA, MPCParameters)
%***************************************************************%
% trajectory planning
%***************************************************************%

     Np = MPCParameters.Np;
     Nc = MPCParameters.Nc;   
     Q  = MPCParameters.Q;
     R  = MPCParameters.R;
     
     Qq = kron(eye(Np),Q);
     Rr = kron(eye(Nc),R);
     
     Vref = cell2mat(SpeedProfile);
     error1 = PHI*kesi;
     
     H = THETA'*Qq*THETA +Rr;
     f = (error1'-Vref')*Qq*THETA;
     g = f';
 % end %EoF

 function  [A, b, Aeq, beq, lb, ub] = func_Constraints_du_quadprog(MPCParameters, um)
 %************************************************************************%
% generate the constraints of the vehicle
%  
%************************************************************************%
    Np = MPCParameters.Np;
    Nc = Np;    
    dumax = MPCParameters.dumax;
    umin = MPCParameters.umin;  
    umax = MPCParameters.umax;  
    Umin = kron(ones(Nc,1),umin);
    Umax = kron(ones(Nc,1),umax);
    Ut   = kron(ones(Nc,1),um);
    
    %----(1) A*x<=b----------%
    A_t=zeros(Nc,Nc);
    for p=1:1:Nc
        for q=1:1:Nc
            if p >= q 
                A_t(p,q)=1;
            else 
                A_t(p,q)=0;
            end
        end 
    end 
    A_cell=cell(2,1);
    A_cell{1,1} = A_t; %
    A_cell{2,1} = -A_t;
    A=cell2mat(A_cell);  %
    
    
    b_cell=cell(2, 1);
    b_cell{1,1} = Umax - Ut; %
    b_cell{2,1} = -Umin + Ut;
    b=cell2mat(b_cell);  % 

%----(2) Aeq*x=beq----------%
    Aeq = [];
    beq = [];

%----(3) lb=<x<=ub----------%
    lb=kron(ones(Nc,1),-dumax);
    ub=kron(ones(Nc,1),dumax);
% end %EoF

function u0 = shiftHorizon(u) %shift control horizon
    u0 = [u(:,2:size(u,2)), u(:,size(u,2))];  %  size(u,2))
    
function [Throttle, Brake] = func_AccelerationTrackingController(ahopt)
% 车辆下位控制器将期望加速度转化为油门控制量和制动主缸压力控制量
    K_brake         = 0.3; %0.3
    K_throttle      = 1; %0.05;
    Brake_Sat       = 15;
    Throttle_Sat    = 1;

    if ahopt < 0 % Brake control
        Brake = -K_brake * ahopt;
        if Brake > Brake_Sat
            Brake = Brake_Sat;
        end
        Throttle = 0;
    else % throttle control 
        Brake       = 0;
        Throttle    = K_throttle  *ahopt;
        if Throttle > Throttle_Sat
            Throttle = Throttle_Sat;
        end
        if Throttle < 0
            Throttle = 0;
        end

    end
% end %EoF