机器学习——logistic回归

Logistic 回归算法，又叫做逻辑回归算法，或者 LR 算法（Logistic Regression）。用于解决分类问题。在机器学习中，Logistic 函数通常用来解决二元分类问题，也就是涉及两个预设类别的问题，而当类别数量超过两个时就需要使用 Softmax 函数来解决。

基础概念

分类问题与回归问题

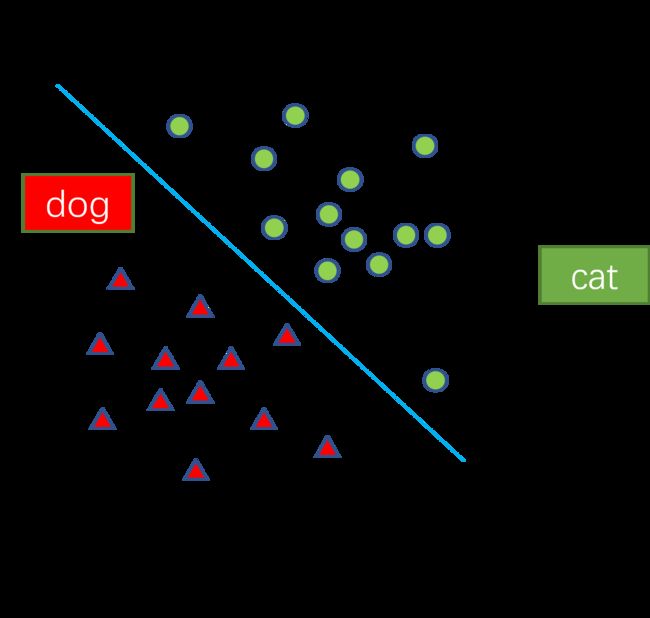
分类问题：预测样本属于哪个或者哪些预定义的类别，其输出值是离散值。如下图，给定一个样本，可以判断其是‘dog’还是‘cat’。

回归问题：用于预测输入变量(自变量)和输出变量(因变量)之间的关系，特别是当输入变量的值发生变化时，输出变量的值也随之发生变化，其输出数据是连续值。如下图，可以根据拟合出来的直线对占地面积的某一个值进行价格的预测。

Sigmoid函数

sigmoid函数，又称为Logistic 曲线，是一个线性函数，由统计学家皮埃尔·弗朗索瓦·韦吕勒发明，其函数表达式如下：
$$y=\frac{1}{1+e^{-z}}$$
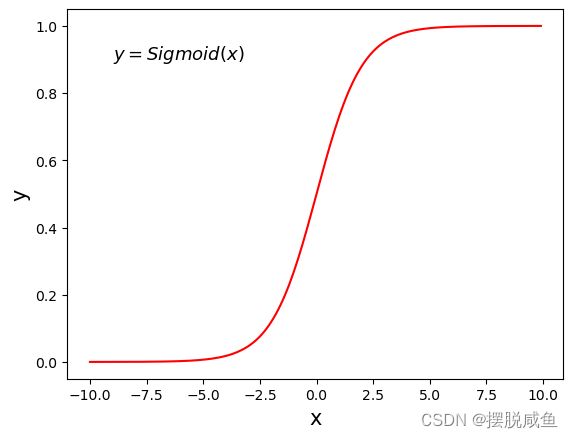
函数图像如下：

从图像上看，对于 Logistic 函数而言，x = 0 是一个有着特殊意义坐标，越靠近 0 和越远离 0 会出现两种截然不同的情况：任何y > 0.5 的数据可以划分到 “1”类中；而y < 0.5 的数据可以划分到 “0”类。因此可以把 Logistic 看做解决二分类问题的分类器。如果想要 Logistic 分类器预测准确，那么 x 的取值距离 0 越远越好，这样结果值才能无限逼近于 0 或者 1。

接下来通过两幅图像来解释为什么需要让x离0越远越好。

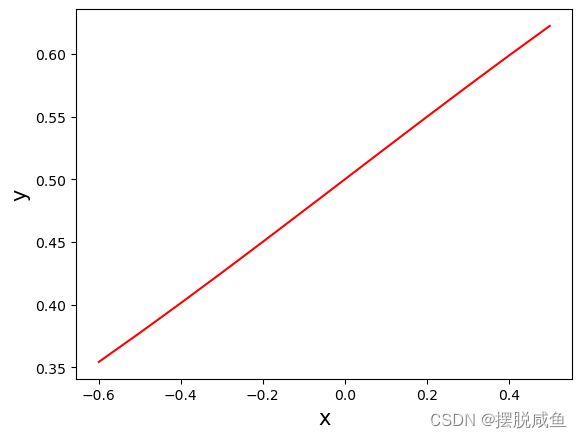
将sigmoid图像x的取值缩小范围至[-0.6 , 0.6]可获得如下的图像：

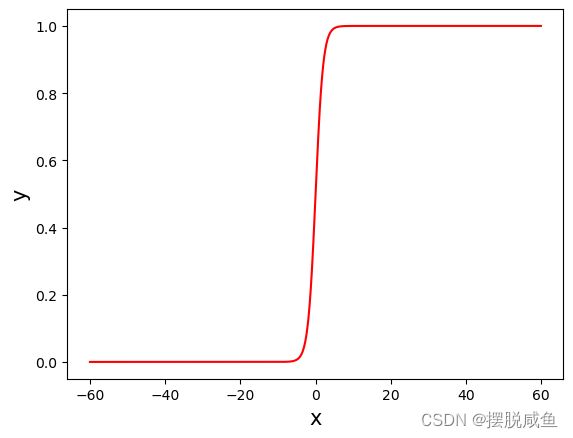
将sigmoid的x取值扩大范围至[-60， 60]可以获得如下图像：

通过对比两幅图像，我们可以发现，当x取值比较小时，sigmoid函数与线性模型无异；当x取值大起来，我们发现sigmoid函数呈现的是一个阶梯式图像，这对我们的二分类来说简直不要太妙。这也就是为什么要采用logistic进行二分类的原因。

基于最优化方法的最佳回归系数确定

问题引出

通过上面的描述，我们发现，为了实现logistic回归分类，我们可以在每一个特征上乘以一个回归系数，然后把相乘的结果累加，代入sigmoid函数中就可以得到一个在[ 0，1 ]范围的值y，我们就可以通过判别y的值来实现分类。（例：y > 0.5为1类，y < 0.5为0类 ）

公式描述：
$$z={\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b$$

z：分类特征与回归系数计算值

w：回归系数矩阵（最佳系数） - ->待求

x：分类的输入数据

b：转置向量（常数） - ->待求

$$y=\frac{1}{1+e^{-z}}$$

带入z可得：
$$y=\frac{1}{1+e^{{\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b}}$$

由上式可以做出以下假设

y：样本x作为正例的可能性

1 - y：样本x作为反例的可能性

y /（1 - y）：几率，反映了x作为正例的相对可能性

由于y的函数有分式和指数e的，所以我们采用对数函数对其进行一种映射：
$${\ln }_{}\frac{y}{1-y}={\ln }_{}\frac{p(y=1|x)}{p(y=0|x)}={\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b$$

$$p(y=1|x)=\frac{{\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b}{1+{\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b}$$

$$p(y=0|x)=\frac{1}{1+{\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b}$$

p(y = 0|x)：表示反例的概率

P(y = 1|x)：表示正例的概率

通过上述的计算结果，我们发现，这变成了求最佳系数w以及转置常数b。

极大似然估计

原理：极大似然估计是建立在极大似然原理的基础上的一个统计方法，是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。通过若干次试验，观察其结果，利用试验结果得到某个参数值能够使样本出现的概率为最大，则称为极大似然估计。即利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。

假设集合样本中各个样本独立分布，考虑一个样本集D，对参数向量θ进行估计。
$$样本集：D=(x_1,x_2...x_n)$$

$$p(D|\theta )称为(x_1,x_2...x_n)的似然函数$$

$$l(\theta )=p(D|\theta )=p(x_1,x_2...x_n|\theta )=\prod _{i=1}^{N}p(x_i|\theta )$$

$$如果\hat{\theta }是参数空间中能是似然函数l(\theta )最大的\theta 值，则\hat{\theta }应该是最可能的参数值，那么\hat{\theta }就是\theta 的极大似然估计值。记为：$$

$$\hat{\theta }=d(x_1,x_2....x_n)=d(D)$$

$$\hat{\theta }(x_1,x_2....x_n)称为极大似然估计值$$

计算步骤如下：

• 确定待求解的未知参数，如均值、方差或特定分布函数的参数等.
• 计算每个样本的概率密度为
• 根据样本的概率密度累乘构造似然函数：
• 通过似然函数最大化（求导为0），求解未知参数θ，为了降低计算难度，可采用对数加法替换概率乘法，通过导数为0/极大值来求解未知参数。
• 最大化样本属于其真实标记的概率，等同于最大化对数似然函数：

$$l(w,b)=\sum _{i=1}^{m}lnp(y_i|x_i;w_i,b)$$

• 转化为最大化逻辑斯蒂似然函数求解

$$\beta =(\mathbf{w};b),\hat{x}=(\mathbf{x},1),则{\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b，可简写成{\beta }^T\hat{x}$$

$$令p_1(\widehat{x_i;\beta })=p(y=1|\widehat{x_i};\beta )$$

$$p_0(\widehat{x_i;\beta })=p(y=0|\widehat{x_i;\beta })=1-p_1(\widehat{x_i;\beta })$$

$$p(y_i|\widehat{x_i;w_i},b)=y_i{p}_1(\widehat{x_i;\beta })+(1-y_i)p_0(\widehat{x_i;\beta })$$

• 根据sigmoid函数，似然函数可重写为：

$$l(\beta )=\sum _{i=1}^m(y_i{\beta }^T\widehat{x_i}-ln(1+e^{{\beta }^T\widehat{x_i}}))$$

梯度上升算法

原理：沿着函数的梯度方向找到函数的最大值。如果梯度记为∇，则函数f(x,y)的梯度由 下式表示：
$$▽f(x,y)=\left(\frac{\phi f(x,y)}{\phi x},\frac{\phi f(x,y)}{\phi y}\right)$$
这个梯度意味着要沿x的方向移动 ，沿y的方向移动 。其中，函数f(x,y) 必须要在待计算的点上有定义并且可微。如下图：

说明：如上图，梯度上升算法到达每个点后都会重新估计移动的方向。从P0开始，计算完该点的梯度，函数就根据梯度移动到下一点P1。在P1点，梯度再次被重新计算，并沿新的梯度方向移动到P2。如此循环迭代，直到满足停止条件。迭代的过程中，梯度算子总是保证我们能选取到最佳的移动方向。

梯度上升算法沿梯度方向移动了一步。可以看到，梯度算子总是指向函数值增长最快的方向。这里所说的是移动方向，而未提到移动量的大小。该量值称为步长，记做α。用向 量来表示的话，梯度上升算法的迭代公式如下：
$$w:=w+\alpha {\nabla }_{w}f(w)$$
上述公式将一直被迭代执行，直至达到某个停止条件为止，比如迭代次数达到某个指定值或算 法达到某个可以允许的误差范围。

梯度下降算法

思想：有一个可导函数f(x) , 先任取点（x0,f(x0))，求f(x)在该点x0的导数f"(x0),在用x0减去导数值f"(x0),计算所得就是新的点x1。然后再用x1减去f"(x1)得x2…以此类推，循环多次，慢慢x值就无限接近极小值点。

梯度下降算法与梯度上升算法大同小异，一个追求的是找梯度的最大值，一个是追求找最小值。

公式：
$$w:=w-\alpha {\nabla }_{w}f(w)$$

代码实现

数据集准备：

这次，我们准备的数据集是通过年龄、身高、体重来判断一个人是否患有赖人症状。具体内容将在文章最后阶段分享网盘，可自行查看。

代码解释：

导入需要的库，这里需要注意from numpy import *与import numpy的区别

from numpy import *
import matplotlib.pyplot as plt

sigmoid函数：

# sigmoid函数
def sigmoid(inX):
    return 1.0 / (1 + exp(-inX))

判断分类结果（> 0.5还是< 0.5）

# 分类函数
def classifyVector(inX, weights):
    prob = sigmoid(sum(inX * weights))   # 计算sigmoid值
    if prob > 0.5:                       # 概率大于0.5，返回分类结果1.0
        return 1.0
    else:                                # 概率小于等于0.5，返回分类结果0.0
        return 0.0

通过梯度上升算法获得最佳拟合系数：

# 梯度上升算法
def gradAscent(dataMatIn, classLabels):                            # dataMatIn数据集、classLabels数据标签
    dataMatrix = mat(dataMatIn)                                    # 转换为NumPy矩阵
    labelMat = mat(classLabels).transpose()                        # 转换为NumPy矩阵，并且矩阵转置
    m, n = shape(dataMatrix)                                       # 获取数据集矩阵的大小，m为行数，n为列数
    alpha = 0.001                                                  # 目标移动的步长
    maxCycles = 500                                                # 迭代次数
    weights = ones((n, 1))                                         # 权重初始化为1
    for k in range(maxCycles):                                     # 重复矩阵运算
        h = sigmoid(dataMatrix * weights)                          # 矩阵相乘，计算sigmoid函数
        error = (labelMat - h)                                     # 计算误差
        weights = weights + alpha * dataMatrix.transpose() * error # 矩阵相乘，更新权重
    return weights

数据准备

def logisticTest1():
    # 读取测试集和训练集,并对数据进行格式化处理
    frTrain = open(r'D:\桌面\logistic\test\Train.txt')      # 读取训练集文件
    frTest = open(r'D:\桌面\logistic\test\test.txt')           # 读取测试集文件
    trainingSet = []                              # 创建数据列表
    trainingLabels = []                           # 创建标签列表
    for line in frTrain.readlines():              # 按行读取
        currLine = line.strip().split('\t')       # 分隔
        lineArr = []
        for i in range(3):
            lineArr.append(float(currLine[i]))
        trainingSet.append(lineArr)
        trainingLabels.append(float(currLine[3]))
 
    # 使用改进的随即上升梯度训练
    trainWeights =  gradAscent(array(trainingSet), trainingLabels)
    errorCount = 0                                # 错误数
    numTestVec = 0.0
    for line in frTest.readlines():               # 遍历每行数据
        numTestVec += 1.0                         # 测试集数量加1
        currLine = line.strip().split('\t')
        lineArr = []
        for i in range(3):
            lineArr.append(float(currLine[i]))
        if int(classifyVector(array(lineArr), trainWeights)) != int(currLine[3]):
            errorCount += 1                        # 预测结果与真值不一致，错误数加1
    errorRate = (float(errorCount) / numTestVec)   # 计算错误率
    print("测试的错误率为: %f" % errorRate)
    return errorRate

计算结果的平均

# 求结果的平均值
def multiTest():
    numTests = 10
    errorSum = 0.0
    for k in range(numTests):
        errorSum += logisticTest1()
    print("在 %d 迭代之后， 平均错误率为: %f" % (numTests, errorSum / float(numTests)))

结果展示：

我们可以发现我的错误率简直离谱，主要问题还是因为我的数据集比较小，并且不真实，具有很大的随机性。

接下来看一下通过sklearn实现鸢尾花数据集的logistics回归分类。

代码如下：

from sklearn.linear_model import LogisticRegression
#导入sklearn 中的自带数据集 鸢尾花数据集
from sklearn.datasets import load_iris
# skleran 提供的分割数据集的方法
from sklearn.model_selection import train_test_split
#载入鸢尾花数据集
iris_dataset=load_iris()
# data 数组的每一行对应一朵花，有四个特征是：花瓣的长度，宽度，花萼的长度、宽度
print("data数组类型: {}".format(type(iris_dataset['data'])))
# 前五朵花的数据
print("前五朵花数据:\n{}".format(iris_dataset['data'][:10]))
#分割数据集训练集，测试集
X_train,X_test,Y_train,Y_test=train_test_split(iris_dataset['data'],iris_dataset['target'],random_state=0)
#训练模型
#设置最大迭代次数为3000
log_reg = LogisticRegression(max_iter=3000)
#传递数据
clm=log_reg.fit(X_train,Y_train)
#分类预测,并打印分类结果
print('分类结果：',clm.predict(X_test))
print('y_test中的结果:',Y_test)
#使用性能评估器
print('模型性能：',clm.score(X_test,Y_test))

运行结果：

我们发现，logistics的精度还算不错，并且在分类问题中有着不错的性能。

总结

​ logistic回归解决的是分类问题，虽然网络上有很多库将logistic封装的很好了，但是我们依旧需要从底层学起，只有这样我们才能更好的去了解深层次的东西。只有从底层实现了才知道logistic的优点有：实现简单，容易理解。但是我们也容易发现其也容易发生欠拟合，并且在确定回归系数时的梯度算法容易导致梯度爆炸，导致欠拟合效果。

代码链接和数据集地址：
链接：https://pan.baidu.com/s/13GEHpHQOTea3mBHxQ2rn4A
提取码：ahsg