矩阵分解——python实现

矩阵分解——python实现

算法实现

具体的算法在java实现的那一篇博客中

由于矩阵分解的算法代码实现比较简单，所以很容易使用python进行实现。具体代码如下

# Coding:utf-8
# @Time:2022/6/20,11:48
# @Auther:zhang
# @file:MartixFactorization.py
# @Software:PyCharm
import random
import math
import time


class Triple:
    '''
    用于存储数据
    '''

    def __init__(self, user, item, rating):
        self.user = user
        self.item = item
        self.rating = rating


class MatrixFactorization:
    '''
    矩阵分解算法实现
    '''

    def __init__(self, datasetFileName, numUser, numItem, numRating, ratingLow, ratingHigh):
        '''
        初始化各项参数，同时读入数据集
        :param datasetFileName:  数据集地址
        :param numUser: 用户数量
        :param numItem: 电影项目数量
        :param numRating: 评分数量
        :param ratingLow: 最低预测评分阈值
        :param ratingHigh: 最高预测评分阈值
        '''
        self.numItem = numItem
        self.numUser = numUser
        self.numRating = numRating
        self.ratingLow = ratingLow
        self.ratingHigh = ratingHigh
        self.dataset = []
        self.userSubspace = []
        self.itemSubspace = []
        self.rank = 0
        self.alpha = 0
        self.Lambda = 0
        # 读入数据集
        self.readData(datasetFileName)

    def readData(self, datasetFileName):
        '''
        从文件中读取数据集
        :param datasetFileName: 数据集地址
        :return: None
        '''
        with open(datasetFileName, 'r') as dataset:
            datalines = dataset.readlines()
        for line in datalines:
            mData = line.strip().split(',')
            data = Triple(int(mData[0]), int(mData[1]), float(mData[2]))
            self.dataset.append(data)

    def setParams(self, rank, alpha, Lambda):
        '''
        设置算法参数
        :param rank:  隐空间维度k
        :param alpha: 梯度下降步长
        :param Lambda:
        :return:
        '''
        self.rank = rank
        self.alpha = alpha
        self.Lambda = Lambda

    def initalizeSubspace(self):
        '''
        初始化子空间，使用随机数填充
        :return: None
        '''
        for i in range(0, self.numUser):
            user = [random.uniform(0.0, 10.0) for j in range(0, self.rank)]
            self.userSubspace.append(user)

        for i in range(0, self.numItem):
            item = [random.uniform(0.0, 10.0) for j in range(0, self.rank)]
            self.itemSubspace.append(item)

    def predict(self, userId, itemId):
        '''
        使用子矩阵对数据集未知评分进行预测
        :param userId: 用户ID
        :param itemId: 电影ID
        :return: 预测评分
        '''
        result = 0.0
        for i in range(0, self.rank):
            result += self.userSubspace[userId][i] * self.itemSubspace[itemId][i]
        return result

    def updateNoRegular(self):
        '''
        根据梯度下降法进行子空间的更新
        :return:
        '''
        for i in range(0, self.numRating):
            tempdata = self.dataset[i]
            tempUser, tempItem, tempRating = tempdata.user, tempdata.item, tempdata.rating
            # 计算误差
            tempError = tempRating - self.predict(tempUser, tempItem)
            # 使用梯度下降更新矩阵
            # 更新用户子矩阵
            for j in range(0, self.rank):
                tempValue = 2 * tempError * self.itemSubspace[tempItem][j]
                self.userSubspace[tempUser][j] += tempValue * self.alpha
            # 更新电影子矩阵
            for j in range(0, self.rank):
                tempValue = 2 * tempError * self.userSubspace[tempUser][j]
                self.itemSubspace[tempItem][j] += tempValue * self.alpha

    def train(self, round):
        '''
        使用训练集进行训练
        :param round: 迭代次数
        :return:
        '''
        self.initalizeSubspace()
        for i in range(0, round):
            self.updateNoRegular()
            if i % 50 == 0:
                print("Round=" + str(i))
                print(f"MAE={self.MAE()}")

    def RSME(self):
        '''
        计算均方根误差
        :return: RSME
        '''
        resultRSME = 0.0
        for i in range(0, self.numRating):
            tempdata = self.dataset[i]
            tempUser, tempItem, tempRating = tempdata.user, tempdata.item, tempdata.rating
            tempPredict = self.predict(tempUser, tempItem)
            # 防止评分溢出
            if tempPredict > self.ratingHigh:
                tempPredict = self.ratingHigh
            elif tempPredict < self.ratingLow:
                tempPredict = self.ratingLow
            tempError = tempRating - tempPredict
            resultRSME += tempError * tempError

        return math.sqrt(resultRSME / self.numRating)

    def MAE(self):
        '''
        计算平均绝对误差
        :return: MAE
        '''
        resultMAE = 0.0
        for i in range(0, self.numRating):
            tempdata = self.dataset[i]
            tempUser, tempItem, tempRating = tempdata.user, tempdata.item, tempdata.rating
            tempPredict = self.predict(tempUser, tempItem)

            if tempPredict > self.ratingHigh:
                tempPredict = self.ratingHigh
            elif tempPredict < self.ratingLow:
                tempPredict = self.ratingLow
            tempError = tempRating - tempPredict

            resultMAE += abs(tempError)
        return resultMAE / self.numRating


if __name__ == '__main__':
    '''
    进行测试
    '''
    # 记录开始时间
    startTime = time.time()
    print(startTime)
    fileName = 'dataset/movielens-943u1682m.txt'
    # 初始化
    mf = MatrixFactorization(fileName, 943, 1682, 10000, 1, 5)
    mf.setParams(5, 0.0001, 0.005)
    # 开始训练
    print("Begin Training ! ! !")
    mf.train(2000)
    # 打印RSME MAE
    print("RSME=", mf.RSME())
    print("MAE=", mf.MAE())
    # 计算结束时间
    endTime = time.time()
    # 打印运行时间
    print("run :", 1000 * (endTime - startTime), "ms")

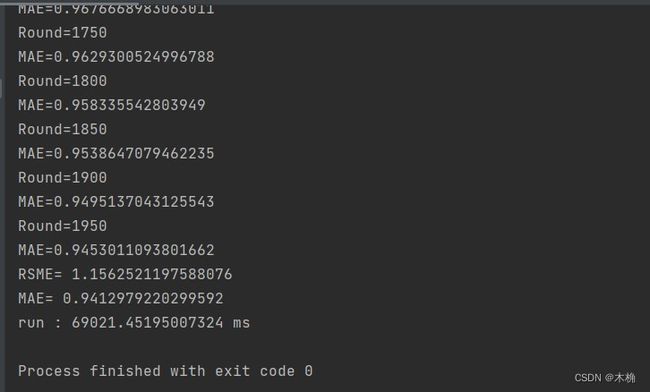
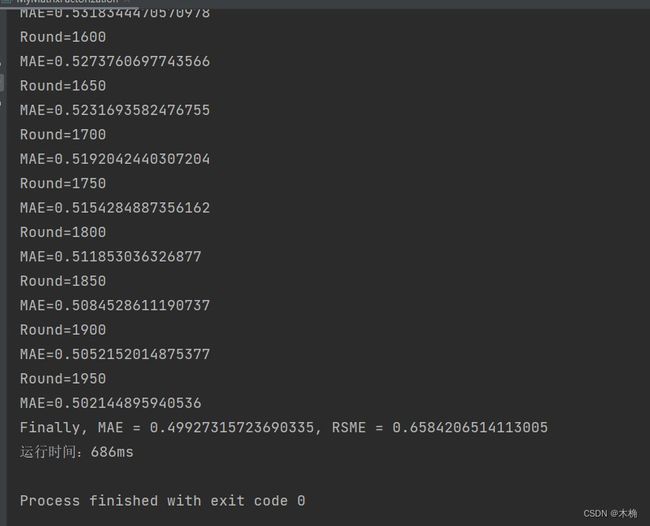
运行结果

可以看到python的运行时间是69秒

而java的运行时间远远小于python，只有686毫秒。

由此可见，python虽然组装时间快，但是运行速度确实更慢。