机器学习入门之PCA与ICA
文章目录
- 主成分分析 PCA
-
- 什么是降维
- PCA (Principal Component Analysis)
-
- 算法流程
- 独立成分分析 ICA
-
- 问题引入
- 算法
-
- 基于最大似然估计
- ICA的经典假设与不确定性
-
- 经典假设
- 不确定性
- ICA无法确定的因素
- 小结
本文为吴恩达机器学习课程的笔记系列第六篇,主要关于数据降维时常用的算法-PCA主成分分析算法,同时扩展另一算法-ICA 独立成分分析。
主成分分析 PCA
学习主成分分析之前,我们首先来了解什么是降维。
什么是降维
参考西瓜书的定义,降维即通过某种数学变换将原始高维属性空间转变为一个低维子空间。在这个子空间中样本密度大幅提高,距离计算也会变得更容易。
其实降维一般就是从高维投影到低维。
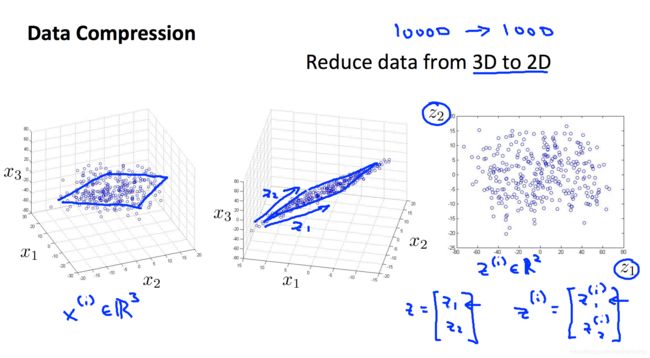
例如下图,对于3维数据,降到2维即是把数据从原来的3维空间投影到2维平面,这就实现了降维。
PCA (Principal Component Analysis)
主成分分析是最常见的降维算法。PCA 能从冗余特征中提取主要成分,在不太损失模型质量的情况下,提升了模型训练速度。
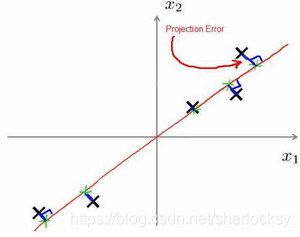
投影误差(Projection Error):
投影误差就是:把数据投影到一个经过原点的向量(即方向向量),此时的特征向量与该方向向量垂线的长度。
PCA的目标是,我们希望找到一个方向向量(Vector direction),使得这个投影误差的均方误差尽可能地小。
显然这是个降到一维的例子。那PCA的完整描述是:
想要将n维数据降至k维,那目标就是要找到这样的一组向量 u 1 , u 2 , u 3 , . . . , u k u_1,u_2,u_3,...,u_k u1,u2,u3,...,uk ,使得所有数据投影在这组向量上的总的投影误差最小。实际上这组向量在原始空间上应该是正交的。而这k维全新的正交特征也被称为主成分,是在原有n维特征的基础上重新构造出来的k维特征。
算法流程
-
均值归一化。
-
计算协方差矩阵:
Σ = 1 m ∑ i = 1 n ( x ( i ) ) ( x ( i ) ) T = 1 m X T X \Sigma = \dfrac{1}{m} \sum\limits_{i=1}^{n}(x^{(i)})(x^{(i)})^T = \dfrac{1}{m} X^TX Σ=m1i=1∑n(x(i))(x(i))T=m1XTX
-
通过奇异值分解计算协方差矩阵 Σ \Sigma Σ 的特征向量:
( U , S , V T ) = S V D ( Σ ) (U,S,V^T)=SVD(\Sigma) (U,S,VT)=SVD(Σ)
-
从 U U U 中选取前 k k k 个向量,获得一个 n × k n\times k n×k 维度的矩阵,用 U r e d u c e U_{reduce} Ureduce 表示。 k k k 的意思是我们希望将数据从 n n n 维降至 k k k 维。
-
计算新的特征向量 z ( i ) z^{(i)} z(i):
z ( i ) = U r e d u c e T ∗ x ( i ) z^{(i)}=U^T_{reduce} * x^{(i)} z(i)=UreduceT∗x(i)
显然,最终的结果自然是 k × 1 k \times 1 k×1 维度。
总的来说,想要得到主成分,先计算数据矩阵的协方差矩阵,再通过奇异值分解得到协方差矩阵的特征向量,然后选择特征值最大的也就是方差最大的k个特征向量组成的矩阵。
小结一下,PCA作为一个非监督学习的降维方法,它只需要特征值分解,就可以对数据进行压缩,去噪。因此在实际场景应用很广泛。
独立成分分析 ICA
上面的PCA是一个信息提取的过程,用于对原始数据进行降维,而接下来所提到的独立成分分析 即ICA(Independent Component Analysis),是一个信息解混的过程。
问题引入
ICA的前提是认为观察变量是若干个统计独立的分量的线性组合。
我们先从经典的鸡尾酒宴会问题(ocktail party problem)来讨论。这个问题是这样的:在一个房间里有 n n n 个人在开 party,他们可以同时说话。房间的不同角落里放置了 n n n 个声音接收器,每个接收器可以在每个时刻同时采集到 n n n 个人声音的重叠声音。每个接收器和每个人的距离是不一样的,所以每个接收器接收到的声音的重叠情况也不同。party结束后,我们得到 m m m 个声音样本,每个样本是在具体时刻 i i i,从 n n n 个接收器接采集的一组声音数据,如何从这 m m m 个样本集分离出 n n n 个说话者各自的声音呢?
我们仔细来看这个问题描述,用 s s s 来表示每个人在所有时刻所发出的声音信号源,它是一个 n × m n\times m n×m 的矩阵,每一行表示一个人 m m m 个时刻的声音信号序列,共 n n n 行,即 n n n 个人。
s = [ s 1 , s 2 , . . . , s n ] T s=[s_1,s_2,...,s_n]^T s=[s1,s2,...,sn]T
x x x 是每个时刻采样到的 n n n 个人的声音数据的线性组合。同样也是一个 n × m n\times m n×m 的矩阵。即有 m m m 个时刻,则共采样到 m m m 组样本,且每个样本都是 n n n 维的。这里的上标 i i i 表示的就是某个时刻, x i x^{i} xi 是一个分量,代表的就是 i i i 时刻接收到的所有人 n n n 个声音信号的线性组合。
x = [ ∣ ∣ … ∣ x ( 1 ) x ( 2 ) … x ( m ) ∣ ∣ … ∣ ] x ( i ) = [ x 1 ( i ) , x 2 ( i ) , . . . , x n ( i ) ] T x=\begin{bmatrix} |&|&\dots&|\\x^{(1)} & x^{(2)}&\dots&x^{(m)}\\|&|&\dots&|\end{bmatrix} \\ x^{(i)}=[x_1^{(i)},x_2^{(i)},...,x_n^{(i)}]^T x=⎣⎡∣x(1)∣∣x(2)∣………∣x(m)∣⎦⎤x(i)=[x1(i),x2(i),...,xn(i)]T
因此我们有如下模型:
x = A s [ ∣ ∣ … ∣ x ( 1 ) x ( 2 ) … x ( m ) ∣ ∣ … ∣ ] = A [ s 1 ( 1 ) s 1 ( 2 ) … s 1 ( m ) s 2 ( 1 ) s 2 ( 2 ) … s 2 ( m ) ⋮ ⋮ ⋱ ⋮ s n ( 1 ) s n ( 2 ) … s n ( m ) ] x=As\\ \begin{bmatrix} |&|&\dots&|\\x^{(1)} & x^{(2)}&\dots&x^{(m)}\\|&|&\dots&|\end{bmatrix}=A\begin{bmatrix} s_1^{(1)}&s_1^{(2)}&\dots&s_1^{(m)}\\s_2^{(1)}&s_2^{(2)}&\dots&s_2^{(m)}\\\vdots&\vdots&\ddots&\vdots \\s_n^{(1)}&s_n^{(2)}&\dots&s_n^{(m)}\end{bmatrix} x=As⎣⎡∣x(1)∣∣x(2)∣………∣x(m)∣⎦⎤=A⎣⎢⎢⎢⎢⎡s1(1)s2(1)⋮sn(1)s1(2)s2(2)⋮sn(2)……⋱…s1(m)s2(m)⋮sn(m)⎦⎥⎥⎥⎥⎤
其中, A A A 为未知的混合矩阵,显然 A A A 是 n × n n\times n n×n 维的,且必须满秩。
现在的情况就是 A 、 s A、s A、s 是未知的, x x x 是已知的,我们要想办法根据 x x x 来推出 s s s 和 A A A,这个过程也叫盲信号分离。这听上去有点amazing,我们下面慢慢来看。
算法
在不失一般性的情况下,我们可以假设混合变量和独立分量都具有零均值;如果原始数据不是 zero-mean,我们可以对观察变量 x x x 标准化,使得模型为零均值模型。
首先,我们做个变换,令 W = A − 1 W=A^{-1} W=A−1,那 s ( i ) = A − 1 x ( i ) = W x ( i ) s^{(i)}=A^{-1}x^{(i)}=Wx^{(i)} s(i)=A−1x(i)=Wx(i), W W W又可表示成 [ w 1 T , w 2 T , . . . , w n T ] T [w_1^T,w_2^T,...,w_n^T]^T [w1T,w2T,...,wnT]T,所以对每个源信号分量有:
s j ( i ) = w j T x ( i ) s_j^{(i)}=w^T_jx^{(i)} sj(i)=wjTx(i)
然后,我们假设每个人发出的声音信号 s j s_j sj 是独立的,并且存在着概率密度 p s ( s j ) p_s(s_j) ps(sj),那么给定时刻 i i i 源信号的联合概率密度为:
p ( s ) = ∏ j = 1 n p s ( s j ) p(s)=\prod_{j=1}^np_s(s_j) p(s)=j=1∏nps(sj)
有了 p ( s ) p(s) p(s),我们想得到采样信号的概率,那怎么求得呢?
我们先回忆概率论的知识,我们知道概率密度可由累积分布函数求导得到,那不妨先求一下累积分布函数:
F x ( a ) = P ( x ≤ a ) = P ( A s ≤ a ) = P ( s ≤ W a ) = F s ( W a ) F_x(a)=P(x\le a)=P(As\le a)=P(s\le Wa)=F_s(Wa) Fx(a)=P(x≤a)=P(As≤a)=P(s≤Wa)=Fs(Wa)
接着求个导:
F x ′ ( a ) = F s ′ ( W a ) = ∣ W ∣ p s ( W a ) = p x ( a ) F'_x(a)=F'_s(Wa)=|W|p_s(Wa)=p_x(a) Fx′(a)=Fs′(Wa)=∣W∣ps(Wa)=px(a)
所以有:
p ( x ) = p s ( W x ) ∣ W ∣ = ∣ W ∣ ∏ j = 1 n p s ( w j T x ) p(x)=p_s(Wx)|W|=|W|\prod_{j=1}^np_s(w_j^Tx) p(x)=ps(Wx)∣W∣=∣W∣j=1∏nps(wjTx)
基于最大似然估计
似然函数:
L ( W ) = p s ( W x ) ∣ W ∣ = ∣ W ∣ ∏ j = 1 n p s ( w j T x ) L(W)=p_s(Wx)|W|=|W|\prod_{j=1}^np_s(w_j^Tx) L(W)=ps(Wx)∣W∣=∣W∣j=1∏nps(wjTx)
给定训练样本 x ( i ) = ( x ( 1 ) , x ( 2 ) , . . . , x ( m ) x^{(i)}=(x^{(1)},x^{(2)},...,x^{(m}) x(i)=(x(1),x(2),...,x(m) ,求对数似然:
l n L ( W ) = ∑ i = 1 m { ∑ j = 1 n l n p s ( w j T x ( i ) ) + l n ∣ W ∣ } lnL(W)= \sum_{i=1}^m\{ \sum_{j=1}^nln\;p_s(w^T_jx^{(i)})+ln|W|\} lnL(W)=i=1∑m{j=1∑nlnps(wjTx(i))+ln∣W∣}
ICA的经典假设与不确定性
经典假设
1.各个成分之间是相互独立的
这是ICA的一个最基本也是最重要的原则,非常有趣的是一旦给出了这个假设,我们便可以通过一定的方式求解这个模型。对此的解释是,如果任意的随机变量序列(x1,x2,…,xn)之间是相互统计独立的,则这就意味着我们不能从其余的变量中获得随机变量xj的任何信息。
2.ICA非常强的一个假设:独立成分是服从非高斯分布的。
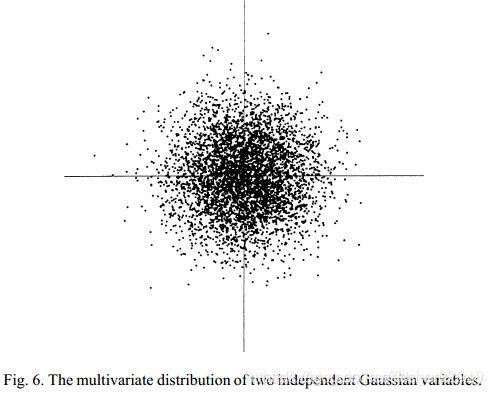
这是因为,如果源信号是高斯的,也就是独立成分都是高斯的,那么他们的联合概率分布将是均匀的,密度是完全对称的,如下图的二维高斯分布为例。外面可以看到,高斯变量 ( x 1 , x 2 ) (x_1,x_2) (x1,x2) 的任何正交变换的分布具有与 ( x 1 , x 2 ) (x_1,x_2) (x1,x2) 完全相同的分布。因为高斯分布的随机变量有着高阶累积量为0的特性,所以ICA所做分解后的A可能有无穷多个。
如果源信号是非高斯的,那么ICA所做的分解是唯一的。这也是为什么一般在标准的独立成分分析中最多只允许有一个成分服从高斯分布。
3.假设混合矩阵A是方阵
这个很明显,是为了使得A可逆,方便计算。
不确定性
具备相同统计特征的 x x x 可能来自两个不同的系统:
x = A s = ( A α ) ( α − 1 s ) x=As=(A\alpha)(\alpha^{-1}s) x=As=(Aα)(α−1s)
也可以理解为采样信号与噪声信号具有不可辨识性 nonidentifiable。上式子可以发现,经过一个线性变换,混合矩阵A和s就变得不是唯一的了,所以我们也是无法唯一确定原信号。
ICA无法确定的因素
- 不能确定独立成分的方差
- 不能确定独立成分的顺序
小结
不管是PCA还是ICA,都不需要你对源信号的分布做具体的假设。
如果观察到的信号是高斯的,那么此时源信号也是高斯的,这时PCA和ICA是等价的。
大多数ICA的算法需要进行数据预处理:先用PCA得到y,再把y的各个分量标准化(即让各分量除以自身的标准差)得到z。预处理后得到的z满足下面性质:
- z的各个分量不相关;
- z的各个分量的方差都为1。
上一篇文章地址:机器学习入门之聚类算法
下一篇文章地址:机器学习入门之异常检测