Matplotlib和Seaborn（离散数据的图表选择与一些使用技巧）

为离散数据选择图表

如果想要绘制离散型数值变量，直方图或条形图都是可能的选择 。

直方图可能是最直接的选择，因为数据是数值型的，但是需要特别考虑一下分组边界的问题。因为离散型数值都是特定的值，而你的读者可能并不了解分组边界的值属于右边的分组，所以将分组边界设置为实际的两个值之间可以减少歧义。请比较下面两个图表，图表的数据是 100 次随机掷骰结果（die_rolls），左图是分组边界值等于数据实际值的情况，右边是分组边界在数据实际值之间的情况。

plt.figure(figsize = [10, 5])

# histogram on the left, bin edges on integers
plt.subplot(1, 2, 1)
bin_edges = np.arange(2, 12+1.1, 1) # note `+1.1`, see below
plt.hist(die_rolls, bins = bin_edges)
plt.xticks(np.arange(2, 12+1, 1))

# histogram on the right, bin edges between integers
plt.subplot(1, 2, 2)
bin_edges = np.arange(1.5, 12.5+1, 1)
plt.hist(die_rolls, bins = bin_edges)
plt.xticks(np.arange(2, 12+1, 1))

你会注意到左侧的直方图在设置分组边界时，我在最大值（12）的基础上加了 1.1，而不是 1。回想一下前面讲的内容，最右侧的边界会落在最后一个分组内，如果数据中包含很多个最大值，它们都会落在左边属于数据值 11 的分组内，这个潜在问题对于离散型数值尤其需要注意。为最大值加上 1.1，可以让 12 这个值单独存放在最后一个分组内，避免 11 和 12 在同一个分组。

考虑一下长条不相连的条形图是否可以成为替代直方图的更好方案。 以下的图表采用了之前的代码，只是添加了 “rwidth” 参数，用来设置每个直方图长条占各自宽度的比例。将 “rwidth” 参数设置为 0.7，长条只会占据原本分组条形空间的 70%，左侧留出 30% 的空白。

bin_edges = np.arange(1.5, 12.5+1, 1)
plt.hist(die_rolls, bins = bin_edges, rwidth = 0.7)
plt.xticks(np.arange(2, 12+1, 1))

通过在长条之间增加空隙，强调数据的值是离散的。但另一方面，以这种方式绘制数值型数据可能会被理解为数据是有序分类数据，这样会对整体的理解带来影响。

==对于连续型数据，最好不要使用 “rwidth” 参数，因为长条的空隙暗示数值是离散的。==另外注意，你可能会尝试使用 seaborn 的 countplot 函数将离散数值变量的分布情况绘制成条形图。这样操作时要小心，因为无论两个值之间的间距多大，每个唯一数 值都对应一个长条（比如，如果唯一值为 {1,2,4,5}，缺少了 3，那么 countplot 只会绘制 4 个条形，其中 2 和 4 相邻）。此外，即使数据是离散数字，也尽量不要考虑此页面上描述的直方图变体版本，除非唯一值的数量很小，允许半个单位的位移使离散长条可解释。如果有大量唯一值并且分布在很大的范围内，则最好采用标准直方图，避免出现解释性问题的风险。

虽然你可以使用条形图绘制离散数据，但你很难充分地解释以下情况，即：将有序分类数据绘制为直方图。条形图中长条之间的空隙会提醒读者，值不是连续的，属于一种 “间隔” 形式：只是级别是有序的。如果删除空隙后，则很难记得这一点。

描述统计量、异常值和坐标轴范围

在创建图表和探索数据时，不要只关注描述统计量传达的信息，也要确保关注图形传递的其他信息，例如峰的数量和偏态，注意数据中是否有任何异常值以供进一步的研究。

由于可能存在的异常值，你可能需要更改坐标轴的范围或标尺，从而观察数据的底层规律。本节课会介绍更改坐标轴范围的内容，下节课会介绍坐标轴的标尺变换。要更改直方图的坐标轴范围，你可以在代码中调用 Matplotlib 的 xlim 函数。该函数接受一个包含两个数字的元组，用于指定 x 轴的上限和下限。或者，也可以在 xlim 函数中直接传入两个数字参数，两者效果一样。

plt.figure(figsize = [10, 5])

# histogram on left: full data
plt.subplot(1, 2, 1)
bin_edges = np.arange(0, df['skew_var'].max()+2.5, 2.5)
plt.hist(data = df, x = 'skew_var', bins = bin_edges)

# histogram on right: focus in on bulk of data < 35
plt.subplot(1, 2, 2)
bin_edges = np.arange(0, 35+1, 1)
plt.hist(data = df, x = 'skew_var', bins = bin_edges)
plt.xlim(0, 35) # could also be called as plt.xlim((0, 35))

在上述示例中，我们可能会想要比较小于 35 的数据模式和大于 35 的数据模式。对于集中在前一组（<35）的数据，我们无需滤除掉所有大于 35 的数据创建新的 DataFrame，只通过设定坐标轴范围就可以重点关注了 。

标尺和变换

某些数据分布可以进行标尺变换。最常见的示例是近似符合对数正态分布的数据。这样的数据采用原始单位的话，看起来非常偏态：很多数据点的值很小，有很长的尾部，而且尾部数据点的值很大，但是取对数的话，数据看起来就像是正态分布的。

plt.figure(figsize = [10, 5])

# histogram on left: natural units
plt.subplot(1, 2, 1)
bin_edges = np.arange(0, ln_data.max()+100, 100)
plt.hist(ln_data, bins = bin_edges)

# histogram on right: directly log-transform data
plt.subplot(1, 2, 2)
log_ln_data = np.log10(ln_data)
log_bin_edges = np.arange(0.8, log_ln_data.max()+0.1, 0.1)
plt.hist(log_ln_data, bins = log_bin_edges)
plt.xlabel('log(values)') # add axis label for clarity

在左图中，值大于 1000 的少部分数据将大部分数据点推到了最左侧的分组中。对于右图，对数变换将这些大的数据点分布看起来和剩余的数据点比较一致：原始值 1000 在对数变换下变成了对数值 3，原始值 100 被变换为对数值 2。右图的最大问题是 x 轴的单位很难解释：对于很多人来说，只能简单地将整数的对数值转换为原始值（假设基数是示例中10 这样比较好计算的值）。

这时候标尺变换就派上用场了。在标尺变换中值的间隙基于变换后的比例，但是你可以用变量的原始单位解释数据。此外，你不需要设定新的特征变量，这很方便。Matplotlib 的 xscale 函数包含几个内置的变换：我们将在这里尝试使用 “对数” 标尺。

bin_edges = np.arange(0, ln_data.max()+100, 100)
plt.hist(ln_data, bins = bin_edges)
plt.xscale('log')

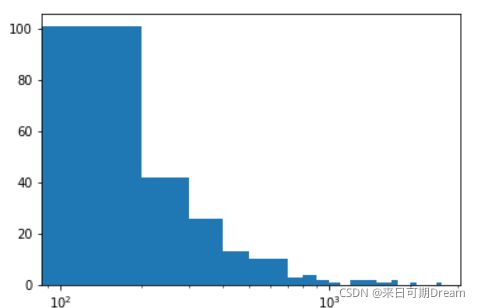对于现在这个图表，注意两点：首先，即使数据采用的是对数标尺，组区间依然呈线性分布，意味着它们的尺寸从左到右由宽变窄，因为值会成倍增大。其次，默认的标签设置依然很难解释，并且很稀疏 。

要处理组宽的尺寸问题，我们只需将它们变成 10 的幂次方并且均匀分布。根据你所绘制的数据，2 或者其他值的幂次方可能更合适。对于刻度，我们可以使用 xticks 函数，以原始单位指定位置和标签。注意：我们并没有更改数据的值，只是改变了显示方式。在 10 的幂次方的整数之间，我们没有表示均匀刻度的整数，但是可以很接近。对于 10 幂次方对数变换，设置 1-3-10 或 1-2-5-10 这样的循环刻度很有用。

bin_edges = 10 ** np.arange(0.8, np.log10(ln_data.max())+0.1, 0.1)
plt.hist(ln_data, bins = bin_edges)
plt.xscale('log')
tick_locs = [10, 30, 100, 300, 1000, 3000]
plt.xticks(tick_locs, tick_locs)

请务必在 xscale 之后指定 xticks，因为该函数具有内置的刻度设置

最终，我们获得了和进行直接对数变换的图表一样的图表，但是现在的刻度和标签看起来美观多了。

替代方法

注意，对数变换并不是唯一的变换方式。在进行对数变换时，数据值必须全是正数， 0 或负数无法取对数。此外，对数变换后，对对数标尺进行加法将导致原始标尺出现倍数变化，这是在数据建模时需要注意的重要事项。你可以根据数据判断该选择什么类型的变换。

如果你想使用 xscale 中未提供的其他变换，则需要进行某些特征工程。在这种情形下，我们需要写一个应用变换和还原过程的函数，以保持系统性。当我们想要将变换了的数值变回到原始单位的时候，还原功能就很有用。为了进行演示，假设我们想要以平方根变换的形式绘制上述数据（或许这些数字表示面积，我们认为有必要按照半径、长度或其他一维近似值来对数据建模）。我们可以如下所示地绘制变换后的分布情况：

def sqrt_trans(x, inverse = False):
    """ transformation helper function """
    if not inverse:
        return np.sqrt(x)
    else:
        return x ** 2

bin_edges = np.arange(0, sqrt_trans(ln_data.max())+1, 1)
plt.hist(ln_data.apply(sqrt_trans), bins = bin_edges)
tick_locs = np.arange(0, sqrt_trans(ln_data.max())+10, 10)
plt.xticks(tick_locs, sqrt_trans(tick_locs, inverse = True).astype(int))

注意 ln_data 是一个 pandas Series，因此我们可以使用该函数的 apply 方法来应用该函数。如果是 NumPy 数组，则需要像在其他情形下一样应用该函数。刻度位置同样应该用原始值指定，所以我们对 xticks 的第一个参数应用了该变换函数。

核密度估计：

在之前，通过使用 seaborn 的 distplot 函数见到了核密度估计（KDE）示例，该函数在直方图上绘制了 KDE。
sb.distplot(df[‘num_var’])

核密度估计是***估计变量的概率密度函数***的一种方式。在 KDE 图表中，你可以将每个观测值看做一个小的块状区域。将这些块状区域都堆叠到一起可以生成最终的密度曲线。默认设置使用正态分布内核，但是能够生成 KDE 图形的大部分软件还包括其他内核函数选项。

Seaborn 的 distplot 函数会调用另一个函数 kdeplot 来生成 KDE。以下演示代码还使用了被 distplot 调用的第三个函数 rugplot。在轴须图（rugplot）中，数据点被描绘成数值轴上的短竖线 。

data = [0.0, 3.0, 4.5, 8.0]
plt.figure(figsize = [12, 5])

# left plot: showing kde lumps with the default settings
plt.subplot(1, 3, 1)
sb.distplot(data, hist = False, rug = True, rug_kws = {'color' : 'r'})

# central plot: kde with narrow bandwidth to show individual probability lumps
plt.subplot(1, 3, 2)
sb.distplot(data, hist = False, rug = True, rug_kws = {'color' : 'r'},
            kde_kws = {'bw' : 1})

# right plot: choosing a different, triangular kernel function (lump shape)
plt.subplot(1, 3, 3)
sb.distplot(data, hist = False, rug = True, rug_kws = {'color' : 'r'},
            kde_kws = {'bw' : 1.5, 'kernel' : 'tri'})

根据这种图表解释概率比标准直方图稍微复杂些。纵轴表示的是数据密度，而不是直接的概率。在 KDE 图表中，x 坐标轴和曲线之间的总面积为 1。位于两个值之间的概率可以通过计算这两个值之间的曲线下方面积得出。不借助计算机判断面积大小很难，也很可能不准确。

虽然通过 KDE 做出具体的概率判断没有直方图直观，但是使用核密度估计依然存在一定的理由。==如果数据点相对较少，则 KDE 可以对整体数据分布提供平滑的估计。==这些信息可能无法通过直方图轻松地呈现出来，大量的不连续跳跃性数据，在直方图中可能会造成误导。

另外要注意的是，KDE 中的带宽参数（bandwidth）会指定密度块体的宽度是多少。和直方图的组距（bin_width）类似，我们需要选择最能表示数据规律的带宽大小。带宽太小的话，数据看起来比实际的噪点更多，带宽太大的话，可能会遮蔽数据的有用特征。记住有这个设置方法，以防可视化软件所选的默认带宽看起来不太合适，或者你想要进一步展开调查。