【数据压缩】第六次作业—— DPCM压缩系统的实现和分析

DPCM压缩系统的实现和分析

实验原理

DPCM编解码原理

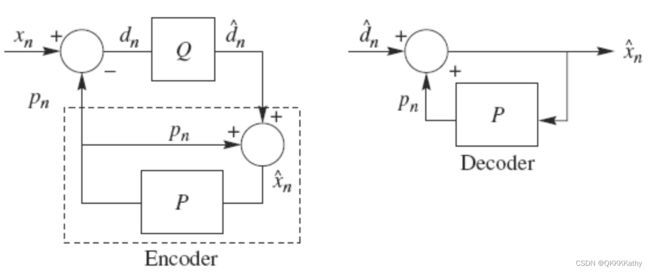
DPCM是差分预测编码，它是一个负反馈系统，其编解码原理如下图所示：

DPCM利用信源相邻符号之间的相关性进行预测编码。在编码端，输入一个样本值，与上一个样本的预测值作差，对差值进行量化，得到的量化结果一方面作为编码端输出，另一方面反量化后作为预测器的输入，与上一个样本的预测值相加，作为当前样本的预测值（或说重建值）。

可以看到，DPCM在编码端内嵌了一个解码器，这是因为在解码端没有办法得到原始样本，只能得到样本的重建值，因此在编码端内嵌解码器的方法可以减小误差。

量化

DPCM对当前像素值与预测值相减得到的误差值进行量化，误差值的范围在[-255,255]之间，需要用9bit表示，同时，为了使得预测误差范围均为正值，所以要对误差值+255之后再进行量化。因此，对于nbit量化，量化后误差值的计算公式为：（原始误差值+255）/2^(9-n)。

PSNR峰值信号噪声比

PSNR是一种评价图像的客观标准，给定大小为$M\times N$的两幅图像来说，其PSNR值为$PSNR=10\cdot {\log }_{10}(\frac{x_{max}^2}{MSE})$，其中MSE是指均方误差，其计算公式为$MSE=\frac{1}{M\times N}\sum _{m=0}^{M-1}\sum _{n=0}^{N-1}[x(m,n)-\hat{x}(m,n){]}^2$，$x(m,n)$和$\hat{x}(x,n)$分别表示两幅图像在点$(m,n)$处的像素值

PSNR是基于对应像素点间的误差，即基于误差敏感的图像质量评价，但是并没有考虑人眼的视觉特性，因而经常出现评价结果与人的主观感受不一致的情况。

PSNR高于40dB说明图像质量极好，即非常接近原始图像；

PSNR在30~40dB通常表示图像质量是好的，即失真可以察觉但是可以接受；

PSNR在20~30dB说明图像质量差；

PSNR低于20dB的图像通常不可以被接受。

实验代码分析

BMP2YUV

利用之前写过的BMP2YUV程序将样例图片转换成yuv格式，并命名为xxxx_origin.yuv代表输入的原始图像

另外，除了Birds_origin.yuv的大小是768×512以外，其余所有图片大小均为256×256

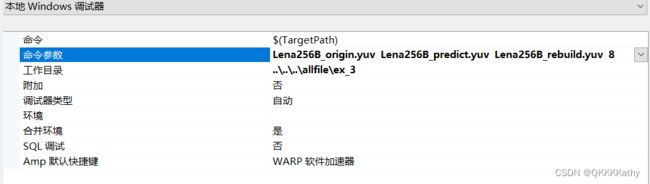
设置命令行参数

设置命令行参数，分别为原始图像origin、预测误差图predict、重建图像rebuild和量化比特数

关键代码分析

DPCM计算

• 本次实验采用左侧预测，并假设第一列的预测值为128
• 实验中分别计算了8bit量化、4bit量化、2bit量化和1bit量化的预测误差和重建图像，并对原图和重建图像进行了比较
• 实验还尝试了对位深为4的图片进行了DPCM预测编解码，并得到重建图，与原图进行比较
• 实验结束后，对原图和预测误差图分别进行霍夫曼压缩编码，查看编码效率，同时分别统计原图和预测误差图的概率分布

int Quant(int qbit, int error) {    //量化
	int k = 0;
	k = ((error + 255) / pow(2, (9 - qbit)));    //+255将误差值抬为正值再做量化
	return k;
}

int inverseQuant(int qbit, unsigned char pred) {   //反量化
	int k = 0;
	k = (pred * pow(2, (9 - qbit)) - 255);
	return k;
}

void DPCM(unsigned char* y_buffer, unsigned char* pred_buffer, unsigned char* re_buffer, int width, int height, int qbit) {
	int error;

	for (int i = 0; i < height; i++) {
		for (int j = 0; j < width; j++) {
			if (j == 0) {    //第一列以128进行预测
				error = (y_buffer[i * width + j]) - 128;     //误差值
				pred_buffer[i * width + j] = Quant(qbit, error);     //量化误差值
				re_buffer[i * width + j] = inverseQuant(qbit, pred_buffer[i * width + j]) + 128;    //重建值
			}
			else {   //其他列都以前一列进行预测
				error = (y_buffer[i * width + j]) - re_buffer[i * width + j - 1];    //误差值
				pred_buffer[i * width + j] = Quant(qbit, error);    //量化误差值
				re_buffer[i * width + j] = inverseQuant(qbit, pred_buffer[i * width + j]) + re_buffer[i * width + j - 1];    //重建值
			}
		}
	}

	int max = pow(2, qbit) - 1;    //当前量化的最大值

	for (int i = 0; i < width * height; i++) {     //处理可能溢出的情况
		if (pred_buffer[i] < 0) pred_buffer[i] = 0;
		if (pred_buffer[i] > max) pred_buffer[i] = max;   
		if (re_buffer[i] < 0) re_buffer[i] = 0;
		if (re_buffer[i] > 255) re_buffer[i] = 255;
	}

}

PSNR计算

计算重建图与原始图的PSNR值，对图片质量进行评价

double PSNR(unsigned char* y_buffer, unsigned char* re_buffer,int width, int height, int qbit) {
	double mse = 0, psnr = 0;
	for (int i = 0; i < width * height; i++) {
		mse += pow((y_buffer[i] - re_buffer[i]), 2);
	}
	mse = mse / (width * height);
	psnr = 10 * log10(pow(255, 2) / mse);
	return psnr;
}

主程序

打开图像文件并读取像素值，统计原图像的概率分布和量化后的预测误差图的概率分布

void Frequency(unsigned char* buffer, double* frequency, int height, int width)    //计算概率
{
	int size = height * width;
	for (int i = 0; i < size; i++) frequency[buffer[i]] += 1;
	for (int i = 0; i < 256; i++) frequency[i] /= size;
}

int main(int argc, char** argv) {
	
	char* ori_name = argv[1];     //原始图像
	char* pred_name = argv[2];    //预测误差图像
	char* re_name = argv[3];    //重建图像
	int qbit = atoi(argv[4]);   //量化bit数

	FILE* ori_file = NULL;     //原始yuv
	FILE* pred_file = NULL;     //预测误差yuv
	FILE* re_file = NULL;      //重建yuv

	int width = 256, height = 256;   //除了birds以外所有图片都是256*256的

	//int width = 768, height = 512;   //birds

	unsigned char* y_buffer = new unsigned char[width * height];
	unsigned char* u_buffer = new unsigned char[(width * height) / 4];
	unsigned char* v_buffer = new unsigned char[(width * height) / 4];     //原始图像的yuv
	unsigned char* pred_buffer = new unsigned char[width * height];  //预测误差图像buffer
	unsigned char* re_buffer = new unsigned char[width * height];    //重建图像buffer

	ori_file = fopen(ori_name, "rb");
	if (ori_file == NULL) {
		cout << "Can't open the origin image!" << endl;
	}
	else {
		cout << "The origin image has been opened!" << endl;
	}

	pred_file = fopen(pred_name, "wb");
	if (pred_file == NULL) {
		cout << "Can't open the predict image!" << endl;
	}
	else {
		cout << "The predict image has been opened!" << endl;
	}

	re_file = fopen(re_name, "wb");
	if (re_file == NULL) {
		cout << "Can't open the rebuild image!" << endl;
	}
	else {
		cout << "The rebild image has been opened!" << endl;
	}

	//unsigned char* uv_buffer = new unsigned char[(width * height) / 2];     //用来处理birds
	//for (int i = 0; i < (width * height) / 2; i++) {
	//	uv_buffer[i] = 128;
	//}

	//读原文件
	fread(y_buffer, 1, width * height, ori_file);
	fread(u_buffer, 1, (width * height) / 4, ori_file);
	fread(v_buffer, 1, (width * height) / 4, ori_file);

	FILE* orig;     //计算原文件的概率分布
	orig = fopen("E:/biancheng/c and c++/data compression/allfile/ex_3/Lena256B_origin.txt", "wb");
	double frequency[256] = { 0 };
	Frequency(y_buffer, frequency, height, width);
	fprintf(orig, "%s\t%s\n", "symbol", "freq");
	for (int i = 0; i < 256; i++)
	{
		fprintf(orig, "%d\t%f\n", i, frequency[i]);
	}

	//DPCM
	DPCM(y_buffer, pred_buffer, re_buffer, width, height, qbit);

	//计算PSNR
	double psnr;
	psnr = PSNR(y_buffer, re_buffer, width, height, qbit);
	cout << "The PSNR of " << ori_name << " is " << psnr << endl;

	//写预测误差文件
	fwrite(pred_buffer, 1, width * height, pred_file);
	fwrite(u_buffer, 1, (width * height) / 4, pred_file);
	fwrite(v_buffer, 1, (width * height) / 4, pred_file);

	//	//写预测误差文件
	//fwrite(pred_buffer, 1, width * height, pred_file);
	//fwrite(uv_buffer, 1, (width * height) / 2, pred_file);     //处理birds

	FILE* pred;   //计算预测误差文件的概率分布
	pred = fopen("E:/biancheng/c and c++/data compression/allfile/ex_3/Lena256B_predict_1bit.txt", "wb");
	double frequency_[256] = { 0 };
	Frequency(pred_buffer, frequency_, height, width);
	fprintf(pred, "%s\t%s\n", "symbol", "freq");
	for (int i = 0; i < 256; i++)
	{
		fprintf(pred, "%d\t%f\n", i, frequency_[i]);
	}


	//写重建图像文件
	fwrite(re_buffer, 1, width * height, re_file);
	fwrite(u_buffer, 1, (width * height) / 4, re_file);
	fwrite(v_buffer, 1, (width * height) / 4, re_file);


	fclose(ori_file);
	fclose(pred_file);
	fclose(re_file);

	delete[] y_buffer;
	delete[] u_buffer;
	delete[] v_buffer;
	delete[] pred_buffer;
	delete[] re_buffer;
	//delete[] uv_buffer;

	return 0;

}

实验结果分析

压缩质量

量化比特数	原图	预测误差图	重建图	PSNR
8				51.1422
8				51.1347
8				51.1338
8				51.1538
8				51.1239
8				51.1417
8				51.1338
4				14.8189
2				7.64999
1				7.59892
8				51.1416
4				10.208

通过实验可以看出来，使用8bit量化可以较好地还原原始图像，此时得到的PSNR值都在50以上，也就说明图像质量极好，接近原始图像，人眼几乎无法看出异常。随着量化bit数减少，PSNR值也逐渐降低，图像出现了明显的失真，已经无法很好的重建图像了

Huffman编码效率

采用“压缩比=压缩前所占空间大小/实际所占空间大小”计算

原始图像	原始图像大小(KB)	直接熵编码大小(KB)	直接熵编码压缩比	量化器量化比特数	预测误差图像大小(KB)	DPCM+熵编码大小(KB)	DPCM+熵编码压缩比
Clown256B	96	74	1.297	8	96	48	2.000
Zone256B	96	63	1.524	8	96	72	1.333
Noise256B	96	68	1.412	8	96	73	1.315
Birds	576	520	1.108	8	576	192	3.000
Lena256B	96	69	1.391	8	96	46	2.087
Lena256B	96	69	1.391	4	96	24	4.000
Lena256B	96	69	1.391	2	96	23	4.174
Lena16B	96	17	5.647	8	96	20	4.800
Lena16B	96	17	5.647	4	96	23	4.174

可以看到，对于大多数图像来说，经过DPCM预测编码之后，误差图像的压缩效率有了明显的提高，并且随着量化比特数的减小，压缩效率也会升高，只是重建图像的质量就会很差。

不过对Noise256B和Zone256B两张图片来说，使用DPCM预测编码后压缩效率并没有提高。这可能是因为预测编码是利用相邻信源之间的相关性进行的，相邻像素之间的相关性越大，预测就会更加准确，而Noise256B和Zone256B这两张图片在水平方向上相邻像素点的灰度值变化很大，所以DPCM并没有发挥很好的效果。

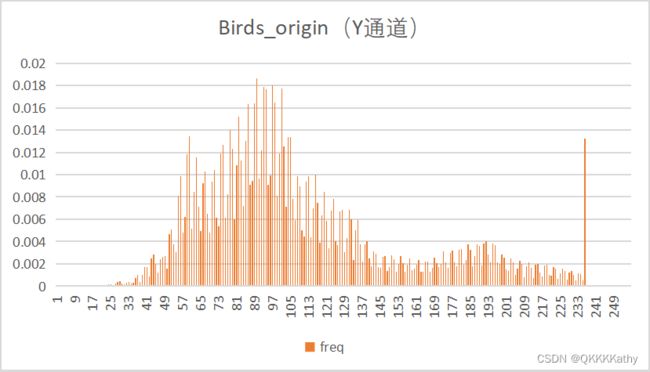
原始图像与预测误差图概率分布

图像	概率分布
Clown256B_origin
Clown256B_predict_8bit
Zone256B_origin
Zone256B_predict_8bit
Noise256B_origin
Noise256B_predict_8bit
Birds_origin
Birds_predict_8bit
Lena256B_origin
Lena256B_predict_8bit
Lena256B_predict_4bit
Lena256B_predict_2bit
Lena16B_origin
Lena16B_predict_8bit
Lena16B_predict_4bit

通过观察各个图像的概率分布图可以发现，利用DPCM得到的预测残差图的概率分布近似为Laplacian分布，更适合用霍夫曼编码，因此预测误差图的压缩效率更高。

而对于位深为4bit的图片来说，可以观察到本身的像素取值就不是很多，猜测这可能是导致位深为4bit的原图的压缩效率也较高的原因。

实验总结

• 在实验开始的时候总是碰到下面的问题：

经检查是因为在打开pred_file之后对其进行了判断，判断时误将==写成了=，使得文件变为了NULL，所以一直没能写进去内容

• 对于4bit、2bit、1bit量化的情况，因为量化后电平较低，所以可能没有办法看清预测误差图像，因此可以将电平抬高128观察

• 实验中发现利用霍夫曼编码得到的符号概率和自行统计的符号概率有些区别，后面需要进一步探究原因

• 对于相邻符号之间相关性较高的图片来说，DPCM可以很好的利用这一特性，减少冗余度，提高编码效率