论文阅读笔记(9):加权稀疏子空间表示——子空间聚类、约束聚类和主动学习的统一框架
论文阅读笔记(9):WEIGHTED SPARSE SUBSPACE REPRESENTATION——A UNIFIED FRAMEWORK FOR SUBSPACE CLUSTERING, CONSTRAINED CLUSTERING, AND ACTIVE LEARNING, 加权稀疏子空间表示——子空间聚类、约束聚类和主动学习的统一框架
- 摘要
- 1. 介绍
- 2. 相关工作
-
- 线性子空间聚类
- 基于谱方法的子空间聚类
- 约束聚类和主动学习
- 3. 加权稀疏单纯形表示
加权稀疏子空间表示——子空间聚类、约束聚类和主动学习的统一框架
这篇文章的related work写得非常详细
摘要
在这项工作中,我们首先提出了一种新的基于谱的子空间聚类算法,该算法试图将每个点表示为几个相邻点的稀疏凸组合。然后,我们将该算法扩展到约束聚类和主动学习。我们开发这样一个框架的动机源于这样一个事实,即通常可以提前获得少量标记数据;或者,有可能以很少的成本标记某些点。后一种情况通常在验证集群分配的过程中遇到。在模拟数据集和真实数据集上的大量实验表明该方法是有效的。
1. 介绍
在许多涉及高维数据分组的具有挑战性的实际应用中,不同的簇可以很好地近似为低维子空间。例如,基因测序(McWilliams和Montana,2014年)、人脸聚类(Elhamifar和Vidal,2013年)、运动分割(Rao等人,2010年)和文本挖掘(Peng等人,2018年)就是如此。同时估计每个簇对应的子空间并根据这些子空间将一组点划分为簇的问题称为子空间聚类(Vidal,2011)。
用于子空间聚类的谱方法在许多实际应用中表现出优异的性能。这些方法通过解决优化问题来构造谱聚类的affinity矩阵,该优化问题旨在通过来自同一子空间的其他点的线性组合来近似每个点。在本文中,我们首先提出了一种称为加权稀疏单纯形表示(WSSR)的方法。该方法基于稀疏单纯形表示(SSR),其中每个点通过其他点的凸组合进行近似。该方法最初并不是作为子空间聚类方法提出的,而是用于模拟大脑解剖和遗传网络。我们修改了SSR,以确保每个点通过邻近邻域的稀疏凸组合来逼近,从而得到一种有效的子空间聚类算法。
由于完全缺乏标记数据,聚类方法很少达到完美的性能。在通常情况下,可以提前获得少量数据,也可以以一定的成本获得少量数据。聚类算法应当能够适应此有标签外的部信息(约束聚类)。更有趣的是,在主动学习环境中,选择要标记的点是学习问题的一部分。在这种情况下,算法应选择查询点的标签,以最大限度地提高整体模型的质量。在这项工作中,我们提出了一个用于WSSR的迭代主动学习和约束聚类框架。选择信息点进行子空间聚类查询。获取这些点的标签后,将更新聚类的指派。我们提出的约束聚类方法保证生成与所有可用标签一致的分配。
2. 相关工作
线性子空间聚类
线性子空间聚类问题可以定义如下。N个数据点的集合 X = { x i } i = 1 N ⊂ R P \mathcal X=\{x_i\}_{i=1}^N⊂\mathbb R^P X={xi}i=1N⊂RP是从 K K K个线性子空间 { S k } k = 1 K \{\mathcal S_k\}^K_{k=1} {Sk}k=1K和附加噪声的并中提取的。每个子空间可以定义为:
Vk∈RP×Pk,Pk<P![]()
其中矩阵 V k ∈ R P × P k , P k < P V_k\in \mathbb R^{P\times P_k},P_k
- 找到 K K K个子空间
- 找到这 K K K个子空间的维数 { P k } k = 1 K \{P_k\}^K_{k=1} {Pk}k=1K和组成该空间的基 { V k } k = 1 K \{V_k\}^K_{k=1} {Vk}k=1K
- 最后把 X \mathcal X X中的每个数据点分配到上述子空间 S k \mathcal S_k Sk中
这个问题最原始的优化目标可以被描述为最小化重构误差:
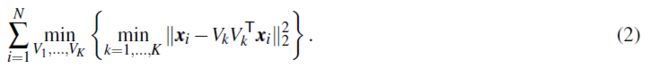
k k k-子空间聚类(KSC)是一种迭代算法,用于解决(2)中的问题。与经典的 K K K-means聚类一样,KSC在估计子空间的基(给定的聚类分配)和为将点指派到聚类中(给定的基集)之间进行交替。然而,迭代算法对初始化非常敏感,通常会收敛到较差的局部极小值(Lipor和Balzano,2017)。
基于谱方法的子空间聚类
目前,子空间聚类最有效的方法是基于谱的方法。基于谱的方法包括两个步骤:首先估计affinity矩阵,然后对该affinity矩阵应用归一化谱聚类。affinity矩阵是通过利用自表达特性,这需要首先解决一个凸优化问题:

上述公式我们十分熟悉,前一项是用affinity线性表出后的重构误差,后一项则是稀疏表示的罚函数。
最小二乘回归(LSR)使用L2范数表示近似重构误差和正则项。平滑表示聚类(SMR)也在近似误差上使用L2范数,而惩罚项由 ∣ ∣ L 1 / 2 β i ∣ ∣ 2 2 ||L^{1/2}β_i||_2^2 ∣∣L1/2βi∣∣22 其中L是由成对相似性构造的正定拉普拉斯矩阵。使用L2范数的主要优点是优化问题有闭式解。然而,得到的系数向量是稠密的,因此affinity矩阵包含来自不同子空间的点之间的连接。最杰出的基于谱的子空间聚类算法当属稀疏子空间聚类(SSC)。在其最通用的公式中,SSC考虑了来自每个子空间的点同时受到噪声和稀疏外围输入污染的可能性。在SSC中,以下问题的形式为:

因此,SSC将近似误差分解为两个分量( η i \textbf η_i ηi和 z i z_i zi),这两个分量用不同的norm进行度量。继SSC的成功之后,提出了几种变体,包括具有正交匹配追踪的SSC(SSC-OMP)、结构化稀疏子空间聚类(S3C)和仿射稀疏子空间聚类(ASSC(Li等人,2018)。
与我们的方法最密切相关的方法是稀疏单纯形表示(SSR)算法,由Huang等人于2013年提出,用于脑网络建模。SSR使用p=L2和q=L1解决了(3)中的问题,附加约束是系数向量必须位于N−1维的单位形中: β i ∈ ∆ N − 1 = { β ∈ R N − 1 ∣ β > 0 , β ⊤ 1 = 1 \textbf β_i∈ ∆^{N−1} =\{\textbf β∈\mathbb R^{N-1}|\textbf β>0,\textbf β^\top\textbf 1=\textbf 1 βi∈∆N−1={β∈RN−1∣β>0,β⊤1=1。由于SSR通过其他点的凸组合近似表示 x i x_i xi,因此系数具有概率解释。然而,SSR没有诱导正则化,因为对于所有 β i ∈ ∆ N − 1 \textbf β_i∈ ∆^{N−1} βi∈∆N−1都有 ∣ ∣ β ∣ ∣ 1 = 1 ||\textbf β||_1=1 ∣∣β∣∣1=1,因此系数向量是稠密的。
约束聚类和主动学习
接下来,我们将简要概述使用外部信息的聚类,称为约束聚类(Basu et al.,2008)和主动学习。由于篇幅的限制,我们只提到与我们的问题最密切相关的工作。在约束聚类中,外部信息可以是类标签的形式,也可以是成对的“必须链接”和“不能链接”约束。
用于约束聚类的谱方法通过修改affinity矩阵来合并这些信息。 约束谱分割(CSP)(Wang和Davidson,2010)引入了一个成对约束矩阵,并解决了一个改进的归一化谱聚类分割问题。分区级约束聚类(PLCC)(Liu等人,2018)通过边信息矩阵形成成对约束矩阵,边信息矩阵作为惩罚项包含在归一化的分割目标函数中。受限结构化稀疏子空间聚类(C-S3C)(Li等人,2017)是专门为子空间聚类而设计的。CS3C合并了一个边信息矩阵,该矩阵将成对约束编码到S3C的公式中,该算法交替求解系数矩阵和聚类标签。仅依赖于修改亲和矩阵的约束聚类算法不能保证满足所有约束,因此C-S3C+(Li等人,2018b)是C-S3C的一个扩展,它在谱聚类阶段应用约束 k k k-means算法以确保满足约束条件。
在主动学习中,算法控制获取外部信息的点的选择。大多数主动学习技术用于有监督学习,很少有研究考虑子空间聚类的主动学习问题。Lipor和Balzano(2015,2017)提出了两种主动学习策略:
- 第一种方法将重建误差最大的点查询到其分配的子空间。第二个查询与其最近的两个子空间最大等距的点。
- 谱聚类的第二种策略通过将“必须链接”和“不能链接”点对的affinity系数分别设置为1和0。
两种策略都能有效识别错误标记的点。然而,正确地分配这些点并不能保证最大限度地提高估计子空间的准确性,从而提高聚类的整体质量。Peng和Pavlidis(2019)提出了一种顺序查询点的主动学习策略,以最大限度地减少(2)中的整体重建误差。
3. 加权稀疏单纯形表示
在本节中,我们将介绍所提出的基于谱的子空间聚类方法,称为加权稀疏单纯形表示(WSSR)。在这里,我们描述了WSSR算法,假设没有可用的标记数据。下一节中描述的约束聚类版本适用于在学习过程开始时具有标记观测子集的情况。
d i j ≥ 0 d_{ij}\geq 0 dij≥0度量了 x i , x j ∈ X x_i,x_j\in \mathcal X xi,xj∈X之间的差异性, I \mathcal I I为 X / { i } \mathcal X/\{i\} X/{i}中与 x i \textbf x_i xi具有有限差异的所有点的index集,即: I = { 1 ≤ j ≤ N ∣ d i j < ∞ , j ≠ i } \mathcal I=\{1\leq j\leq N|d_{ij}<\infin,j\neq i\} I={1≤j≤N∣dij<∞,j=i}。在WSSR中,每个 x i \textbf x_i xi的系数向量是以下凸优化问题的解:
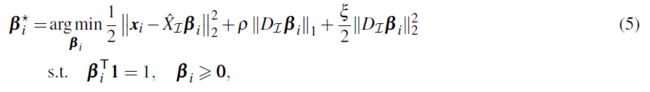
其中 X ^ I ∈ R P × ∣ I ∣ \hat X_\mathcal I\in \mathbb R^{P\times|I|} X^I∈RP×∣I∣是一个矩阵,其列为 X I X_\mathcal I XI中缩放后的点,而 D I D_\mathcal I DI为之前所提到的与 x i \textbf x_i xi具有有限差异性组成的对角阵。
我们首先概述我们选择罚函数的动机,然后在下一段讨论 X ^ I \hat X_\mathcal I X^I的定义和 d i j d_{ij} dij的选择。我们在(5)中使用L1和L2范数的动机是弹性网公式。L1范数诱导了得到差异点系数为零的解。L2范数惩罚鼓励所谓的分组效应。这对于子空间聚类是可取的,因为这样一个组中的点应该属于同一个子空间。在这种情况下,如果该子空间与 x i x_i xi所属的子空间不同,则应为所有点指定一个为零系数。相反,如果所有点来自与 x i x_i xi相同的子空间,则将 x i x_i xi连接到所有点是有益的,因为这增加了来自每个子空间的点属于由affinity矩阵 A A A定义的图的单个连接的概率。
谱子空间聚类算法通常在估计系数向量之前将 X X X中的点归一化为单位L2范数。图1中的简单示例说明了这种归一化倾向于增加聚类可分性。

在接下来,我们定义:
![]()
将数据投影到单位球面对WSSR问题有重要影响。在(5)中,我们希望最小化近似误差和选择几个相邻点这两个相互冲突的目标是分开的。图2的示例显示了,在投影到单位球体上之后的反例。
在图2中,单位球面上最接近 x ‾ i \overline x_i xi的点是 x ‾ 1 \overline x_1 x1。 x ‾ i \overline x_i xi的方向可以完全由 x ‾ 1 \overline x_1 x1和 x ‾ 2 \overline x_2 x2的凸组合逼近,但所有凸组合 α x ‾ 1 + ( 1 − α ) x ‾ 2 , α ∈ ( 0 , 1 ) \alpha\overline x_1+(1-\alpha)\overline x_2, \alpha \in (0,1) αx1+(1−α)x2,α∈(0,1)的L2范数小于1。由于 β i β_i βi的基影响近似的长度,因此它同时影响惩罚项和近似误差。
