机器学习第三章单变量线性回归（《大话Python机器学习》学习笔记）

3.1回归本质

3.1.1拟合概念

通过数据之间的关系建立一种近似的函数关系

3.1.2拟合与回归的区别

• 通过拟合方法可能找到关系曲线，但是不能确定对未知的数据拟合程度
• 寻找合适的曲线，越来越难
• 拟合是人们主观感知

3.1.3回归的诞生

《遗传的身高向平均数方向的回归》
Regression

3.1.4回归的本质含义

不仅是数据拟合手段，更是预测，不断向平均值回归

3.2单变量线性回归算法

用两个变量建立线性回归方程，来拟合与预测两变量关系的算法
常规求解：
  最小二乘法（实际值与预测值之间偏差的平方和最小来拟合曲线）
回归的评价方法：
  R方、均方误差（MSE）、均方根误差（RMSE）等

3.2.1单变量线性回归基本设定

单变量线性回归分析：
  在回归分析中，只包含一个自变量与一个因变量，且因变量自变量之间关系为线性关系。

• 前提：x与y最好有线性关系

多变量线性回归分析：
  回归分析种包含两个或两个以上的自变量，且因变量和自变量之间的关系为线性关系。

基本模型：
  h_θ(x)=θ₀+θ₁x

• h_θ(x)表示以θ为参数的学习算法解决方案或函数，是一个从x到y的函数映射
• θ₀和θ₁是回归参数、未知
• x为自变量，机器学习中也称特征变量、输入变量
• y为因变量，机器学习中也称目标变量、输出变量

注：

• 在统计学中，着重研究x与y的关联关系，因此称为自变量、因变量
• 在机器学习中，注重于研究x对y的预测，因此称为特征变量、目标变量

3.2.2单变量线性回归常规求解

常规方法：

• 最小二乘法

成本/代价/损失函数：

m	训练集中训练样本的个数
（x(i),y(i)）	第i个训练样本，上标i是索引，表示第i个训练样本

陈本函数最小问题的常规解法：

• 对成本函数求偏导，并令其等于0，所得到的θ即为模型参数的值

3.2.3单变量线性回归评价与预测

回归算法中，主要的评价方法：

• 平均绝对差值（MAE）
    mean absolute error：目标变量每个样本i的预测值与实际值差的绝对值，加总之后求平均：
• 图
• yf⁽ⁱ⁾为预测值
• 均方误差（MSE）
    mean square error：目标变量每个样本i的预测值与实际值差的平方，加总之后求平均：
• 图
• 均方根误差（RMSE）
    root mean square error：在均方误差MSE开根号：
• 图
• 拟合优度（R²）
    是判断回归模型拟合程度好坏的最常用的指标：
• 图
• 取值范围0-1，越接近1，拟合效果越好

除了对自身数据进行拟合与评价外，当模型训练完毕后，我们需要使用一个与训练数据集独立的新的数据集去对训练模型进行验证。
获取新的数据集：

1. 将已有的数据集随机分为两部分，一部分用来训练模型，一部分用来验证与评估模型
2. 重采样：对已有的数据集进行有放回地采样，然后将数据集随机划分成两部分，一部分训练，一部分验证评估

3.3用机器学习思维构建单变量线性回归模型

3.3.1波士顿房屋价格的拟合与预测

采用Scikit-learn的内置数据集波士顿房屋价格
采用单变量线性回归算法对数据进行拟合预测

特征变量	目标变量
房屋价格（MEDV）	每个房屋的房间数量（RM）

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.datasets import load_boston

# 导入数据
boston = load_boston()
print(boston.keys())
print(boston.feature_names)

bos = pd.DataFrame(boston.data)
print(bos[5].head())

bos_target = pd.DataFrame(boston.target)
print(bos_target.head())

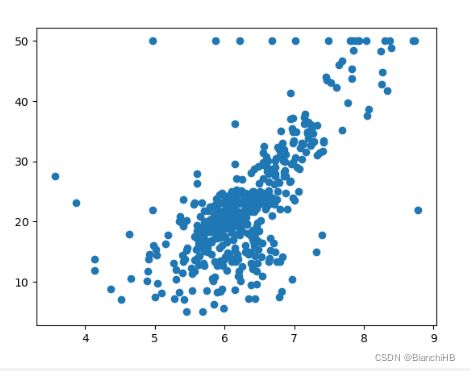
# 绘制散点图
x = bos.iloc[:,5:6]
y = bos_target
plt.scatter(x,y)
plt.show()

3.3.2数据集划分

在有监督的机器学习中，数据集被划分为：

训练集（课本）	用于训练的数据集，从而得到模型的未知参数
验证集（作业）	评估训练集的效果，调整参数，最好性能
测试集（考试）	测试训练后模型的子集，用来评价模型泛化能力

划分数据集：

• 数据量较大时，训练集占50%，验证集和测试集各占25%
• 数据量较小时，采用交叉验证，把初始数据集进行分组，一部分作为训练集训练模型，一部分作为验证集来评价模型。
    k折交叉验证：
      先将数据集D划分为k个大小相同的互斥子集，对于每个子集，尽可能保持数据分布的一致性（如正负比例在训练集和验证集中相同）；然后，每次用k-1个子集的并集作为训练集，剩下的一个子集作为验证集，这样就获得了k组训练/验证集，从而可以进行k次训练和验证，最终返回的是k个测试结果的均值。
    交叉验证法：将n次交叉验证的平均结果作为选择最合适的模型的依据。

# 导入数据
boston = load_boston()
bos = pd.DataFrame(boston.data)
bos_target = pd.DataFrame(boston.target)
# 数据转化
X = bos.iloc[:,5:6]
y = bos_target
X = np.array(X.values)
y = np.array(y.values)
# 数据划分
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.25)
print(X_train.shape,X_test.shape,y_train.shape,y_test.shape)

3.3.3模型求解与预测的Python实现

采用Scikit-learn库中的LinearRegression实现对线性回归的求解和预测

lr = LinearRegression()
# 求解参数
lr.fit(X_train,y_train)
print('a=',lr.coef_)
print('b=',lr.intercept_)
# 测试集进行预测
y_hat = lr.predict(X_test)
print(y_hat)

3.3.4模型评价

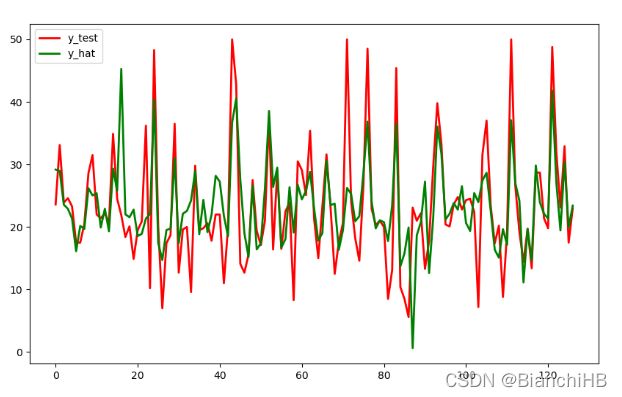
• 图形比对

plt.figure(figsize=(10,6))
t = np.arange(len(X_test))
plt.plot(t,y_test,'r',linewidth = 2,label = 'y_test')
plt.plot(t,y_hat,'g',linewidth = 2,label = 'y_hat')
plt.legend()
plt.show()

• R²、MAE、MSE、RMSE

r2_1 = lr.score(X_test,y_test)
r2_2  = r2_score(y_test,y_hat)
MAE = metrics.mean_absolute_error(y_test,y_hat)
MSE = metrics.mean_squared_error(y_test,y_hat)
RMSE = np.sqrt(metrics.mean_squared_error(y_test,y_hat))
print("r2={}\nr2={}\nMAE={}\nMSE={}\nRMSE={}\n".format(r2_1,r2_2,MAE,MSE,RMSE))

r2=0.516602648405293
r2=0.516602648405293
MAE=3.8799660045066524
MSE=38.24985587763383
RMSE=6.184646786812795

• 对于MAE、MSE、RMSE评估结果需要进行比较才有意义

3.3.5与最小二乘法预测效果比较

# 最小二乘法
def linefit(x,y):
    N = len(x)
    sx,sy,sxx,syy,sxy = 0,0,0,0,0
    for i in range(0,N):
        sx += x[i]
        sy += y[i]
        sxx += x[i] * x[i]
        syy += y[i] * y[i]
        sxy += x[i] * y[i]
    a = (sy * sx / N - sxy)/(sx * sx / N - sxx)
    b = (sy - a * sx)/N
    return a,b

a,b = linefit(X_train,y_train)
y_hat1 = a * X_test + b
MAE = metrics.mean_absolute_error(y_test,y_hat1)
MSE = metrics.mean_squared_error(y_test,y_hat1)
RMSE = np.sqrt(metrics.mean_squared_error(y_test,y_hat1))
print("MAE={}\nMSE={}\nRMSE={}\n".format(MAE,MSE,RMSE))

MAE=5.104824579532293
MSE=51.6002718147744
RMSE=7.183332918275082

3.4机器学习流程

1. 数据准备与需求分析
     包括所搜集的数据包含多少变量与样本，每个变量所代表的含义。特征变量和目标变量分别是那些。
2. 数据预处理
     导入数据、数据转化、数据可视化等。
3. 数据集划分
     划分为训练集、验证集、测试集。验证集并不是必须的。(train set,validation set,test set)
4. 算法的训练
     对模型参数的求解。
5. 算法的测试
     根据求得的参数，来对目标变量进行预测。
6. 算法的评估
     在有监督机器学习算法下，若预测数据的真实值已知，可以与预测值进行比较，得到MAE、MSE、RMSE等模型评价指标。