《速通机器学习》-第七章 集成学习

7.1　决策树

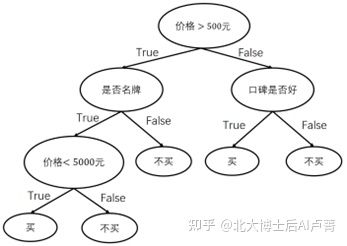
在现实生活中，我们每天都会面对各种抉择，例如根据商品的特征和价格决定是否购买。不同于逻辑回归把所有因素加权求和然后通过Sigmoid函数转换成概率进行决策，我们会依次判断各个特征是否满足预设条件，得到最终的决策结果。例如，在购物时，我们会依次判断价格、品牌、口碑等是否满足要求，从而决定是否购买。决策的流程，如图7-1所示。

图7-1

可以看到，决策过程组成了一棵树，这棵树就称为决策树。在决策树中，非叶子节点选择一个特征进行决策，这个特征称为决策点，叶子节点则表示最终的决策结果。在上例中，我们只是根据经验主观建立了一棵决策树，这棵决策树在数据量和特征维度较小且逻辑简单时是可以使用的。然而，在数据量和特征维度较大时，仅凭主观观察建立决策树显然是不可行的。在实际应用中，训练集中的样本往往有上万个，样本的特征通常有上百维，该怎么处理呢？在实际建立决策树的过程中，每次选择特征都有一套科学的方法。下面就详细讲解如何科学地建立决策树。

不难发现，建立决策树的关键在于选取决策点时使用的判断条件是否合理。每个决策点都要有区分类别的能力。例如，在电商场景中，将发货的快递公司作为决策点的选取条件就是一个很差的选择，其原因在于快递公司和购买行为没有必然联系，而将商品价格作为决策点的选取条件就是合理的，毕竟大部分消费者对商品价格比较敏感。

一个好的决策点可以把所有数据（例如商品）分为两部分（左子树和右子树），各部分数据所对应的类别应尽可能相同（例如购买或不购买），即两棵子树中的数据类别应尽可能“纯”（这种决策点有较高的区分度）。和逻辑回归类似，用已知数据（例如用户的购买记录、商品信息）求解决策树的形状和每个决策点使用的划分条件，就是决策树的训练过程。

首先看一下如何量化数据的纯度。假设在一组数据中有P和N两类样本，它们的数量分别为 n_1 个和 n_2 个。P类样本出现的概率为

P(y=P类)=n_1/(n_1+n_2 )

N类样本出现的概率为

P(y=N类)=n_2/(n_1+n_2 )

我们可以直观地发现：当数据只有一个类别（P(y=N类)=1 或 P(y=P类)=1）时，数据最纯；当两类数据“平分秋色”（P(y=N类)=P(y=P类)=0.5）时，数据最混乱。

可以使用基尼（Gini）系数来量化数据的混乱程度。基尼系数的计算公式如下。

Gini=1-〖P(y=N类)〗^2-〖P(y=P类)〗^2

可见，基尼系数越小，数据就越纯（P(y=N类)=1，Gini=0）。当数据最混乱时，P(y=N类)=P(y=P类)=0.5，也就是说，基尼系数的最大值为0.5。

基尼系数和概率 P(y=N类) 的关系，如图7-2所示。

图7-2

决策树有一些常用的构建方法，在这里我们详细讲解一下最为流行的CART树。CART树是一棵二叉树，它不仅能完成分类任务，还能完成数值预测类的回归任务。下面先介绍分类树，再介绍回归树。在构建CART树时，可以使用基尼系数来度量决策条件的合理性。

假设有 N 个训练样本，特征一共有 m 维，即 x=[■(x_1@⋮@x_m )]。和逻辑回归中特征 x_i 是连

续值不同，在这里，x_i 既可以是连续值（例如价格、好评数、销量等，x_i∈(-∞,+∞)），也可以从集合中“多选一”（例如学历，x_i∈{专科,本科,硕士,博士,其他}）。决策树的构建（训练）过程是一个不断生成决策点的过程，每次生成的决策点都要尽可能把训练样本中的两类数据分开。

例如，x_1 为价格，划分条件为 x_1>500，将训练数据分成两类（如果某个样本在划分条件上有特征缺失，就随机分配该样本），如图7-3所示。

图7-3

Data1 中有 M_1 个样本，它们对应于不同的类别，基尼系数为 Gini1。Data1 中的数据越纯（类别越单一），Gini1 就越小。同理，Data2 中有 M_2 个样本，基尼系数为 Gini2。

此次划分的基尼系数为

Gini(x_1>500)=M_1/(M_1+M_2 ) Gini1+M_2/(M_1+M_2 ) Gini2

Gini(x_1>500) 为 Gini1 和 Gini2 加权求和（权重为两堆数据的数量占比）的结果，用于度量划分条件 x_1>500 的合理性。Gini(x_1>500) 越小，说明度量划分越合理。

若 x_2∈{专科,本科,硕士,博士,其他}，则可将“x_2=本科”作为划分条件，将数据划分为“x_2=本科”“x_2≠本科”两部分，并计算基尼系数 Gini(x_2=本科)。

遍历所有维度（i=1,2,3,⋯,m）中可能的划分条件，对每种划分方法均可计算相应的基尼系数，例如 Gini(x_1>500)、Gini(x_1>600)、Gini(x_1>400)、Gini(x_2=本科)、Gini(x_2=博士)、Gini(x_3>5)。以最小基尼系数所对应的特征和划分条件为决策点，数据将被划分为两堆。但是，决策树是不停生长的，仅划分一次是不够的，需要再使用同样的方法对每个子堆（Data 1、Data 2）进行划分，最终生成CART树，步骤如下。算法的输入为训练集 D、基尼系数的阈值、样本数量的阈值，输出为决策树 T。算法从根节点开始，用训练集递归建立CART树。

 当前节点的数据集为 D。如果样本数量小于阈值、基尼系数小于阈值或没有特征，则返回决策子树，当前节点停止递归。

 在当前节点的数据上计算各个特征的各个划分条件对划分后的数据的基尼系数。当维度过高且每维所对应的可取值比较多时（例如，价格的值为 1~10000 的整数，将有10000种划分方式；如果为浮点数，划分方式更多），可以随机选取一些特征和划分条件，不再强制要求全部遍历。

 在计算出来的各个特征的各个特征值对数据集 D 的基尼系数中，选择基尼系数最小的特征 x_i 和对应的划分条件，例如“x_i>10”或“x_i=本科”。通过划分条件把数据集划分成 Data1 和 Data2 两部分，同时分别建立当前节点的左节点和右节点，左节点的数据集为 Data1，右节点的数据集为 Data2。

 对 Data1 和 Data2 递归调用以上步骤，生成决策树。

这就是决策树的训练过程。在第步中，判断样本数量和基尼系数是为了控制生成的决策树的深度，避免不停地递归。不停地递归会导致划分条件过细，从而造成过拟合。

决策树建立后，每个叶子节点里都有一堆数据。可以将这堆数据的类别比例作为叶子节点的输出。

决策树在复杂度上和其他模型有所不同。例如，在逻辑回归中，当特征维度不变时，模型的复杂度就确定了。但是，在决策树中，模型会根据训练数据不断分裂，决策树越深，模型就越复杂。可以看出，数据决定了决策树的复杂度，且当数据本身线性不可分时，决策树会非常深，模型会非常复杂。所以，在决策树中，需要设置终止条件，以防模型被数据带到极端复杂的情况中。在决策树中，终止条件的严格程度相当于逻辑回归中正则项的强度。

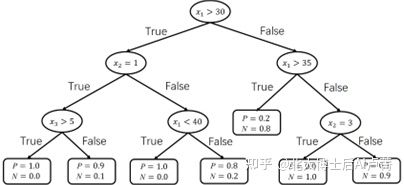
训练完成后，我们可以得到一棵决策树，如图7-4所示。

在使用决策树时，用数据 x 在决策树上找到对应的叶子节点作为分类结果。例如，当

x=[■(35@1@2)] 时，对应的分类结果为 P(P类)=0.9，P(N类)=0.1。决策树对输入 x 的预测结

果常写为 h(x)，h 表示决策树的决策过程。

决策树理解起来比较简单，其本质就是以基尼系数来量化划分条件的分类效果，自动探寻最佳划分条件。

图7-4

下面我们把决策树和逻辑回归进行对比。为了方便对比，假设决策树的特征为2维且均为连续特征。决策树的分类效果图可以理解为如图7-5所示的形式。

图7-5

可见，决策树分类的几何意义和逻辑回归一样，都是在平面上画直线。相比逻辑回归的分类线是一条直线，决策树的分类线是平面上与坐标轴平行的多条直线（一个判断条件对应于一条直线，这些直线共同组成了分类线）。多条直线可以组合成非线性的形式，以处理线性不可分的情况，如图7-6所示。

虽然决策树在训练时需要遍历所有可能的类别划分方法，速度比较慢，但是在预测阶段，决策树只需进行一些逻辑判断和比较，速度非常快，故适合在对时间要求较高的场景中使用。

决策树不仅可以用在分类中，还可以用在回归中（预测连续的值而非类别概率）。用在分类中的决策树称为分类树，用在回归的中决策树称为回归树。在回归任务中，学习目标不再是分类，而是一个连续值 y_i∈(-∞,+∞)。此时，基尼系数不再适用于衡量数据的混乱程度，一般使用方差来衡量数据的混乱程度。

图7-6

例如，当 x_1>20 时，将它作为划分条件，把数据划分为 Data1 和 Data2 两部分，Data1中有 M_1 个样本，Data2 中有 M_2 个样本。

Data1 中数据的混乱程度为

σ_1^2=∑_(i∈Data1)▒〖〖(y〗_((i))-μ_1)〗^2

μ_1 为 Data1 中目标值的平均值，即

μ_1=1/M_1 ∑_(i∈Data1)▒y_((i))

如果 Data1 中所有数据的目标值 y_((i)) 都一样，那么 σ_1=0，此时 Data1 中的数据最纯。

同理，可以求出 Data1 中数据的混乱程度 σ_2^2。

对于划分条件 x_1>20，其对应的混乱程度为

σ(x_1>20)=σ_1^2+σ_2^2

回归树除了使用方差代替基尼系数来度量数据的纯度，其他均与分类树一致，叶子节点输出的值为该节点所有样本目标值的平均值。

7.2　随机森林

通过前面的学习不难发现，CART树是一个强分类器。理论上，它可以对任意数据分布进行分类（不停地划分，直至叶子节点中只有一类数据）。这种强分类器在训练集上能得到非常好的效果。

然而，令人遗憾的是，在测试集（真实场景）中，决策树非常容易发生过拟合，其原因之一就是规则太“硬”。例如，以“年龄>25岁”为条件进行划分，那么26岁和24岁所对应的类别有本质区别吗？当然没有。可见，决策树把特征绝对化了。另外，如果训练样本中有一些极端样本，例如一位75岁的老人购买了一台游戏机，那么，用决策树进行学习，就会得到“年龄>75岁会购买游戏机”的分类结果，而这种异常结果并不是我们想要的。

决策树过于在意降低经验风险，其代价是结构风险较高（决策树不停生长，模型的复杂度越来越高），这也是和奥卡姆剃刀定律相悖的。通过上述分析可以发现，决策树的泛化能力不好，容易学到一些极端特例，非常容易出现过拟合。

综上所述，决策树出现过拟合的原因在于，模型不仅容易对个别特征及其取值过于敏感，还容易被个别样本影响。

为了消除这些问题，我们可以选取部分特征及部分数据来构建决策树，从而在大概率上忽略极端数据。这是一个双重随机过程，具体如下。

第一次随机：设全量样本数为 N，有放回地随机抽取 M 条数据作为训练样本。

第二次随机：在抽取的 M 条数据中，从所有特征 x=[x_1,x_2,⋯,x_m ]^T 中随机选取特征（例如 x_1、x_3、x_5），忽略其他特征。

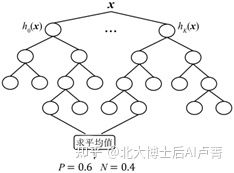
通过双重随机选取训练样本和特征，可以构建决策树 h_1。重复这个双重随机过程，构建决策树 h_2,h_2,h_3,⋯,h_K。这 K 棵决策树组成一个森林，称为随机森林（Random Forest）。因为在构建这 K 棵决策树时使用的特征和样本不是完全相同的，所以，不同的决策树的形状

可能不同。将这 K 棵决策树的分类结果的平均值作为最终结果，即 y^'=1/K ∑_(i=1)^K▒〖h_i (x)〗。

随机森林的分类流程，如图7-7所示。

图7-7

随机森林的分类线，如图7-8所示。

图7-8

例如，当 K=3 时，分类结果如表7-1所示。随机森林预测为P类的概率为0.6，预测为N类的概率为0.4。

表7-1

在随机森林中，每棵决策树都是一个强分类器。强分类器在训练集上的分类效果很好，但会带来过拟合问题，而过拟合问题产生的原因就是分类器学会了数据中的随机噪声。分类器在有噪声的数据中学习，等价于给各个分类器注入了噪声。因为随机森林的预测结果是多棵决策树投票决定的，而单棵决策树由于数据噪声出现导致的分类错误会通过求平均值的计算得以消除，所以，随机森林的表现一般要优于单棵决策树。

例如，有 n 个符合正态分布的噪声

Noise_i~N(0,σ^2)

噪声的平均值为0，方差为 σ^2。σ^2 越大，说明噪声的负面影响越大。如果 K 棵决策树的输入数据相互独立（Noise_i~Noise_K 相互独立），就可以对噪声进行平均，得到

Noise=1/K ∑_(i=1)^K▒Noise_i ~N(0,σ^2/K)

从上式中可以看出，通过对 K 棵决策树各自的独立噪声进行平均，方差可降至原来的 1/K，噪声的影响将按比例缩小。因此，对多分类器求平均值可以起到降低噪声、提高泛化能力的作用，这就是随机森林的理论基础。

如果噪声来源完全一致，则 Noise~N(0,σ^2)，而噪声的方差不会减小。因此，我们希望各决策树相互独立。双重随机过程会尽可能使各决策树在训练时使用的样本相互独立，从而使各决策树相互独立。

要想最大限度发挥随机森林的作用，就要使各决策树相互独立，即所用特征和训练样本都是独立抽取的。做一个极端的假设：如果不使用双重随机方法去训练 K 棵决策树，那么这 K 棵决策树的训练只是简单的复制，错误会同时出现在所有决策树中，问题仍然得不到解决。随机森林的运作模式其实就是“三个臭皮匠，顶个诸葛亮”，即要求“三个臭皮匠”的能力尽可能互补，而不是整齐划一。

将一棵决策树当作一位精通某个较小领域的专家（因为每棵决策树使用的特征不同），这样在随机森林中就有了多位精通不同的较小领域的专家。这样，我们就可以从不同的角度看待一个新问题（新的输入数据），最终通过这些“专家”的“投票”得到结果了。

7.3　GBDT

在二分类决策树中，将特征输入决策树，会得到分类结果

y^'=h(x)

h(x) 决定了特征 x 将落入哪个叶子节点，并给出了对应的输出（值域为 [0,1]）。叶子节点的输出只能是 [0,1]，这是一个强限制。多个分类器的集成（随机森林）只能通过求平均值的方式进行，以保证最终结果的值域为 [0,1]。

参考逻辑回归，可以对叶子节点进行改造，将 h(x) 的值域扩大至 (-∞,+∞)，然后通过Sigmoid函数将其转换成概率，公式如下。

y^'=1/(1+e^(-h(x)) )

此时，决策树已经不是分类树了，而是回归树，可以通过Sigmoid函数将决策结果 h(x) 转换成概率 y^'（可以类比线性回归和逻辑回归之间的关系）。在分类场景中，可以将多棵回归树集成。尽管回归树不会直接给出分类结果，但每棵回归树的叶子节点都有相应的得分 h(x)，通过逻辑回归即可将得分转换成概率。

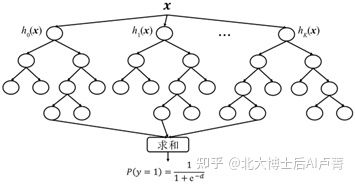
这种方法的好处在于所有决策树都不再受值域的限制，输出更加灵活。类比随机森林，若通过将 K 棵决策树进行集成来完成预测任务，则

y^'=1/(1+e^(-∑_(m=0)^K▒〖h_m (x)〗) )

这就是梯度升级决策树（Gradient Boosting Decision Tree，GBDT）。

同样是多棵决策树集成，GBDT和随机森林的主要区别如下。

在随机森林中，每棵决策树都能独立给出分类结果的概率。对这些概率求平均值，就能得到最终的分类结果。

在GBDT中，每棵决策树只提供一个得分，其集成结果就是将得分相加，然后使用Sigmoid函数将得分转换成概率。

这样做有什么好处呢？GBDT可以使每棵决策树的训练目标不再是最终分类结果，而是前面 k 棵决策树的结果和最终目标的差异（Gap）。这也决定了训练GBDT中的决策树需要

采用串行方法：训练前 k 棵决策树，计算前 k 棵决策树的分类结果 y^'=1/(1+e^(-∑_(m=0)^k▒〖h_m (X)〗) ) 和真

实目标 y 之间的误差；在训练第 k+1 棵决策树时，目标就是这个误差，而不是最终的分类结果。类比复习备考的过程，随机森林就是在每次考试前把所有习题都做一遍，而GBDT只关注在上一次考试中做错的题。

下面具体分析GBDT的学习过程。

假设已经完成前 k 棵决策树的学习（前 k 棵决策树是已知的），那么当前的学习器为

F_k (x)=∑_(m=0)^k▒〖h_m (x)〗

也就是说，对于训练样本 {x_((i)),y_((i))}，预测结果为

y_((i))^'=1/(1+e^(-∑_(m=0)^k▒〖h_m (x_((i)))〗) )=1/(1+e^(-F_k (x) ) )

仍然用KL距离来度量 y_((i))^' 和目标 y_((i)) 之间的差异，有

Loss_((i))=-y_((i) ) logy_((i))^'-(1-y_((i) ) )log(1-y_((i))^')

在GBDT中，添加 h_(k+1) (x) 的目标是减小 Loss_((i))，那么 h_(k+1) (x) 取多少才合适呢？添加

h_(k+1) (x)，学习器 F_k (x) 将变为 F_(k+1) (x)，即 F_(k+1) (x)=F_k (x)+h_(k+1) (x)，最终导致分类结

果 y_((i))^' 发生变化。通过对梯度下降法的分析可以知道，为了使 Loss_((i)) 变小，F_(k+1) (x) 应朝着

-(∂Loss_((i)))/(∂F_k (x_((i)) ) ) 的方向变化，即 h_(k+1) (x_((i))) 的学习目标的方向为 r_((i),k+1)=-(∂Loss_((i)))/(∂F_k (x_((i)) ) )，公式如下。

r_((i),k+1)=-(∂Loss_((i)))/(∂F_k (x_((i)) ) )=y_((i) )-y_((i))^'=y_((i) )-1/(1+e^(-F_k (x_((i)) ) ) )

在训练回归树 t_(k+1) (x) 时，使用的训练样本为

〖〖{x〗_((i)),r_((i),k+1)}〗_(i=1)^N

在这里，训练的回归树是 t_(k+1) (x)，而不是 h_(k+1) (x)，其主要原因是：r_((i),k+1) 是下一棵决策

树的目标方向，而不是真实值（类比逻辑回归，需要给梯度乘以学习因子来修正）。所以，t_(k+1) (x) 只能提供正确的决策点（树结构）。但是，叶子节点的输出值需要修正。若 t_(k+1) (x) 有 j=1,2,⋯,J_(k+1) 个叶子节点，则每个叶子节点的输出值可以修正为

c_(k+1,j)=(∑_(x_((i))∈R_(k+1,j))▒r_((i),k+1) )/(∑_(x_((i))∈R_(k+1,j))▒〖〖(y〗_((i))-r_((i),k+1))〖(1-y〗_((i) )+r_((i),k+1))〗)

R_(k+1,j) 为训练样本中被 t_(k+1) (x) 划分至叶子节点 j 的数据的集合。

因此，t_(k+1) (x) 被修正（只修正叶子节点的输出值，不改变树结构）后就成为待求的决策树 h_(k+1) (x)，公式如下。

h_(k+1) (x)=∑_(j=1)^(J_(k+1))▒〖c_(k+1,j) I(x∈R_(k+1,j) ) 〗

I(x∈R_(k+1,j) )={█(1,如果 x∈R_(k+1,j)@0,如果 x∉R_(k+1,j) )┤

因为 x 最终会被划分至一个叶子节点，所以 I(x∈R_(k+1,j) ),j=1,⋯,J_(k+1) 有且仅有一

个为1。此时，学习器更新为

F_(k+1) (x)=F_k (x)+h_(k+1) (x)=∑_(m=0)^(k+1)▒〖h_m (x)〗

依此类推，可以学习 h_(k+2) (x),⋯,h_K (x)。

上述过程就是递归训练 h_k (x)。作为递归的开始，可直接令 h_0 (x)=log P/(1-P)，P 表示类别为 y=1 的样本在所有样本中的占比。

综上所述，如果有 N 个训练样本，则整个训练过程如下。

 初始化 h_0 (x)=log P/(1-P)。

 依次训练 h_1,⋯,h_K，共 K 棵决策树。

GBDT的分类流程图，如图7-9所示。不同于随机森林对所有决策树的结果求平均值，GBDT对所有决策树的结果求和，然后通过Sigmoid函数将其转换成分类结果。

图7-9

GBDT是一个非常实用的分类模型。尽管GBDT和随机森林都能对多棵决策树进行集成，但GBDT中的每棵决策树都“站在前人的肩膀上”，相比随机森林的每棵决策树都从零开始更具优势。如果说随机森林多棵决策树集成的目的是防止过拟合，那么GBDT的多棵决策树集成主要用于解决欠拟合问题。在训练时，不同于随机森林，GBDT的各个基学习器 h_k 存在强关联，无法进行并行训练。

在广告、推荐、搜索等领域，点击率在过去很长的时间里是通过逻辑回归模型进行预测的。但是，逻辑回归涉及大量的特征组合，这会消耗大量的人力和算力，依赖大量相关的业务经验。为了解决这些问题，Facebook提出了一种新型算法，先使用GBDT提取数据特征，再使用逻辑回归在提取的特征上进行预测。

一个GBDT模型架构，如图7-10所示。

图7-10

将特征 x 输入GBDT。在这个GBDT中，有3棵决策树，共7个叶子节点，提取后的特征有7维。特征 x 在第一棵决策树中落入第二个叶子节点，在第二棵决策树中落入第一个叶子节点，在第三棵决策树中落入第二个叶子节点，提取的特征为 〖[0,1,0,1,0,0,1]〗^T。将这个特征输入逻辑回归模型，即可完成预测。

这种先用GBDT提取非线性组合特征，再用线性模型（逻辑回归）进行分类的算法，实现了两种模型优势互补。