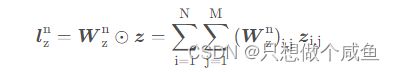PNN(Product-based Neural Network):模型学习及torch复现
一、前言
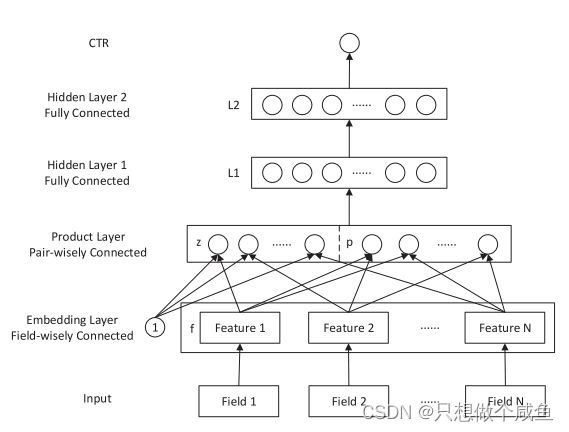
PNN模型在输入、Embedding层, 多层神经网络及最后的输出层与DeepCrossing没有区别, 唯一的就是Stacking层换成了Product层。 DeepCrossing把所有特征进行了交叉, 没有针对性, 所以PNN这里就弄了个Product层, 专门进行特征之间的交叉的, 并且还提出了两种特征交叉的方式。
二、PNN模型
PNN结构如下:
1、输入层
模型输入由N 个特征域(Field)组成,都是离散稀疏的分类特征,如年龄、性别、id等,数值型特征需要等类别型特征交叉完了之后, 再统一合并
2、Embedding层
对每一个离散稀疏的Field特征域进行Embedding操作,参数是通过神经网络的反向传播进行学习。 对于i 的每一个特征值, 都是一个1 × M的向量, 这里的M表示隐向量的维度。
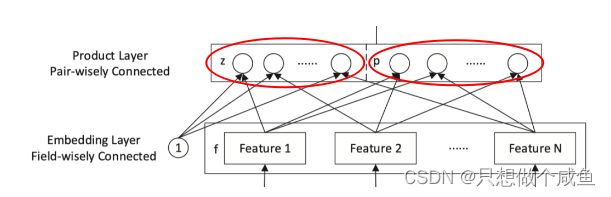
3、Product层
(1)左侧z
公式如下:
所有特征域的embedding组成的矩阵点乘一个权重矩阵![]() ,然后再求和得到的。
,然后再求和得到的。
N个特征域的embedding堆叠就会形成一个N × M的矩阵
(2)右侧p
公式如下:
上面的z 虑的是单个特征, 这时候每个域的embedding值乘1就完事了。 而这p考虑的是两两特征的交互
product层比一下和Stacking层的区别, 这里在保持了原来特征embedding的基础上, 特别研究了下embedding的两两交叉来增强模型的表达能力。
4、L1层
这个就是一个普通的那种全连接层了, 但是这里依然会有一个细节, 也就是product层的输出是![]() 和
和![]() ,仅代表了离散型的特征,数值型特征就是在这个时候加入进来了
,仅代表了离散型的特征,数值型特征就是在这个时候加入进来了
5、L2层
全连接层了
6、输出层
由于这个是二分类预测问题, 最后sigmoid进行激活输出,损失函数用的交叉熵损失函数
三、PNN模型pytorch复现
1、DNN层
class DNN(nn.Module):
def __init__(self, hidden_units, dropout=0.):
"""
hidden_units:列表, 每个元素表示每一层的神经单元个数,比如[256, 128, 64],两层网络, 第一层神经单元128个,第二层64,注意第一个是输入维度
dropout: 失活率
"""
super(DNN, self).__init__()
# 下面创建深层网络的代码 由于Pytorch的nn.Linear需要的输入是(输入特征数量, 输出特征数量)格式, 所以我们传入hidden_units,
# 必须产生元素对的形式才能定义具体的线性层, 且Pytorch中线性层只有线性层, 不带激活函数。 这个要与tf里面的Dense区分开。
self.dnn_network = nn.ModuleList(
[nn.Linear(layer[0], layer[1]) for layer in list(zip(hidden_units[:-1], hidden_units[1:]))])
self.dropout = nn.Dropout(p=dropout)
# 前向传播中, 需要遍历dnn_network, 不要忘了加激活函数
def forward(self, x):
for linear in self.dnn_network:
x = linear(x)
x = F.relu(x)
x = self.dropout(x)
return x用如下参数试一下DNN网络
hidden_units = [16, 8, 4, 2, 1] # 层数和每一层神经单元个数, 由我们自己定义了
dnn = DNN(hidden_units)
summary(dnn, input_shape=(16,))网络结构:
2、ProductLayers
class ProductLayer(nn.Module):
def __init__(self, mode, embed_dim, field_num, hidden_units):
super(ProductLayer, self).__init__()
self.mode = mode
# product层, 由于交叉这里分为两部分, 一部分是单独的特征运算, 也就是上面结构的z部分, 一个是两两交叉, p部分, 而p部分还分为了内积交叉和外积交叉
# 所以, 这里需要自己定义参数张量进行计算
# z部分的w, 这里的神经单元个数是hidden_units[0], 上面我们说过, 全连接层的第一层神经单元个数是hidden_units[1], 而0层是输入层的神经
# 单元个数, 正好是product层的输出层 关于维度, 这个可以看在博客中的分析
self.w_z = nn.Parameter(torch.rand([field_num, embed_dim, hidden_units[0]]))
# p部分, 分内积和外积两种操作
if mode == 'in':
self.w_p = nn.Parameter(torch.rand([field_num, field_num, hidden_units[0]]))
else:
self.w_p = nn.Parameter(torch.rand([embed_dim, embed_dim, hidden_units[0]]))
self.l_b = torch.rand([hidden_units[0], ], requires_grad=True)
def forward(self, z, sparse_embeds):
# lz部分
l_z = torch.mm(z.reshape(z.shape[0], -1), self.w_z.permute((2, 0, 1)).reshape(self.w_z.shape[2], -1).T)# (None, hidden_units[0])
# lp 部分
if self.mode == 'in': # in模式 内积操作 p就是两两embedding先内积得到的[field_dim, field_dim]的矩阵
p = torch.matmul(sparse_embeds, sparse_embeds.permute((0, 2, 1))) # [None, field_num, field_num]
else: # 外积模式 这里的p矩阵是两两embedding先外积得到n*n个[embed_dim, embed_dim]的矩阵, 然后对应位置求和得到最终的1个[embed_dim, embed_dim]的矩阵
# 所以这里实现的时候, 可以先把sparse_embeds矩阵在field_num方向上先求和, 然后再外积
f_sum = torch.unsqueeze(torch.sum(sparse_embeds, dim=1), dim=1) # [None, 1, embed_dim]
p = torch.matmul(f_sum.permute((0, 2,1)), f_sum) # [None, embed_dim, embed_dim]
l_p = torch.mm(p.reshape(p.shape[0], -1), self.w_p.permute((2, 0, 1)).reshape(self.w_p.shape[2], -1).T) # [None, hidden_units[0]]
output = l_p + l_z + self.l_b
return output3、PNN
# 下面我们定义真正的PNN网络
# 这里的逻辑是底层输入(类别型特征) -> embedding层 -> product 层 -> DNN -> 输出
class PNN(nn.Module):
def __init__(self, feature_info, hidden_units, mode='in', dnn_dropout=0., embed_dim=10, outdim=1):
"""
DeepCrossing:
feature_info: 特征信息(数值特征, 类别特征, 类别特征embedding映射)
hidden_units: 列表, 全连接层的每一层神经单元个数, 这里注意一下, 第一层神经单元个数实际上是hidden_units[1], 因为hidden_units[0]是输入层
dropout: Dropout层的失活比例
embed_dim: embedding的维度m
outdim: 网络的输出维度
"""
super(PNN, self).__init__()
self.dense_feas, self.sparse_feas, self.sparse_feas_map = feature_info
self.field_num = len(self.sparse_feas)
self.dense_num = len(self.dense_feas)
self.mode = mode
self.embed_dim = embed_dim
# embedding层, 这里需要一个列表的形式, 因为每个类别特征都需要embedding
self.embed_layers = nn.ModuleDict({
'embed_' + str(key): nn.Embedding(num_embeddings=val, embedding_dim=self.embed_dim)
for key, val in self.sparse_feas_map.items()
})
# Product层
self.product = ProductLayer(mode, embed_dim, self.field_num, hidden_units)
# dnn 层
hidden_units[0] += self.dense_num
self.dnn_network = DNN(hidden_units, dnn_dropout)
self.dense_final = nn.Linear(hidden_units[-1], 1)
def forward(self, x):
dense_inputs, sparse_inputs = x[:, :13], x[:, 13:] # 数值型和类别型数据分开
sparse_inputs = sparse_inputs.long() # 需要转成长张量, 这个是embedding的输入要求格式
sparse_embeds = [self.embed_layers['embed_'+key](sparse_inputs[:, i]) for key, i in zip(self.sparse_feas_map.keys(), range(sparse_inputs.shape[1]))]
# 上面这个sparse_embeds的维度是 [field_num, None, embed_dim]
sparse_embeds = torch.stack(sparse_embeds)
sparse_embeds = sparse_embeds.permute((1, 0, 2)) # [None, field_num, embed_dim] 注意此时空间不连续, 下面改变形状不能用view,用reshape
z = sparse_embeds
# product layer
sparse_inputs = self.product(z, sparse_embeds)
# 把上面的连起来, 注意此时要加上数值特征
l1 = F.relu(torch.cat([sparse_inputs, dense_inputs], axis=-1))
# dnn_network
dnn_x = self.dnn_network(l1)
outputs = F.sigmoid(self.dense_final(dnn_x))
return outputs 模型结构
总结
PNN, 强调了Embedding向量之间的交叉方式是多样化的, 相比于简单的交由全连接层无差别化的处理, PNN模型定义的内积和外积操作显然更有针对性的强调了不同特征之间的交互, 从而让模型更容易捕获特征的交叉信息。 But, PNN模型同样存在着局限, 比如外积操作在实际应用中, 为了优化训练效率进行大量的简化。 此外, 对所有特征无差别的交叉, 在一定程度上忽略了原始特征向量中包含的有价值信息。