NNDL 实验3 线性回归

目录

2.2 线性回归

2.2.1 数据集构建

2.2.2 模型构建

2.2.3 损失函数

2.2.4 模型优化

2.2.5 模型训练

2.2.6 模型评估

2.2.7 样本数量 & 正则化系数

2.3 多项式回归

2.3.1 数据集构建.

2.3.2 模型构建

2.3.3 模型训练

2.3.4 模型评估

2.4 Runner类介绍

2.5 基于线性回归的波士顿房价预测

2.5.1 数据处理

    2.5.1.2 数据清洗

    2.5.1.3 数据集划分

    2.5.1.4 特征工程

2.5.2 模型构建

2.5.3 完善Runner类

2.5.4 模型训练

2.5.5 模型测试

2.5.6 模型预测

---

2.2 线性回归

2.2.1 数据集构建

构造一个小的回归数据集：

生成 150 个带噪音的样本，其中 100 个训练样本，50 个测试样本，并打印出训练数据的可视化分布。

import torch
from matplotlib import pyplot as plt
def synthetic_data(w, b, num_examples):  # @save
    """生成y=Xw+b+噪声"""
    # torch.normal(mean,std,(m,n)) 取一标准差为mean，方差为std的正态分布中[m,n]大小的矩阵
    # torch.matmul(x,y)  表示矩阵x和y相乘
    X = torch.normal(0, 1, (num_examples, len(w)))  # 从一个标准正态分布中提取（num_examples，len（w）)大小的矩阵
    y = torch.matmul(X, w) + b  # 将矩阵X和w相乘并加上常量b，生成数据集的y
    y += torch.normal(0, 0.3, y.shape)  # 生成一个和y大小相同的高斯分布噪声加到y上
    return X, y.reshape((-1, 1))  # 返回x，y矩阵，并将y矩阵由行矩阵转换为列矩阵


true_w = torch.tensor([1.2])  # 设置进行线性变换的参数w
true_b = 0.5  # 设置线性变换的b
train_features, train_labels = synthetic_data(true_w, true_b, 100)  # 生成100个训练样本
test_features, test_labels = synthetic_data(true_w, true_b, 50)  # 生成50个测试样本
# 生成直线
start_train = min(train_features)  # 找到训练集数据中最小的那个数据并存入张量中
end_train = max(train_features)  # 找到训练数据集中最大的那个数据并存入张量中
# torch.linspace返回一个以start到end等距的steps的张量
line_x = torch.linspace(start_train[0], end_train[0], 50)  # 返回一个以start到end等距的50个数据的一维张量
line_y = torch.matmul(line_x.reshape((-1, 1)), true_w) + true_b  # 将矩阵line_x和矩阵line_y相乘并加上常量true_b
# 绘图
# plt.scatter(x,y,s,c,marker,label)x,y表示数据位置，s表示图形大小，c表示颜色，marker表示图形形状默认为圆点，label表示标签标题
plt.scatter(train_features, train_labels, s=10,  label='train data')  # 绘制训练集的散点图
plt.scatter(test_features, test_labels, s=10, c='red', label='test data')  # 绘制测试集的散点图
plt.plot(line_x, line_y, c='black', label='y=1.2*x+0.5')  # 将训练集和数据集绘图
plt.legend()  # 为图形添加图例
plt.show()  # 将图形展示出来

运行结果：

2.2.2 模型构建

在线性回归中，自变量为样本的特征向量x∈RD\boldsymbol{x}\in \mathbb{R}^Dx∈RD(每一维对应一个自变量)，因变量是连续值的标签y∈Ry\in Ry∈R。

线性模型定义为：

其中权重向量w∈RD\boldsymbol{w}\in \mathbb{R}^Dw∈RD和偏置b∈Rb\in \mathbb{R}b∈R都是可学习的参数。

#初始化模型参数
w = torch.normal(0, 0.01, size=(1,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
#模型构建
def linear_func(X, w, b):  #建立线性模型
    """线性回归模型"""
    return torch.matmul(X, w) + b

2.2.3 损失函数

回归任务是对连续值的预测，希望模型能根据数据的特征输出一个连续值作为预测值。因此回归任务中常用的评估指标是均方误差。

均方误差的定义为：

#损失函数
#y_hat代表预测值，y代表真实值
def squared_loss(y_hat, y):   #定义损失函数
    """均方损失"""
    return (y_hat - y.reshape(y_hat.shape)) ** 2

思考：没有除2合理么？ 

合理，因为我们计算时需要对损失函数求导，除2是为了求导后计算简单，是否除2对结果影响不大

2.2.4 模型优化

其中L2正则化是为了防止过拟合

#模型优化
#lr表示学习速率，
def sgd(params, lr, batch_size):  #定义模型优化函数
    """小批量随机梯度下降"""
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()

思考1. 为什么省略了1/N不影响效果？

 1/N是一个常数， 在反向传播求偏导时 ，对于相同的超参数只会影响收敛速度，并不会最终收敛的结果，在求导是就变为了一个常数。

 思考 2.  什么是最小二乘法

 最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合

2.2.5 模型训练

在准备了数据、模型、损失函数和参数学习的实现之后，我们开始模型的训练。在回归任务中，模型的评价指标和损失函数一致，都为均方误差。

通过上文实现的线性回归类来拟合训练数据，并输出模型在训练集上的损失。

# 模型训练
lr = 0.03
num_epochs = 6
net = linear_func
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, train_features, train_labels):
        l = loss(train_features * w + b, train_labels)  # X和y的小批量损失
        # 因为l形状是(batch_size,1)，而不是一个标量。l中的所有元素被加到一起，
        # 并以此计算关于[w,b]的梯度
        l.sum().backward()
        sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数
    with torch.no_grad():
        train_l = loss(net(train_features, w, b), train_labels)
        print(f'轮数： {epoch + 1}, loss {float(train_l.mean()):f}')
print(w, b)

运行结果：

2.2.6 模型评估

 用训练好的模型预测一下测试集的标签，并计算在测试集上的损失

y_predict = linear_func(test_features, w, b)
loss_test = squared_loss(y_predict, test_labels)
loss = 0
for i in loss_test:
    loss += i
print(loss/50)

 运行结果：

2.2.7 样本数量 & 正则化系数

（1）调整训练数据的样本数量，由 100 调整到 5000，观察对模型性能的影响。

w_pred tensor([[1.1998]], requires_grad=True)
b_pred tensor([0.4998], requires_grad=True)
loss 0.000080

（2）调整正则化系数，观察对模型性能的影响。

optimizer = torch.optim.SGD(model.parameters(),0.01,weight_decay=0.1)

2.3 多项式回归

2.3.1 数据集构建.

构建训练和测试数据，其中：

训练数样本 15 个，测试样本 10 个，高斯噪声标准差为 0.1，自变量范围为 (0,1)。

import math
import torch
import matplotlib.pyplot as plt
import numpy as np


# sin函数: sin(2 * pi * x)
def sin(x):
    y = torch.sin(2 * math.pi * x)
    return y


def create_toy_data(func, interval, sample_num, noise=0.0, add_outlier=False, outlier_ratio=0.001):
    # 均匀采样
    # 使用torch.rand在生成sample_num个随机数
    X = torch.rand(size=[sample_num]) * (interval[1] - interval[0]) + interval[0]
    y = func(X)

    # 生成高斯分布的标签噪声
    # 使用torch.normal生成0均值，noise标准差的数据
    epsilon = torch.tensor(np.random.normal(0, noise, size=y.shape[0]))
    y = y + epsilon
    if add_outlier:  # 生成额外的异常点
        outlier_num = int(len(y) * outlier_ratio)
        if outlier_num != 0:
            # 使用torch.randint生成服从均匀分布的、范围在[0, len(y))的随机Tensor
            outlier_idx = torch.rand(len(y), shape=[outlier_num])
            y[outlier_idx] = y[outlier_idx] * 5
    return X, y


func = sin
interval = (0, 1)
train_num = 15
test_num = 10
noise = 0.5  # 0.1
X_train, y_train = create_toy_data(func=func, interval=interval, sample_num=train_num, noise=noise)
X_test, y_test = create_toy_data(func=func, interval=interval, sample_num=test_num, noise=noise)

X_underlying = torch.linspace(interval[0], interval[1], steps=100)
y_underlying = sin(X_underlying)

# 绘制图像
plt.rcParams['figure.figsize'] = (8.0, 6.0)
plt.scatter(X_train, y_train, facecolor="none", edgecolor='#e4007f', s=50, label="train data")
plt.scatter(X_test, y_test, facecolor="none", edgecolor="g", s=50, label="test data")
plt.plot(X_underlying, y_underlying, c='#000000', label=r"$\sin(2\pi x)$")
plt.legend(fontsize='x-large')
plt.savefig('ml-vis2.pdf')
plt.show()

运行结果：

 

2.3.2 模型构建

套用求解线性回归参数的方法来求解多项式回归参数

# 多项式转换
def polynomial_basis_function(x, degree=2):
    if degree == 0:
        return torch.ones(shape=x.shape, dtype=torch.float32)

    x_tmp = x
    x_result = x_tmp

    for i in range(2, degree + 1):
        x_tmp = torch.multiply(x_tmp, x)  # 逐元素相乘
        x_result = torch.concat((x_result, x_tmp), axis=-1)

    return x_result


# 简单测试
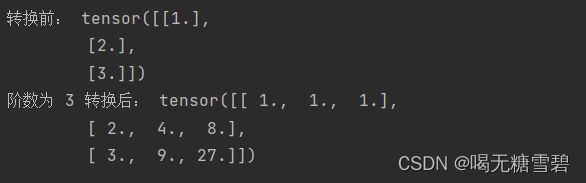
data = [[1], [2], [3]]
X = torch.as_tensor(data=data, dtype=torch.float32)
degree = 3
transformed_X = polynomial_basis_function(X, degree=degree)
print("转换前：", X)
print("阶数为", degree, "转换后：", transformed_X)

运行结果：

2.3.3 模型训练

  for i, degree in enumerate([0, 1, 3, 8]):  # []中为多项式的阶数
    model = Linear(degree)
    X_train_transformed = polynomial_basis_function(X_train.reshape([-1, 1]), degree)
    X_underlying_transformed = polynomial_basis_function(X_underlying.reshape([-1, 1]), degree)
 
    model = optimizer_lsm(model, X_train_transformed, y_train.reshape([-1, 1]))  # 拟合得到参数
 
    y_underlying_pred = model(X_underlying_transformed).squeeze()
 
    print(model.params)
 
    # 绘制图像
    plt.subplot(2, 2, i + 1)
    plt.scatter(X_train, y_train, facecolor="none", edgecolor='#e4007f', s=50, label="train data")
    plt.plot(X_underlying, y_underlying, c='#000000', label=r"$\sin(2\pi x)$")
    plt.plot(X_underlying, y_underlying_pred, c='#f19ec2', label="predicted function")
    plt.ylim(-2, 1.5)
    plt.annotate("M={}".format(degree), xy=(0.95, -1.4))
 
# plt.legend(bbox_to_anchor=(1.05, 0.64), loc=2, borderaxespad=0.)
plt.legend(loc='lower left', fontsize='x-large')
plt.savefig('ml-vis3.pdf')
plt.show()

运行结果：

2.3.4 模型评估

# 训练误差和测试误差
training_errors = []
test_errors = []
distribution_errors = []
 
# 遍历多项式阶数
for i in range(9):
    model = Linear(i)
 
    X_train_transformed = polynomial_basis_function(X_train.reshape([-1, 1]), i)
    X_test_transformed = polynomial_basis_function(X_test.reshape([-1, 1]), i)
    X_underlying_transformed = polynomial_basis_function(X_underlying.reshape([-1, 1]), i)
 
    optimizer_lsm(model, X_train_transformed, y_train.reshape([-1, 1]))
 
    y_train_pred = model(X_train_transformed).squeeze()
    y_test_pred = model(X_test_transformed).squeeze()
    y_underlying_pred = model(X_underlying_transformed).squeeze()
 
    train_mse = mean_squared_error(y_true=y_train, y_pred=y_train_pred).item()
    training_errors.append(train_mse)
 
    test_mse = mean_squared_error(y_true=y_test, y_pred=y_test_pred).item()
    test_errors.append(test_mse)
 
    # distribution_mse = mean_squared_error(y_true=y_underlying, y_pred=y_underlying_pred).item()
    # distribution_errors.append(distribution_mse)
 
print("train errors: \n", training_errors)
print("test errors: \n", test_errors)
# print ("distribution errors: \n", distribution_errors)
 
# 绘制图片
plt.rcParams['figure.figsize'] = (8.0, 6.0)
plt.plot(training_errors, '-.', mfc="none", mec='#e4007f', ms=10, c='#e4007f', label="Training")
plt.plot(test_errors, '--', mfc="none", mec='#f19ec2', ms=10, c='#f19ec2', label="Test")
# plt.plot(distribution_errors, '-', mfc="none", mec="#3D3D3F", ms=10, c="#3D3D3F", label="Distribution")
plt.legend(fontsize='x-large')
plt.xlabel("degree")
plt.ylabel("MSE")
plt.savefig('ml-mse-error.pdf')
plt.show()

运行结果：

对于模型过拟合的情况，可以引入正则化方法，通过向误差函数中添加一个惩罚项来避免系数倾向于较大的取值。

 

degree = 8 # 多项式阶数
reg_lambda = 0.0001 # 正则化系数
 
X_train_transformed = polynomial_basis_function(X_train.reshape([-1,1]), degree)
X_test_transformed = polynomial_basis_function(X_test.reshape([-1,1]), degree)
X_underlying_transformed = polynomial_basis_function(X_underlying.reshape([-1,1]), degree)
 
model = Linear(degree) 
 
optimizer_lsm(model,X_train_transformed,y_train.reshape([-1,1]))
 
y_test_pred=model(X_test_transformed).squeeze()
y_underlying_pred=model(X_underlying_transformed).squeeze()
 
model_reg = Linear(degree) 
 
optimizer_lsm(model_reg,X_train_transformed,y_train.reshape([-1,1]),reg_lambda=reg_lambda)
 
y_test_pred_reg=model_reg(X_test_transformed).squeeze()
y_underlying_pred_reg=model_reg(X_underlying_transformed).squeeze()
 
mse = mean_squared_error(y_true = y_test, y_pred = y_test_pred).item()
print("mse:",mse)
mes_reg = mean_squared_error(y_true = y_test, y_pred = y_test_pred_reg).item()
print("mse_with_l2_reg:",mes_reg)
 
# 绘制图像
plt.scatter(X_train, y_train, facecolor="none", edgecolor="#e4007f", s=50, label="train data")
plt.plot(X_underlying, y_underlying, c='#000000', label=r"$\sin(2\pi x)$")
plt.plot(X_underlying, y_underlying_pred, c='#e4007f', linestyle="--", label="$deg. = 8$")
plt.plot(X_underlying, y_underlying_pred_reg, c='#f19ec2', linestyle="-.", label="$deg. = 8, \ell_2 reg$")
plt.ylim(-1.5, 1.5)
plt.annotate("lambda={}".format(reg_lambda), xy=(0.82, -1.4))
plt.legend(fontsize='large')
plt.savefig('ml-vis4.pdf')
plt.show()
 

运行结果：

2.4 Runner类介绍

机器学习方法流程包括数据集构建、模型构建、损失函数定义、优化器、模型训练、模型评价、模型预测等环节。

为了更方便地将上述环节规范化，我们将机器学习模型的基本要素封装成一个Runner类。

除上述提到的要素外，再加上模型保存、模型加载等功能。

Runner类的成员函数定义如下：

__init__函数：实例化Runner类，需要传入模型、损失函数、优化器和评价指标等；
train函数：模型训练，指定模型训练需要的训练集和验证集；
evaluate函数：通过对训练好的模型进行评价，在验证集或测试集上查看模型训练效果；
predict函数：选取一条数据对训练好的模型进行预测；
save_model函数：模型在训练过程和训练结束后需要进行保存；
load_model函数：调用加载之前保存的模型。

2.5 基于线性回归的波士顿房价预测

使用线性回归来对马萨诸塞州波士顿郊区的房屋进行预测。

实验流程主要包含如下5个步骤：

1）数据处理：包括数据清洗（缺失值和异常值处理）、数据集划分，以便数据可以被模型正常读取，并具有良好的泛化性;
2）模型构建：定义线性回归模型类；
3）训练配置：训练相关的一些配置，如：优化算法、评价指标等；
4）组装训练框架Runner：Runner用于管理模型训练和测试过程；
5）模型训练和测试：利用Runner进行模型训练和测试。
 

2.5.1 数据处理

    2.5.1.2 数据清洗

import pandas as pd # 开源数据分析和操作工具
 
# 利用pandas加载波士顿房价的数据集
data=pd.read_csv(r"boston_house_prices.csv")
# 查看各字段缺失值统计情况
print(data.isna().sum())

运行结果：

 由上面的结果可以知道，波士顿房价预测数据集中不存在缺失值的情况

import matplotlib.pyplot as plt # 可视化工具
 
# 箱线图查看异常值分布
def boxplot(data, fig_name):
    # 绘制每个属性的箱线图
    data_col = list(data.columns)
    
    # 连续画几个图片
    plt.figure(figsize=(5, 5), dpi=300)
    # 子图调整
    plt.subplots_adjust(wspace=0.6)
    # 每个特征画一个箱线图
    for i, col_name in enumerate(data_col):
        plt.subplot(3, 5, i+1)
        # 画箱线图
        plt.boxplot(data[col_name], 
                    showmeans=True, 
                    meanprops={"markersize":1,"marker":"D","markeredgecolor":'#f19ec2'}, # 均值的属性
                    medianprops={"color":'#e4007f'}, # 中位数线的属性
                    whiskerprops={"color":'#e4007f', "linewidth":0.4, 'linestyle':"--"},
                    flierprops={"markersize":0.4},
                    ) 
        # 图名
        plt.title(col_name, fontdict={"size":5}, pad=2)
        # y方向刻度
        plt.yticks(fontsize=4, rotation=90)
        plt.tick_params(pad=0.5)
        # x方向刻度
        plt.xticks([])
    plt.savefig(fig_name)
    plt.show()
 
boxplot(data, 'ml-vis5.pdf')
 

    运行结果：

 

由图可以直观的看出，数据中存在很多的异常值，即超出上下两条杠的部分中的黑圆圈，我们将这些异常值认为是数据集中的“噪声”，并将临界值取代噪声点，从而完成对数据集异常值的处理。

用于替换的代码：

# 四分位处理异常值
num_features=data.select_dtypes(exclude=['object','bool']).columns.tolist()
 
for feature in num_features:
    if feature =='CHAS':
        continue
    
    Q1  = data[feature].quantile(q=0.25) # 下四分位
    Q3  = data[feature].quantile(q=0.75) # 上四分位
    
    IQR = Q3-Q1 
    top = Q3+1.5*IQR # 最大估计值
    bot = Q1-1.5*IQR # 最小估计值
    values=data[feature].values
    values[values > top] = top # 临界值取代噪声
    values[values < bot] = bot # 临界值取代噪声
    data[feature] = values.astype(data[feature].dtypes)
 
# 再次查看箱线图，异常值已被临界值替换（数据量较多或本身异常值较少时，箱线图展示会不容易体现出来）
boxplot(data, 'ml-vis6.pdf')
 

运行结果：

    2.5.1.3 数据集划分

import torch
torch.manual_seed(10)
 
# 划分训练集和测试集
def train_test_split(X, y, train_percent=0.8):
    n = len(X)
    shuffled_indices = torch.randperm(n)  # 返回一个数值在0到n-1、随机排列的1-D Tensor
    train_set_size = int(n * train_percent)
    train_indices = shuffled_indices[:train_set_size]
    test_indices = shuffled_indices[train_set_size:]
 
    X = X.values
    y = y.values
 
    X_train = X[train_indices]
    y_train = y[train_indices]
 
    X_test = X[test_indices]
    y_test = y[test_indices]
 
    return X_train, X_test, y_train, y_test
 
 
X = data.drop(['MEDV'], axis=1)
y = data['MEDV']
 
X_train, X_test, y_train, y_test = train_test_split(X, y)  # X_train每一行是个样本，shape[N,D]

2.5.1.4 特征工程

#特征工程
import torch
X_train = torch.as_tensor(X_train,dtype=torch.float32)
X_test = torch.as_tensor(X_test,dtype=torch.float32)
y_train = torch.as_tensor(y_train,dtype=torch.float32)
y_test = torch.as_tensor(y_test,dtype=torch.float32)
X_min = torch.min(X_train,axis=0)[0]
X_max = torch.max(X_train,axis=0)[0]
X_train = (X_train-X_min)/(X_max-X_min)
X_test  = (X_test-X_min)/(X_max-X_min)
# 训练集构造
train_dataset=(X_train,y_train)
# 测试集构造
test_dataset=(X_test,y_test)

2.5.2 模型构建

#模型构建
from nndl.op import Linear
 
# 模型实例化
input_size = 12
model=Linear(input_size)

2.5.3 完善Runner类

在测试集上使用MSE对模型性能进行评估。

import torch.nn as nn
mse_loss = nn.MSELoss()

import torch
import os
from nndl.opitimizer import optimizer_lsm
class Runner(object):
    def __init__(self, model, optimizer, loss_fn, metric):
        # 优化器和损失函数为None,不再关注
 
        # 模型
        self.model = model
        # 评估指标
        self.metric = metric
        # 优化器
        self.optimizer = optimizer
 
    def train(self, dataset, reg_lambda, model_dir):
        X, y = dataset
        self.optimizer(self.model, X, y, reg_lambda)
 
        # 保存模型
        self.save_model(model_dir)
 
    def evaluate(self, dataset, **kwargs):
        X, y = dataset
 
        y_pred = self.model(X)
        result = self.metric(y_pred, y)
 
        return result
 
    def predict(self, X, **kwargs):
        return self.model(X)
 
    def save_model(self, model_dir):
        if not os.path.exists(model_dir):
            os.makedirs(model_dir)
 
        params_saved_path = os.path.join(model_dir, 'params.pdtensor')
        torch.save(model.params, params_saved_path)
 
    def load_model(self, model_dir):
        params_saved_path = os.path.join(model_dir, 'params.pdtensor')
        self.model.params = torch.load(params_saved_path)
 
 
optimizer = optimizer_lsm

#  optimizer_lsm
def optimizer_lsm(model, X, y, reg_lambda=0):
    N, D = X.shape
    # 对输入特征数据所有特征向量求平均
    x_bar_tran = torch.mean(X, axis=0).T
    # 求标签的均值,shape=[1]
    y_bar = torch.mean(y)
    # torch.subtract通过广播的方式实现矩阵减向量
    x_sub = torch.subtract(X, x_bar_tran)
    # 使用torch.all判断输入tensor是否全0
    if torch.all(x_sub == 0):
        model.params['b'] = y_bar
        model.params['w'] = torch.zeros(shape=[D])
        return model
    # torch.inverse求方阵的逆
    tmp = torch.inverse(torch.matmul(x_sub.T, x_sub) +
                         reg_lambda * torch.eye(num_rows=(D)))
 
    w = torch.matmul(torch.matmul(tmp, x_sub.T), (y - y_bar))
 
    b = y_bar - torch.matmul(x_bar_tran, w)
 
    model.params['b'] = b
    model.params['w'] = torch.squeeze(w, axis=-1)
 
    return model

2.5.4 模型训练

在组装完成Runner之后，我们将开始进行模型训练、评估和测试。首先，我们先实例化Runner，然后开始进行装配训练环境，接下来就可以开始训练了

# 启动训练
runner.train(train_dataset,reg_lambda=0,model_dir=saved_dir)

columns_list = data.columns.to_list()
weights = runner.model.params['w'].tolist()
b = runner.model.params['b'].item()
 
for i in range(len(weights)):
    print(columns_list[i],"weight:",weights[i])
 
print("b:",b)

运行结果：

2.5.5 模型测试

# 加载模型权重
runner.load_model(saved_dir)
mse = runner.evaluate(test_dataset)
print('MSE:', mse.item())

运行结果：

2.5.6 模型预测

runner.load_model(saved_dir)
pred = runner.predict(X_test[:1])
print("真实房价：",y_test[:1].item())
print("预测的房价：",pred.item())

运行结果：

 op文件：

import torch
from nndl.activation import softmax
torch.seed() #设置随机种子

class Op(object):
    def __init__(self):
        pass

    def __call__(self, inputs):
        return self.forward(inputs)

    def forward(self, inputs):
        raise NotImplementedError

    def backward(self, inputs):
        raise NotImplementedError

# 线性算子
class Linear(Op):
    def __init__(self,dimension):
        """
        输入：
           - dimension:模型要处理的数据特征向量长度
        """

        self.dim = dimension

        # 模型参数
        self.params = {}
        self.params['w'] = torch.randn(self.dim,1,dtype=torch.float32)
        self.params['b'] = torch.zeros(1,dtype=torch.float32)

    def __call__(self, X):
        return self.forward(X)

    # 前向函数
    def forward(self, X):
        """
        输入：
           - X: tensor, shape=[N,D]
           注意这里的X矩阵是由N个x向量的转置拼接成的，与原教材行向量表示方式不一致
        输出：
           - y_pred： tensor, shape=[N]
        """

        N,D = X.shape

        if self.dim==0:
            return torch.full(shape=[N,1], fill_value=self.params['b'])
        
        assert D==self.dim # 输入数据维度合法性验证

        # 使用torch.matmul计算两个tensor的乘积
        y_pred = torch.matmul(X,self.params['w'])+self.params['b']
        
        return y_pred

#新增Softmax算子
class model_SR(Op):
    def __init__(self, input_dim, output_dim):
        super(model_SR, self).__init__()
        self.params = {}
        #将线性层的权重参数全部初始化为0
        self.params['W'] = torch.zeros(shape=[input_dim, output_dim])
        #self.params['W'] = torch.normal(mean=0, std=0.01, shape=[input_dim, output_dim])
        #将线性层的偏置参数初始化为0
        self.params['b'] = torch.zeros(shape=[output_dim])
        #存放参数的梯度
        self.grads = {}
        self.X = None
        self.outputs = None
        self.output_dim = output_dim

    def __call__(self, inputs):
        return self.forward(inputs)

    def forward(self, inputs):
        self.X = inputs
        #线性计算
        score = torch.matmul(self.X, self.params['W']) + self.params['b']
        #Softmax 函数
        self.outputs = softmax(score)
        return self.outputs

    def backward(self, labels):
        """
        输入：
            - labels：真实标签，shape=[N, 1]，其中N为样本数量
        """
        #计算偏导数
        N =labels.shape[0]
        labels = torch.nn.functional.one_hot(labels, self.output_dim)
        self.grads['W'] = -1 / N * torch.matmul(self.X.t(), (labels-self.outputs))
        self.grads['b'] = -1 / N * torch.matmul(torch.ones(shape=[N]), (labels-self.outputs))

#新增多类别交叉熵损失
class MultiCrossEntropyLoss(Op):
    def __init__(self):
        self.predicts = None
        self.labels = None
        self.num = None

    def __call__(self, predicts, labels):
        return self.forward(predicts, labels)

    def forward(self, predicts, labels):
        """
        输入：
            - predicts：预测值，shape=[N, 1]，N为样本数量
            - labels：真实标签，shape=[N, 1]
        输出：
            - 损失值：shape=[1]
        """
        self.predicts = predicts
        self.labels = labels
        self.num = self.predicts.shape[0]
        loss = 0
        for i in range(0, self.num):
            index = self.labels[i]
            loss -= torch.log(self.predicts[i][index])
        return loss / self.num

opitimizer文件：

import torch

def optimizer_lsm(model, X, y, reg_lambda=0):
  """
    输入：
       - model: 模型
       - X: tensor, 特征数据，shape=[N,D]
       - y: tensor,标签数据，shape=[N]
       - reg_lambda: float, 正则化系数，默认为0
    输出：
       - model: 优化好的模型
    """

  N, D = X.shape

  # 对输入特征数据所有特征向量求平均
  x_bar_tran = torch.mean(X, dim=0).T
  
  # 求标签的均值,shape=[1]
  y_bar = torch.mean(y)
  
  # torch.subtract通过广播的方式实现矩阵减向量
  x_sub = torch.subtract(X,x_bar_tran)

  # 使用torch.all判断输入tensor是否全0
  if torch.all(x_sub==0):
    model.params['b'] = y_bar
    model.params['w'] = torch.zeros(shape=[D])
    return model
  
  # torch.inverse求方阵的逆
  tmp = torch.inverse(torch.matmul(x_sub.T,x_sub)+reg_lambda*torch.eye(D))

  w = torch.matmul(torch.matmul(tmp,x_sub.T),(y-y_bar))
  
  b = y_bar-torch.matmul(x_bar_tran,w)
  
  model.params['b'] = b
  model.params['w'] = torch.squeeze(w,axis=-1)

  return model

from abc import abstractmethod

#新增优化器基类
class Optimizer(object):
    def __init__(self, init_lr, model):
        """
        优化器类初始化
        """
        #初始化学习率，用于参数更新的计算
        self.init_lr = init_lr
        #指定优化器需要优化的模型
        self.model = model

    @abstractmethod
    def step(self):
        """
        定义每次迭代如何更新参数
        """
        pass

#新增梯度下降法优化器
class SimpleBatchGD(Optimizer):
    def __init__(self, init_lr, model):
        super(SimpleBatchGD, self).__init__(init_lr=init_lr, model=model)

    def step(self):
        #参数更新
        #遍历所有参数，按照公式(3.8)和(3.9)更新参数
        if isinstance(self.model.params, dict):
            for key in self.model.params.keys():
                self.model.params[key] = self.model.params[key] - self.init_lr * self.model.grads[key]

问题1：使用类实现机器学习模型的基本要素有什么优点？
答：使用类实现机器学习模型基本要素方便整洁，更容易被人理解。同时也加强了代码的稳定性和正确性，有利与代码的维护。
问题2：算子op、优化器opitimizer放在单独的文件中，主程序在使用时调用该文件。这样做有什么优点？
答：简化操作，方便备份，以后再用到算子op,优化器opitimizer时可以直接调用
问题3：线性回归通常使用平方损失函数，能否使用交叉熵损失函数？为什么？
答：交叉熵损失函数主要用于离散情况，假设误差是二值分部，平方损失函数是实际值与目标值之间的误差，假设误差服从正态分布。因此线性回归通常使用平方损失函数。

总结：

血泪教训，计算机一定要把基础打牢，多做题，最好不断地将遇到的问题用写笔记或博客的方式记录下来，相信我，下次遇到大概率还是不会，时候就会那感谢自己的笔记了。再次强调——计算机基础一定要打好！打好！打好！不说了，去b站从python基础开始重学去了。