【论文精读】时序逻辑推理之基于梯度的参数优化 TeLEx: Passive STL Learning Using Only Positive Examples
前言:
之前精读了两篇参数学习的文章, 算法的运行效果不尽人意, 并且最终也没有得出最佳参数. 这篇文章提出用优化算法来直接计算出, 因此特地读来看看.
主要参考文献:
Jha, S., Tiwari, A., Seshia, S. A., Sahai, T., & Shankar, N. (2017). TeLEx: Passive STL Learning Using Only Positive Examples. In Runtime Verification (pp. 208–224). https://doi.org/10.1007/978-3-319-67531-2_13
文章目录
- 概览
- 流水账笔记
-
- 1 Introduction
- 2 Priliminaries
- 3 Related Work
-
- Learning STL formula
-
- Active learning/Falsification:
- Gradient-based falsification
- Passive learning
- Metrics for STL Satisfiability
-
- Robustness Metric
- Average Robustness Metric
- Learning from Positive Examples
- 4 Learning STL from Positive Examples
-
- 案例介绍
- 重要定义
- 问题转换
- 求解器
- 5 Experimental Evaluations
-
- 1. Temporal Bounds on Signal x ( t ) = t sin ( t 2 ) x(t)=t\sin(t^2) x(t)=tsin(t2)
- 2. Two Agent Surveillance
- 3. Udacity Autonomous-Car Driving Public Data-set
- 6 Conclusion
-
- 创新点总结
- 未来拓展
- 心得与笔记
概览
本文定义了tightness函数, 将求解临界robustness转换为了求解tightness最大值问题. 并且利用了基于梯度的优化方法提高了运算效率. 最终形成软件成果Python工具包TeLEx.
流水账笔记
1 Introduction
对STL特性的研究主要分为两种:
- Classifier learning: 通过对正负例的划分求STL公式, 并将STL公式作为分类器使用.
- Active learning: 要求系统尝试产生信号来证伪STL公式, 并将此类信号作为反例.
本文研究的是第一类, 但是只是用正例样本. 这与实际的生产场景是一致的, 因为实际获取反例代价太高, 例如飞机坠毁、汽车追尾等等.
本研究的主要问题就是, 在没有负例的情况下如何避免对正例的过度泛化.
本文提出了一种用于量化tightness的指标, 并且用平滑函数来使得基于梯度的优化算法成为可能.
2 Priliminaries
介绍了什么是区间、时间域、STL公式以及STL公式的布尔语义及量化语义.
3 Related Work
Learning STL formula
Active learning/Falsification:
- Robustness-guided temporal logic testing and verification for stochastic cyber-physical systems
- Falsification of Conditional Safety Properties for Cyber-Physical Systems with Gaussian Process Regression
- S-TaLiRo: A Tool for Temporal Logic Falsification for Hybrid Systems
- Querying Parametric Temporal Logic Properties on Embedded Systems
Gradient-based falsification
- Functional gradient descent method for Metric Temporal Logic specifications
Passive learning
- Data-Driven Statistical Learning of Temporal Logic Properties
- A Decision Tree Approach to Data Classification using Signal Temporal Logic
- Temporal logic inference for classification and prediction from data
Metrics for STL Satisfiability
Robustness Metric
- Robust Satisfaction of Temporal Logic over Real-Valued Signals
- Robustness of Temporal Logic Specifications
Average Robustness Metric
- Robust control for signal temporal logic specifications using average space robustness
Learning from Positive Examples
- Language identification in the limit
- A study of grammatical inference
- Identifying languages from stochastic examples
- Learning from positive data
- A theory of the learnable
- A theory of formal synthesis via inductive learning
4 Learning STL from Positive Examples
案例介绍
要学习的公式如下:
ϕ = ∣ ang ∣ ≥ 0.2 ⇒ F [ 0 , 6 ] spd ≤ α \phi=|\text{ang}|\geq 0.2 \Rightarrow F_{[0,6]}\text{spd}\leq \alpha ϕ=∣ang∣≥0.2⇒F[0,6]spd≤α
其中只有一个参数变量 α \alpha α, 此公式表示: 如果汽车方向盘转角超过0.2, 则6秒内速度能够达到的最小值.
重要定义
ϵ \epsilon ϵ-邻域:
N ϵ ( ϕ ( v 1 , v 2 , . . . , v k ) ) = { ϕ ( v 1 ′ , v 2 ′ , . . . , v k ′ ) s . t . ∣ v i − v 1 ′ ∣ ≤ ϵ i f o r 1 ≤ i ≤ k } \mathcal{N}_\epsilon(\phi(v1,v2,...,v_k))=\{\phi(v_1',v_2',...,v_k') s.t. |v_i-v_1'|\leq \epsilon_i for 1\leq i\leq k\} Nϵ(ϕ(v1,v2,...,vk))={ϕ(v1′,v2′,...,vk′)s.t.∣vi−v1′∣≤ϵifor1≤i≤k}
ϵ \epsilon ϵ-tight STL公式:
∀ τ ∈ T : τ ⊨ ϕ ( v 1 ∗ , v 2 ∗ , . . . , v k ∗ ) a n d ∃ τ ∈ T : τ ⊭ ϕ ( v 1 , v 2 , . . . , v k ) \forall \tau \in \mathcal{T}: \tau\models\phi(v_1^*,v_2^*,...,v_k^*)\\ and\\ \exists \tau \in \mathcal{T}: \tau \not\models \phi(v_1,v_2,...,v_k) ∀τ∈T:τ⊨ϕ(v1∗,v2∗,...,vk∗)and∃τ∈T:τ⊨ϕ(v1,v2,...,vk)
问题转换
越tight的参数选择, 其 ϵ \epsilon ϵ邻域越小, 因此求解tightest公式的问题转换为了以下问题:
minimize { ∣ ϵ 1 ∣ , ∣ ϵ 2 ∣ , … , ∣ ϵ k ∣ } s.t. ϵ 1 = p 1 − p 1 ′ , ϵ 2 = p 2 − p 2 ′ , … , ϵ k = p k − p k ′ ∀ τ ∈ T τ ⊨ ϕ ( p 1 , p 2 , … , p k ) , ∃ τ ′ ∈ T τ ′ ⊨ ϕ ( p 1 ′ , p 2 ′ , … , p k ′ ) \begin{gathered} \operatorname{minimize}\left\{\left|\epsilon_{1}\right|,\left|\epsilon_{2}\right|, \ldots,\left|\epsilon_{k}\right|\right\} \text { s.t. } \\ \epsilon_{1}=p_{1}-p_{1}^{\prime}, \epsilon_{2}=p_{2}-p_{2}^{\prime}, \ldots, \epsilon_{k}=p_{k}-p_{k}^{\prime} \\ \forall \tau \in \mathcal{T} \tau \models \phi\left(p_{1}, p_{2}, \ldots, p_{k}\right), \exists \tau^{\prime} \in \mathcal{T} \tau^{\prime} \models \phi\left(p_{1}^{\prime}, p_{2}^{\prime}, \ldots, p_{k}^{\prime}\right) \end{gathered} minimize{∣ϵ1∣,∣ϵ2∣,…,∣ϵk∣} s.t. ϵ1=p1−p1′,ϵ2=p2−p2′,…,ϵk=pk−pk′∀τ∈Tτ⊨ϕ(p1,p2,…,pk),∃τ′∈Tτ′⊨ϕ(p1′,p2′,…,pk′)
那么问题就变成了一个多参数的优化问题, 在现实中很难进行求解. 并且约束中需要验证是否满足的计算是一个NP难问题, 因此用STL的鲁棒语义替换:
minimize { ∣ ϵ 1 ∣ , ∣ ϵ 2 ∣ , … , ∣ ϵ k ∣ } s.t. ϵ 1 = p 1 − p 1 ′ , ϵ 2 = p 2 − p 2 ′ , … , ϵ k = p k − p k ′ ∀ τ ∈ T ρ ( ϕ ( p 1 , p 2 , … , p k ) , τ , 0 ) ≥ 0 , ∃ τ ′ ∈ T ρ ( ϕ ( p 1 ′ , p 2 ′ , … , p k ′ ) , τ ′ , 0 ) < 0 \begin{gathered} \text { minimize }\left\{\left|\epsilon_{1}\right|,\left|\epsilon_{2}\right|, \ldots,\left|\epsilon_{k}\right|\right\} \quad \text { s.t. } \\ \epsilon_{1}=p_{1}-p_{1}^{\prime}, \epsilon_{2}=p_{2}-p_{2}^{\prime}, \ldots, \epsilon_{k}=p_{k}-p_{k}^{\prime} \\ \forall \tau \in \mathcal{T} \rho\left(\phi\left(p_{1}, p_{2}, \ldots, p_{k}\right), \tau, 0\right) \geq 0, \exists \tau^{\prime} \in \mathcal{T} \rho\left(\phi\left(p_{1}^{\prime}, p_{2}^{\prime}, \ldots, p_{k}^{\prime}\right), \tau^{\prime}, 0\right)<0 \end{gathered} minimize {∣ϵ1∣,∣ϵ2∣,…,∣ϵk∣} s.t. ϵ1=p1−p1′,ϵ2=p2−p2′,…,ϵk=pk−pk′∀τ∈Tρ(ϕ(p1,p2,…,pk),τ,0)≥0,∃τ′∈Tρ(ϕ(p1′,p2′,…,pk′),τ′,0)<0
然而现在还是一个多变量优化问题, 还需要进一步转化. 由于鲁棒性在参数空间是连续的, 因此 ϵ \epsilon ϵ越小就是鲁棒性越低. 问题进一步简化为以下:
minimize e p 1 , p 2 , … , p k min τ ∈ T ∣ ρ ( ϕ ( p 1 , p 2 , … , p k ) , τ , 0 ) ∣ \operatorname{minimize} e_{p_{1}, p_{2}, \ldots, p_{k}} \min _{\tau \in \mathcal{T}}\left|\rho\left(\phi\left(p_{1}, p_{2}, \ldots, p_{k}\right), \tau, 0\right)\right| minimizeep1,p2,…,pkτ∈Tmin∣ρ(ϕ(p1,p2,…,pk),τ,0)∣
简化到现在还存在一个问题, 上式中的 ∣ ⋅ ∣ |\cdot| ∣⋅∣把鲁棒度的符号消去了, 即使最终得到的鲁棒性接近于零, 只要其符号是负的 (如下图 (a) ) , 那么信号还是不能满足所求STL公式. 我们希望找到的参数应该使得鲁棒度无限接近零但是稍微大于零.

因此进行最后一步转化: 定义tightness指标 θ ( μ , τ , t ) \theta(\mu,\tau,t) θ(μ,τ,t), 将鲁棒度 r r r进行非线性映射, 强行把两种情况分开, 理想的tightness函数如上图 (b) 所示, 但是只能用类似于图 © 的函数来近似.
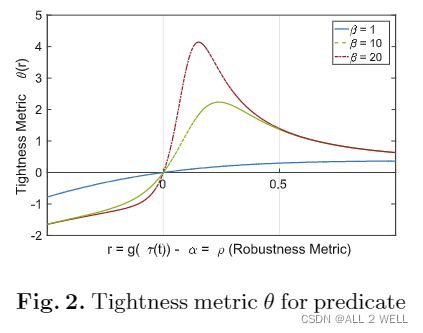
最后选择的 θ ( r ) \theta(r) θ(r)如上图所示, 其函数定义为:
1 r + e − β r − e − r \frac{1}{r+e^{-\beta r}}-e^{-r} r+e−βr1−e−r
其中 β \beta β是决定曲线陡峭度的参数, β ≥ 1 \beta\geq 1 β≥1, 取不同数值具体效果如Fig.2所示. 由于 r ( α , τ , 0 ) r(\alpha,\tau,0) r(α,τ,0)连续, θ ( r ) \theta(r) θ(r)平滑, 因此复合函数 θ ( α , τ , t ) \theta(\alpha,\tau,t) θ(α,τ,t)也是平滑的, 因此就可以使用基于梯度的优化方法来求解最大值.
上面演示的是不包含时序操作子的公式的处理方式, 当包含时序操作子时,
对于 G [ t 2 − t 1 ] ϕ G_{[t_2-t_1]\phi} G[t2−t1]ϕ, 时间间隔 t 2 − t 1 t_2-t_1 t2−t1越大, robustness越小; 对于 F [ t 2 − t 1 ] ϕ F_{[t_2-t_1]\phi} F[t2−t1]ϕ, 时间间隔 t 2 − t 1 t_2-t_1 t2−t1越大, robustness越大. 为了抵消这样的影响, 要乘以一个系数消除一下.

其中, globally操作子的系数函数为 C ( γ , t 1 , t 2 ) = 2 1 + e γ ( t 2 − t 1 + 1 ) C(\gamma,t_1,t_2)=\frac{2}{1+e^{\gamma(t_2-t_1+1)}} C(γ,t1,t2)=1+eγ(t2−t1+1)2, finally操作子的系数函数为 E ( γ , t 1 , t 2 ) = 2 1 + e − γ ( t 2 − t 1 + 1 ) E(\gamma,t_1,t_2)=\frac{2}{1+e^{-\gamma(t_2-t_1+1)}} E(γ,t1,t2)=1+e−γ(t2−t1+1)2. 其中 γ ≥ 0 \gamma \geq 0 γ≥0的数值体现了对时间参数的偏好. C C C使得tightness更小, 因此更容易得到更大的时间间隔 t 2 − t 1 t_2-t_1 t2−t1; 相反 E E E使得tightness更大, 容易得到更大的时间间隔 t 2 − t 1 t_2-t_1 t2−t1.
最终, 我们的问题转换为了:
对于单个信号:
( v 1 ∗ , v 2 ∗ , … , v k ∗ ) = arg max p 1 , p 2 , … , p k θ ( ϕ ( p 1 , p 2 , … , p k ) , τ , 0 ) \left(v_{1}^{*}, v_{2}^{*}, \ldots, v_{k}^{*}\right)=\arg \max _{p_{1}, p_{2}, \ldots, p_{k}} \theta\left(\phi\left(p_{1}, p_{2}, \ldots, p_{k}\right), \tau, 0\right) (v1∗,v2∗,…,vk∗)=argp1,p2,…,pkmaxθ(ϕ(p1,p2,…,pk),τ,0)
对于整个数据集:
( v 1 ∗ , v 2 ∗ , … , v k ∗ ) = arg max p 1 , p 2 , … , p k [ min τ ∈ T θ ( ϕ ( p 1 , p 2 , … , p k ) , τ , 0 ) ] \left(v_{1}^{*}, v_{2}^{*}, \ldots, v_{k}^{*}\right)=\arg \max _{p_{1}, p_{2}, \ldots, p_{k}}\left[\min _{\tau \in \mathcal{T}} \theta\left(\phi\left(p_{1}, p_{2}, \ldots, p_{k}\right), \tau, 0\right)\right] (v1∗,v2∗,…,vk∗)=argp1,p2,…,pkmax[τ∈Tminθ(ϕ(p1,p2,…,pk),τ,0)]
求解器
这篇文章选择了拟牛顿法来求解优化问题, 这是一个基于梯度的优化算法差分进化法. 同时还用了不基于梯度的算法差分进化法来验证效果.
5 Experimental Evaluations
1. Temporal Bounds on Signal x ( t ) = t sin ( t 2 ) x(t)=t\sin(t^2) x(t)=tsin(t2)
尝试学习公式: ⋀ i = 0 k ( G [ i , i + 1 ] ( x ≤ p 2 i ∧ x ≥ p 2 i + 1 ) ) , k = 0 , 1 , . . . , 11 \bigwedge_{i=0}^{k}\left(G_{[i, i+1]}\left(x \leq p_{2 i} \wedge x \geq p_{2 i+1}\right)\right), k=0,1,...,11 ⋀i=0k(G[i,i+1](x≤p2i∧x≥p2i+1)),k=0,1,...,11
由于优化算法有随机性, 因此每个算法跑10遍, 下面的图像记录了实验结果. 图 (b) © 中的误差柱表示runtime的标准差.

上图显示, 基于梯度的方法提速了30-100倍. 并且, 基于梯度方法学习到的公式的robustness更小.
2. Two Agent Surveillance
下面给了两个卫兵巡逻的例子. 两个卫兵的初始位置在左下角和右上角. 在每个时刻, 卫兵会计算从他们当前位置到入侵者的距离,然后他们选择离他们最近的入侵者作为目标并朝着它移动. 如果移动的过程中冒出来一个新的入侵者, 那么卫兵的目标可能因为距离这个新的入侵者而变化. 当卫兵移动到入侵者的位置时, 入侵者被消灭,之后卫兵就一定停留到新的入侵者出现. 同一时刻最多只有两个入侵者.
取仿真1000步进行训练, 学到两条STL特性:
- 入侵者出现到被消灭的最大时间为39.001.
- 两个agent的最小距离为4.998. 说明采取的“就近原则”能够避免卫兵相撞.
这个案例不是特别懂, 作者也没有将具体的公式写出来.
3. Udacity Autonomous-Car Driving Public Data-set
这个案例使用了Udacity智能驾驶公共数据集. 使用的HMB-1数据集包括了13205个长度为221s的信号样本, 使用了方向盘转角、扭矩和速度三个维度的数据. 学习了以下STL公式:
- 汽车急转弯时的最大安全速度
模板: G [ 0 , 2.2 e 11 ] ( ( ( G[0,2.2 e 11]((( G[0,2.2e11]((( angle ≥ 0.2 ) ∣ ( \geq 0.2) \mid( ≥0.2)∣( angle ≤ − 0.2 ) ) ⇒ ( \leq-0.2)) \Rightarrow( ≤−0.2))⇒( speed ≤ a ? 15 ; 25 ) ) \leq a ? 15 ; 25)) ≤a?15;25))
结果: G [ 0.0 , 2.2 e 11 ] ( ( ( G[0.0,2.2 e 11]((( G[0.0,2.2e11]((( angle ≥ 0.2 ) ∣ ( \geq 0.2) \mid( ≥0.2)∣( angle ≤ − 0.2 ) ) ⇒ ( \leq-0.2)) \Rightarrow( ≤−0.2))⇒( speed ≤ 22.01 ) ) \leq 22.01)) ≤22.01))
Tightness=0.067, robustness=0.004, runtime=8.64s
- 突然给大扭矩瞬间行驶的最大安全速度
模板: G [ 0 , 2.2 e 11 ] ( ( ( G[0,2.2 e 11]((( G[0,2.2e11]((( torque ≥ 1.6 ) ∣ ( \geq 1.6) \mid( ≥1.6)∣( torque ≤ − 1.6 ) ) ⇒ ( \leq-1.6)) \Rightarrow( ≤−1.6))⇒( speed ≤ a ? 15 ; 25 ) ) \leq a ? 15 ; 25)) ≤a?15;25))
结果: G [ 0.0 , 2.2 e 11 ] ( ( ( G[0.0,2.2 e 11]((( G[0.0,2.2e11]((( torque ≥ 1.6 ) ∣ ( \geq 1.6) \mid( ≥1.6)∣( torque ≤ − 1.6 ) ) ⇒ ( \leq-1.6)) \Rightarrow( ≤−1.6))⇒( speed ≤ 23.64 ) ) \leq 23.64)) ≤23.64))
Tightness=0.221, robustness=0.005, runtime=10.12s
- 大转弯时应该施加的最小的反向扭矩
模板: G [ 0 , 2.2 e 11 ] ( ( G[0,2.2 e 11](( G[0,2.2e11](( angle ≥ 0.06 ) ⇒ ( \geq 0.06) \Rightarrow( ≥0.06)⇒( torque ≥ b ? − 2 ; − 0.5 ) ) \geq b ?-2 ;-0.5)) ≥b?−2;−0.5))
结果: G [ 0.0 , 2.2 e 11 ] ( ( G[0.0,2.2 e 11](( G[0.0,2.2e11](( angle ≥ 0.06 ) ⇒ ( \geq 0.06) \Rightarrow( ≥0.06)⇒( torque ≥ − 1.06 ) ) \geq-1.06)) ≥−1.06))
Tightness=0.113, robustness=0.003, runtime=7.30s
- 小转弯时应当施加的最大正向扭矩
模板: G [ 0 , 2.2 e 11 ] ( ( G[0,2.2 e 11](( G[0,2.2e11](( angle ≤ − 0.06 ) ⇒ ( \leq-0.06) \Rightarrow( ≤−0.06)⇒( torque ≤ b ? 0.5 ; 2 ) ) \leq b ? 0.5 ; 2)) ≤b?0.5;2))
结果: G [ 0.0 , 2.2 e 11 ] ( ( G[0.0,2.2 e 11](( G[0.0,2.2e11](( angle ≤ − 0.06 ) ⇒ ( \leq-0.06) \Rightarrow( ≤−0.06)⇒( torque ≤ 1.25 ) ) \leq 1.25)) ≤1.25))
Tightness=0.472, robustness=0.002, runtime=5.00s
- 反向扭矩的施加将方向盘转角减小到的最大值
模板: G [ 0 , 2.2 e 11 ] ( ( G[0,2.2 e 11](( G[0,2.2e11](( torque ≤ 0.0 ) ⇒ F [ 0.0 , 1.2 e 8 ] ( \leq 0.0) \Rightarrow F[0.0,1.2 e 8]( ≤0.0)⇒F[0.0,1.2e8]( angle ≤ a ? − 1 ; 1 ) ) \leq a ?-1 ; 1)) ≤a?−1;1))
结果: G [ 0.0 , 2.2 e 11 ] ( ( G[0.0,2.2 e 11](( G[0.0,2.2e11](( torque ≤ 0.0 ) ⇒ F [ 0.0 , 1.2 e 8 ] ( \leq 0.0) \Rightarrow F[0.0,1.2 e 8]( ≤0.0)⇒F[0.0,1.2e8]( angle ≤ 0.01 ) ) \leq 0.01)) ≤0.01))
Tightness=0.727, robustness=0.002, runtime=46.59s
从上面可以看到得到的robustness都非常低, 运行时间也可以接受. 最后一个可能是因为有两个时序操作子, 所以计算时间明显变长. 上面的公式可以作为判别安全行为的标准, 也可以用来比较不同的自动驾驶策略.
6 Conclusion
创新点总结
- 提出了tightness (平滑函数) 的度量方法
- 融合了对于某一参数的优化优先级
- 采用了基于梯度的优化方法
未来拓展
- 探究其他量化指标
心得与笔记
- 理论可行, 但是实际实验的时候都只学了一个参数, 没有给出既学习时间参数又学习尺度参数的例子, 是不是计算效率还是跟不上啊.
- tightness的计算中还是有min或max操作子, 还是会使函数不连续, 因此这篇文章的证明不是太完备啊.
