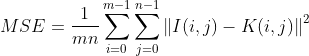DPCM编码算法的实现与分析

目录

DPCM编解码原理

DPCM编码系统的设计

量化误差PSNR

DPCM

main.cpp

实验结果

实验总结

---

DPCM编解码原理

 

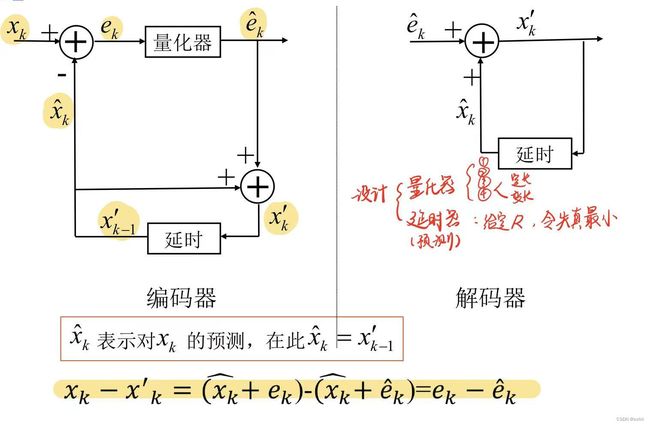
DPCM是差分预测编码调制的缩写，是比较典型的预测编码系统。在DPCM系统中，需要注意的是预测器的输入是已经解码以后的样本。之所以不用原始样本来做预测，是因为在解码端无法得到原始样本，只能得到存在误差的样本。因此，在DPCM编码器中实际内嵌了一个解码器，如编码器中虚线框中所示。在一个DPCM系统中，有两个因素需要设计：预测器和量化器。理想情况下，预测器和量化器应进行联合优化。实际中，采用一种次优的设计方法：分别进行线性预测器和量化器的优化设计。

DPCM编码系统的设计

在本次实验中，我们采用固定预测器和均匀量化器。预测器采用左侧、上方预测均可。

量化器采用8比特均匀量化。本实验的目标是验证DPCM编码的编码效率。首先读取一个256级的灰度图像，采用自己设定的预测方法计算预测误差，并对预测误差进行8比特均匀量化（基本要求）。还可对预测误差进行1比特、2比特和4比特的量化设计（提高要求）。在DPCM编码器实现的过程中可同时输出预测误差图像和重建图像。将预测误差图像写入文件并将该文件输入Huffman编码器，得到输出码流、给出概率分布图并计算压缩比。将原始图像文件输入Huffman编码器，得到输出码流、给出概率分布图并计算压缩比。最后比较两种系统（1.DPCM+熵编码和2.仅进行熵编码）之间的编码效率（压缩比和图像质量）。压缩质量以PSNR进行计算。

量化误差PSNR

计算量化误差时需要计算其均方误差MSE。若图像大小为M×N，I与K分别为原图像和重建图像，则其均方误差计算公式为：

 对于图像数据的量化，实验使用峰值信噪比PSNR进行描述。对像素Y分量最大值为255的灰度图像来说，其峰值信噪比（单位为dB）的计算公式如下：

 PSNR值越大，代表效果越理想。

//计算压缩质量
void PSNR(unsigned char* ori_yBuf, unsigned char* rec_yBuf, int width, int height) {
	double psnr = 0, MSE = 0;
	for (int i = 0; i < height; i++)
	{
		for (int j = 0; j < width; j++) {
			MSE += (ori_yBuf[i * width + j] - rec_yBuf[i * width + j]) * (ori_yBuf[i * width + j] - rec_yBuf[i * width + j]);
		}
	}
	MSE = MSE / (height * width);
	double MAX = 255;
	psnr = 10 * log10((MAX * MAX) / MSE);
	cout << "psnr=" << psnr << endl;
}

DPCM

//预测+量化
void DPCM(unsigned char* ori_yBuf, unsigned char* pre_yBuf, unsigned char* rec_yBuf, int width, int height, int bitdepth)
{
	double num = pow(2, (int)(9 - bitdepth));
	for (int i = 0; i < height; i++)    //每一行
	{
		for (int j = 0; j < width; j++)  //第一列
		{
			if (j == 0) //使用左侧预测的方法，第一列的像素没有参考值
			{
				//假设预测值为128
				//计算预测误差，对预测误差进行量化
				pre_yBuf[i * width] = (unsigned char)(((ori_yBuf[i * width] - 128) + 255) / num);
				//计算重建值，重建值=反量化后的误差+预测值
				rec_yBuf[i * width] = (unsigned char)((pre_yBuf[i * width] - 255 / num) * num + 128);


			}
			else
			{   //选取前一像素的重建值作为预测值
				//计算预测误差，对预测误差进行量化
				pre_yBuf[i * width + j] = (unsigned char)(((ori_yBuf[i * width + j] - rec_yBuf[i * width + j - 1]) + 255) / num);
				//计算重建值，重建值=反量化后的误差+预测值
				rec_yBuf[i * width + j] = (unsigned char)((pre_yBuf[i * width + j] - 255 / num) * num + rec_yBuf[i * width + j - 1]);

			}
			//防止溢出
			pre_yBuf[i * width + j] = (unsigned char)(pre_yBuf[i * width + j] * num / 2);
			if (rec_yBuf[i * width + j] > 255)
				rec_yBuf[i * width + j] = 255;
			if (rec_yBuf[i * width + j] < 0)
				rec_yBuf[i * width + j] = 0;

		}
	}

}

main.cpp

int main(int argc, char* argv[])
{
	char* ori_yuvfilename = NULL;
	char* pre_yuvfilename = NULL;
	char* rec_yuvfilename = NULL;

	FILE* ori_y_file = NULL;
	FILE* pre_y_file = NULL;
	FILE* rec_y_file = NULL;

	int width, height, bitdepth;

	ori_yuvfilename = argv[1];
	pre_yuvfilename = argv[2];
	rec_yuvfilename = argv[3];
	width = atoi(argv[4]);
	height = atoi(argv[5]);
	bitdepth = atoi(argv[6]);


	unsigned char* u_buffer = NULL;
	unsigned char* v_buffer = NULL;
	unsigned char* y_buffer = NULL;     //原始图像
	unsigned char* rec_y_buffer = NULL; //重建图像
	unsigned char* pre_y_buffer = NULL; //预测误差

	errno_t err;
	if ((err = fopen_s(&ori_y_file, ori_yuvfilename, "rb")) != 0) {
		cout << "FAIL TO OPEN YUV FILE!";
		exit(1);
	}
	if ((err = fopen_s(&pre_y_file, pre_yuvfilename, "wb")) != 0) {
		cout << "FAIL TO OPEN PRE_YUV FILE!";
		exit(1);
	}
	if ((err = fopen_s(&rec_y_file, rec_yuvfilename, "wb")) != 0) {
		cout << "FAIL TO OPEN REC_YUV FILE!";
		exit(1);
	}

	//开辟空间
	y_buffer = (unsigned char*)malloc(width * height);
	u_buffer = (unsigned char*)malloc(width * height / 4);
	v_buffer = (unsigned char*)malloc(width * height / 4);

	pre_y_buffer = (unsigned char*)malloc(width * height);
	rec_y_buffer = (unsigned char*)malloc(width * height);

	if (y_buffer == NULL || u_buffer == NULL || v_buffer == NULL || pre_y_buffer == NULL || rec_y_buffer == NULL) {
		cout << "no enought memory\n";
		exit(1);
	}

	//读取原始图像数据
	fread(y_buffer, 1, width * height, ori_y_file);
	fread(u_buffer, 1, width * height / 4, ori_y_file);
	fread(v_buffer, 1, width * height / 4, ori_y_file);

	//得到原始图像的灰度值分布
	FILE* orig;

	if ((err = fopen_s(&orig, "ori.txt", "wb")) != 0) {
		cout << "FAIL TO OPEN TXT FILE!";
		exit(1);
	}
	double frequency[256] = { 0 };
	GetFrequency(y_buffer, frequency, height, width);
	for (int i = 0; i < 256; i++)
	{
		fprintf(orig, "%d\t%f\n", i, frequency[i]);
	}


	DPCM(y_buffer, pre_y_buffer, rec_y_buffer, width, height, bitdepth);
	PSNR(y_buffer, rec_y_buffer, width, height);

	FILE* pre;

	if ((err = fopen_s(&pre, "pre.txt", "wb")) != 0) {
		cout << "FAIL TO OPEN TXT FILE!";
		exit(1);
	}
	double frequency_pre[256] = { 0 };
	GetFrequency(pre_y_buffer, frequency_pre, height, width);
	for (int i = 0; i < 256; i++)
	{
		fprintf(pre, "%d\t%f\n", i, frequency_pre[i]);
	}


	//写入重建图像
	fwrite(rec_y_buffer, width * height, 1, rec_y_file);
	fwrite(u_buffer, width * height / 4, 1, rec_y_file);
	fwrite(v_buffer, width * height / 4, 1, rec_y_file);

	//写入预测图像
	fwrite(pre_y_buffer, width * height, 1, pre_y_file);
	fwrite(u_buffer, width * height / 4, 1, pre_y_file);
	fwrite(v_buffer, width * height / 4, 1, pre_y_file);

	free(y_buffer);
	free(u_buffer);
	free(v_buffer);
	free(pre_y_buffer);
	free(rec_y_buffer);

	fclose(ori_y_file);
	fclose(pre_y_file);
	fclose(rec_y_file);

	return 0;
}

实验结果

PSNR约为26.0563

实验总结

PSNR ≥ 40dB时，图像质量非常好，接近于原图像；
30dB ≤ PSNR < 40dB时，图像有可察觉的失真，但质量仍可接受；
20dB ≤ PSNR < 30dB时，图像质量较差；
PSNR < 20dB时，图像质量已经无法接受。