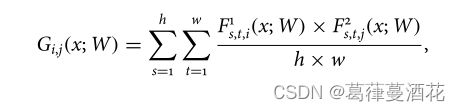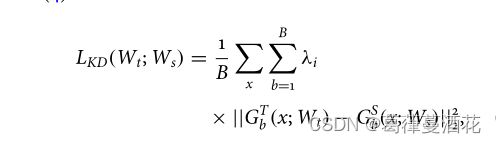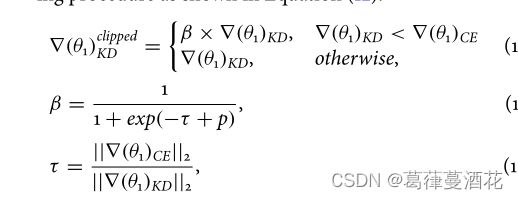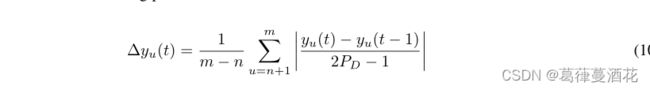(学习笔记)关于KL散度的应用

                                                                                                                                                             

在pca算法中，使用到了一种信息论的理念即KL散度，它对提高模型的可解释性有显著的足以用，同时KL散度在估计两个模型之间的差异性方面也有非常大的作用，简单来说KL散度，就是通过两个模型之间信息熵的差值的期望，来实现评估的作用，它可以实现模型、公式、算法的优化，下面通过几篇文章来，加深对KL散度的理解。                                                                                                                                                         

一、kl散度以及核函数Kernel

首先我们先给出kernel的定义：核函数(kernel function)就是指K(x,y)=，其中x和y是n维的输入值，f()指的是n维到m维的映射(通常m>>n)，即x和y的内积。

其核函数仍是对低维的x,y进行计算，实现在低维下计算出高维映射后的内积结果。本身只是一种简化对应高维下内积的计算方法，核函数可以直接通过原始维度的特征向量来计算得到维度拓展后的向量的镍基，而这种映射关系就是金额函数，并不负责低维到高维的映射(kernel目的不是为了升维，而是为了升维后的简化计算)

目前常用的核函数有：

1.线性内核
Linear内核是最简单的内核函数。它由内积加上一个可选的常数c给出。使用线性内核的内核算法通常等同于非内核对应物，即具有线性内核的KPCA与标准PCA相同。
2.多项式核

多项式内核是一个非固定内核。多项式内核非常适合于所有训练数据都被标准化的问题。

可调参数是斜率α，常数项c和多项式度d。

3.高斯核
高斯核是径向基函数核的一个例子。

或

注意：KL散度不是距离将KL散度视为距离度量可能很诱人，但是我们不能使用KL散度来测量两个分布之间的距离。这是因为KL散度不是对称的。

即 (p||q) 不一定等于 (q||p)

二、Sample selection based on K-L divergence for effectively training SVM（基于K-L散度的样本选择有效训练SVM）

本篇论文质量较一般，他利用了概率神经网络、SVM以及KL散度

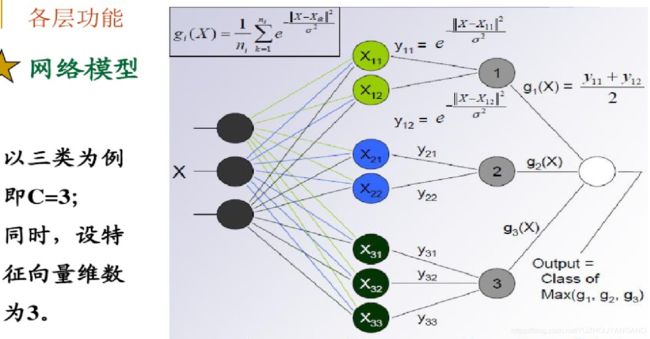
概率神经网络

可以看出他的Kernel使用的为高斯核

本文模型图

它基于以上的图应用KL的思想去选择合适的子集。

他先将子集划分为n+1个子集，之后用每个子集训练一个概率神经网络，之后应用KL的思想，用已有的知识或标准库作为B集合，之后每个子集的结果与标准B进行KL散度的判断估计，注意此过程中每个子集与B判断的结果使用了其平均值作为最后结果。

通过这种方式实现了最子集的筛选提炼。

最后使用筛选过后的集合，没有了非支持向量样本。

使用提纯后的数据集训练SVM,以此来解决SVM在大型数据集合上效率低下的问题。

 三、   Cross-layer knowledge distillation with KL divergence and offline ensemble for compressing deep neural network    （基于kL散度和跨层特征提取对神经网络进行压缩） 

1）一些前置知识

Gram Matrix:简言之Gram Matrix就是k个特征向量之间的内积组成的矩阵——可以被看作feature之间的偏心协方差矩阵（没有减去均值）。

feature map：为了学习对象的feature。假设我们100种滤波器（通道），每种滤波器（通道）的参数不一样，表示它提出输入图像的不同特征。如：边缘、条纹等。

这样每种滤波器去卷积图像就得到对图像的不同特征，我们称之为Feature Map。所以100种卷积核就有100个Feature Map。这100个Feature Map就组成了一层神经元。一般来说浅层网络提取的是局部的细节纹理特征，深层网络提取的是更抽象的轮廓、大小等信息。这些特征总的结合起来表现出来的感觉就是图像的风格。Feature Map中，每个数字都来自于一个特定滤波器filter或者核kernel在特定位置的卷积，因此每个数字代表一个特征的强度。本质就是特征的提取量化。进一步得到这些特征向量后，就可以计算Gram Matrix。

一般来说如果两张feature map 的Gram Matrix的差值较小我们就可以认为两张feature map近似。

FSP模型：简单来说这个模型就是使用一个教师网络（T-DNN）去训练一个学生网络（S-DNN）

3)

本文拟解决的问题：深度神经网络太过复杂，使得他解决一些现实问题是显得太过臃肿，损耗巨大且效率低下。

于是本文选择使用FSP模型并使用跨层特征提取以及KL散度对其进行优化，通过一个复杂臃肿但效果好的网络去训练一个轻便有效的网络。

而上述两种优化的本质就是使得T-DNN与S-DNN尽可能的相似

2）本文提出的模型

1、对于Cross-layer Martix 的理解

 

如上图以及公式，对于一个网络在处理图片的卷积提取过程中，他可以隔一层计算一次Gram Matrix，也可以隔两层计算一次Gram Matrix，又或者是隔三层。本文则对于隔1，2，3.....n均进行计算，之后将T-DNN结果与S-DNN结果做差值，以此作为损失函数的一部分，这样实现对训练过程中对每一层的监督。

2、KL散度的应用

本文的模型采用的是双监督模式，不仅对训练过程加入损失函数进行监督，同时应用KL散度对最后的预测结果进行监督。

用以上公式来计算概率分布，其中 为神经网络最后的sorftmax层的输出。

 

 KL散度：D是来自于C中的一个子集。

最终的损失函数：

对于以及使用了他的平均值

 :最后预测结果与正确标签之间的交叉熵误差。

同时由于比大很多为了防止梯度爆炸，做了如下操作

 

四、SEMI-SUPERVISED ANOMALY DETECTION ALGORITHM BASED ON KL DIVERGENCE (SAD-KL)（基于KL散度的半监督异常检测算法（SAD-KL））

1)前置知识

LOF评分：已知基于 k 个相邻样本之间的相对距离的 LOF 评分在多模态正态性情况下表现出稳健的性能

所以本文只用LOF评分来计算数据集的合格程度即

计算流程：(1)计算p与多个相邻样本的k-distances,(2)计算多个相邻样本之间的k-distances(3)将二者分别取平均值并求其比值（注：本文我们为了更好的效果取了较大的K值）

2）具体算法

一般来说，我们使用半监督学习的时候，一定会遇到这样的问题，我们一直假设有标签的部分与没有标签的部分具有相同的分布，并在这个前提之下使用有标签的集合训练模型，之后再用训练好的模型判断没有标签的数据集。

但这个模式存在先天的问题，我们默认的假设不一定总是成立的，如果假设不成立。那么就会出现局部离群数据（LOF），这对我们的模型判断的准确度产生了非常大的影响。

而KL散度是一个很好的工具，他可以用于估计两个数据集概率密度（PDF）之间的差异，而本文将这种思想融入了模型的生成实现。

 上图为本文的创新算法SAD-KL与传统算法SAD-PL的流程图的比较图。

关于SAD-PL算法，他建设有标签和没有标签的数据集均是正态分布，并在此基础上做出一系列改进，从一定程度上解决了，半监督学习中存的有标签、无标签数据的分布不匹配问题，但从一般角度来说，这样的优化泛用性还是不高。我们无法保证一定所有数据都满足正态分布。

然后是本文提出的SAD-KL算法，他的大题流程与SAD-PL类似，但存在着重大的不同之处。

首先该算法，将数据x输入一个自编码器（没有解码过程的自编码器），得出其特征表示,之后再不进行解码的前提下关闭其潜在质心（防止局部最优解）。之后通过估计的KL散度训练SAD-KL模型，训练模型的过程中，他使用了有标记数据的PDF和通过LOF计算取得的无标签数据。

上面的公式代表的是：再H0的条件下获取s的概率密度，我们可以看出的取值与阈值相关。

 当未标记数据的分布与标记正常数据的分布几乎相同时，从标记正常数据获得的阈值 η 可以对未标记数据给出几乎相同的检测概率。但是，如果未标记的数据包含不同的正态样本，使其具有不同的分布，则在预先从标记数据中获得的阈值 η 下，无法保证相同的检测概率 。为了考虑计算 P的分布差异，本文KL 散度，并采用指数函数将获得的 KL 散度映射到概率值。

 

这里的,而则是一个超参数。我们全部的工作就是，是的上面两个等式相等，估计出阈值，这样就相当于找到了分布近似的有标签数据以及无标签数据，这样就可以很好的训练完善模型，提高模型判断的准确性。

算法流程：

 

关于​​​​​​​的计算方法如下: