小样本学习记录————相似性计算经典网络结构(孪生网络、匹配网络、原型网络、 关系网络)
小样本学习记录————四种相似性计算经典网络结构
- 小样本学习记录————四种相似性计算经典网络结构
-
- 孪生网络(Siamese network)
- 匹配网络(Matching network)
- 原型网络(Prototypical Networks)
- 关系网络(Relation Network)
小样本学习记录————四种相似性计算经典网络结构
人类可以通过很少的样本就能学会分辨事务,所以使用较少的样本就可以训练得到一个有不错效果的模型,一直是机器学习特别期待实现的。在读小样本学习文章总会涉及以下几个经典的模型结构,在此进行一一总结。
孪生网络(Siamese network)
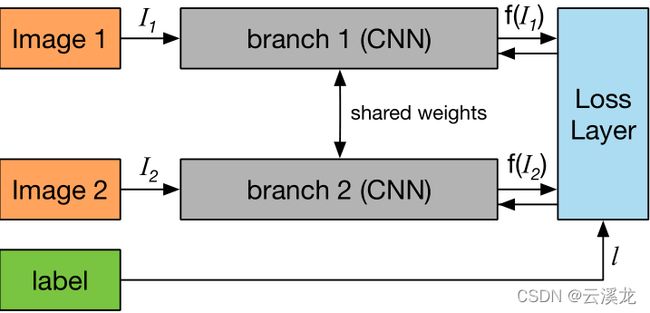
孪生网络在2015年被提出使用在one-shot识别中,一般是基于神经网络获得的特征向量,相似度用欧氏距离来度量。网络的结构很简单,如下图所示:通过共享权重的卷积网络(一般网络一致)得到输入图像的特征向量,通过最小化相同类别之间loss,最大化不同类别物体loss进行迭代训练得到一个可以判断两个物体是否相似的网络。
L = 1 2 l D 2 + 1 2 ( 1 − l ) { m a x ( 0 , m − D ) } 2 \mathcal L = \frac 1 2 lD^2 + \frac 1 2(1-l)\{max(0,m-D)\}^2 L=21lD2+21(1−l){max(0,m−D)}2
- l l l:如果 I 1 和 I 2 I_1和I_2 I1和I2相同类别为1,否则为0
- D D D:表示 I 1 和 I 2 I_1和I_2 I1和I2特征向量的欧式距离
- m m m:不相似向量之间最小的距离
在小样本学习中,查询集和支持集中图片进行比对得到相似度最高的图片,往往可以得到比较不错的结果。我们可以发现,如果进行多类别识别的问题中,这个比对过程效率比较低下,所以才有了后续的改进模型。
匹配网络(Matching network)
匹配网络在embedding得到特征向量后,通过引入注意力分析两者的相似性。在Matching networks for one shot learning文章中的注意力计算公式。
a ( x ^ , x i ) = e c f ( x ^ ) , g ( x i ) ∑ j = 1 k e c f ( x ^ ) , g ( x j ) a(\hat x,x_i)= \frac {e^{cf(\hat x),g(x_i)} } {\sum_{j=1}^k e^{cf(\hat x),g(x_j)}} a(x^,xi)=∑j=1kecf(x^),g(xj)ecf(x^),g(xi)
- x ^ \hat x x^是查询集
- x i x_i xi是支持集
- c表示计算两者的余弦距离
计算每一个余弦距离再进行softmax
模型最后的输出为是 y ^ \hat y y^为每一种标签的概率
P ( y ^ ∣ x ^ , S ) = ∑ i = 1 k a ( x ^ , x i ) y i P(\hat y|\hat x, S)=\sum_{i=1}^k a(\hat x,x_i)y_i P(y^∣x^,S)=i=1∑ka(x^,xi)yi
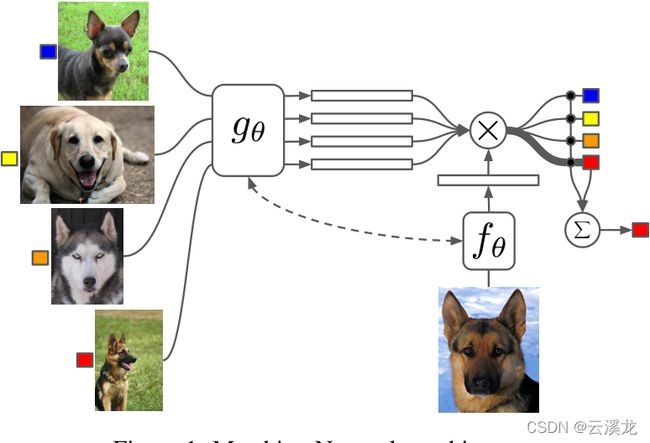
神经网络中的这样的非参数结构使得网络更容易记忆和适应同一任务中的新训练集,但是如果支持集的增多训练的代价就变大了,这是为什么后续又继续改进的原因之一。
如果对注意力机制不是很清楚可以看这篇文章注意力机制的基本思想和实现原理
原型网络(Prototypical Networks)
原型网络提出,先把样本投影到一个空间,计算每个样本类别的中心,在分类的时候,通过对比目标到每个中心的距离,从而分析出目标的类别。
c k = 1 ∣ S k ∣ ∑ ( x i , t i ) ∈ S k f ϕ ( x i ) c_k=\frac 1 {|S_k|} \sum_{(x_i,t_i)\in S_k }f_\phi(x_i) ck=∣Sk∣1(xi,ti)∈Sk∑fϕ(xi)
- c k c_k ck:表示k类样本的嵌入空间
- S k S_k Sk:表示标签为k的集合
- f ϕ f_\phi fϕ:表示一种embedding方式
可以理解为其实这就是一个算k类样本中心的函数
对于一个样本可以通过softmax它与每一类的距离,得到最有可能的类,公式如下。
P ( y = k ∣ x ) = e x p ( − d ( f ( x ) , c k ) ) ∑ k ′ e x p ( − d ( f ( x ) , c k ′ ) ) P(y=k|x)=\frac {exp(-d(f(x),c_k))} {\sum_{k'}exp(-d(f(x), c_{k'}))} P(y=k∣x)=∑k′exp(−d(f(x),ck′))exp(−d(f(x),ck))
关系网络(Relation Network)
不论是孪生网络,匹配网络,还是原型网络,在分析两个样本的时候都是通过embedding后的特征向量距离(比如欧氏距离)来反映,而关系网络则是通过构建神经网络来计算两个样本之间的距离从而分析匹配程度,关系网络可以看成提供了一个可学习的非线性分类器用于判断关系,而上述三个网络的距离只是一种线性的关系分类器。
样本j与类别i之间的关系可以用公式表示为
r i , j = g φ ( C ( f ϕ ( x i ) , f ϕ ( x j ) ) ) r_{i,j}=g_\varphi(C(f_\phi(x_i),f_\phi(x_j))) ri,j=gφ(C(fϕ(xi),fϕ(xj)))
- r i , j r_{i,j} ri,j:表示样本j与类别i的相关分数
- g φ g_\varphi gφ:表示相关性计算模型
- C C C:这里的C表示拼接操作,不是计算距离
- f ϕ f_\phi fϕ:表示一种embedding方式
在面对k-shot问题时,将同一类别特征向量按位求和,形成特征图,在进行后续操作。
L = ∑ i = 1 m ∑ j = 1 n ( r i , j − 1 ( y i = = y j ) ) 2 \mathcal L = \sum_{i=1}^m\sum_{j=1}^n(r_{i,j}-1(y_i==y_j))^2 L=i=1∑mj=1∑n(ri,j−1(yi==yj))2
关系网络的创新点就是提出用神经网络,而不是欧氏距离去计算两个特征变量之间的匹配程度。