【一起来刷题】基础排序问题之归并排序,链表操作问题之合并K个升序链表
本章收录于专栏:一起来刷题,持续更新中……
更多精彩文章,欢迎大家关注我,一起学习,一起进步~
本文介绍一下另一个重要的排序算法:归并排序。归并排序仍然是算法思想大于算法本身,很多题的解题思路,会用到归并的思想,比如本文将会将的一道经典题:23.合并K个升序链表
目录
一、归并排序基础
1、两个数的排序
2、两个数组的归并排序
3、一个数组的归并排序
4、python代码实现
二、归并排序实例——合并K个升序链表
一、归并排序基础
1、两个数的排序
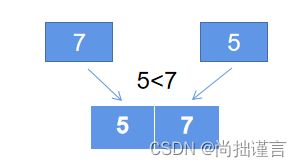
从最简单的开始,我们看下两个数咋排序,哈哈哈是不是很搞笑,不搞笑,合抱之木生于毫末~
我觉得我不用解释了,一张图就很清楚了~
2、两个数组的归并排序
如果是大于等于2个数进行排序,那可能就不止一两步啦~如下图示:
第一步:现分别将两个数组单独排序,让两个数组本身有序,这样图中所用的方法才能保证最终数组整体有序;
第二步:利用两个指针分别指向两个数组的头部(我们称后续指针指向的位置为数组的头部),并对比两个头部位置的数的大小,谁小取谁,小的一方,其指针向后移动一步,另一方指针不动;
第三步:继续对比两个指针指向位置的数的大小,谁小取谁,小的一方,其指针向后移动一步,另一方指针不动;
第四步、第五步继续上述过程,直到整个数组排序完毕。
3、一个数组的归并排序
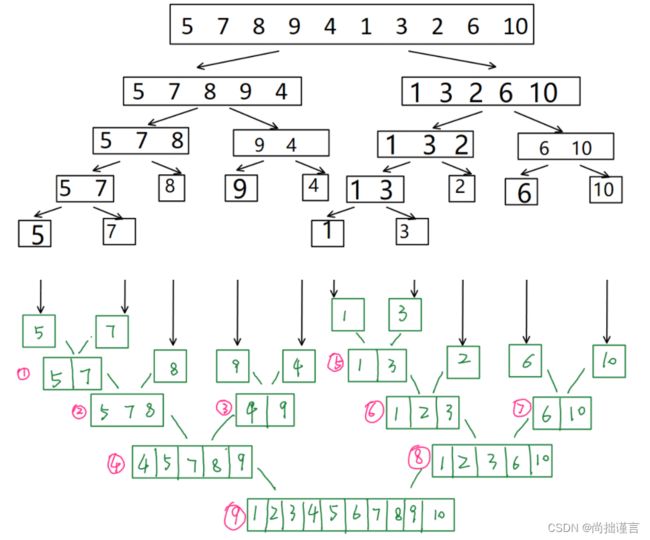
所谓道生一,一生二,对于一个数组的排序,我们完全可以将其劈开成两个数组进行上文两个数组排序的过程,我们注意看上文两个数组排序的第一步,其实是第1节中两个数的排序过程,很容易想到,如果不是2个单独数的排序,那么对于两个无序数组,按照对比头部大小的方法,最终也不能保证数组整体有序。这样一来,我们就要再分别将两个数组继续劈开,直到劈成单独的数,然后归并(归并:即进行上图中自顶向下的过程),归并的过程两两对比大小,最终合成一个数组使其整体有序。整个过程就是:先分开,再合并,合并的时候比大小。如下图示(图来源于网络):
上图的上半部分黑色的部分中,所有叶子节点的状态,其实就是第2节图例中的开始,下半部分绿色部分,其实就是第2节图例中自顶向下的过程。
4、python代码实现
from typing import List
class Solution:
def sortArray(self, nums: List[int]) -> List[int]:
if len(nums) == 1:
return nums
return self.mergeSort(nums)
# 归并排序
def mergeSort(self, arr):
if len(arr) == 1:
return arr
def merge(arr, left, mid, right):
"""
两个数组的排序
"""
p1, p2 = left, mid + 1
helper = []
# TODO 边界条件包括"="
while p1 <= mid and p2 <= right:
if arr[p1] < arr[p2]:
helper.append(arr[p1])
p1 += 1
else:
helper.append(arr[p2])
p2 += 1
while p1 <= mid:
helper.append(arr[p1])
p1 += 1
while p2 <= right:
helper.append(arr[p2])
p2 += 1
for i in range(len(helper)):
arr[left + i] = helper[i]
return arr
def sort(arr, left, right):
"""
劈数组以及归并的过程
"""
if left == right:
return
mid = left + ((right - left) >> 1)
# TODO 先sort再merge
# 先劈数组左半部分
sort(arr, left, mid)
# 再劈数组右半部分
sort(arr, mid + 1, right)
# 劈完后归并,归并过程中比大小进行排序
merge(arr, left, mid, right)
return arr
return sort(arr, 0, len(arr) - 1)
if __name__ == '__main__':
solution = Solution()
print(solution.sortArray([4,5,2,3,1]))由于每次我们只处理数组的一半的一半的一半的一半……,所以,归并的时间复杂度为O(NlogN) ,又因为我们在排序的过程中,借助了辅助数组helper,它的大小和数组的大小一样,存放排序后的数组,所以空间复杂度为O(N)。
二、归并排序实例——合并K个升序链表
- 先看下题目:
- 解题思路:
由于题目中每个链表已经是升序排列,所以对于数组中的链表来说,我们没有必要再劈开了,直接使用头部对比的方法即可。但是我们要对数组中所有的链表都进行排序操作,如果我们把每个链表看成一个数,其实问题就转化成了对一个数组进行排序了,所以我们要劈的是这个数组,而不是每个链表本身。又因为题目要求将所有链表合并成一个有序链表,所以不得不想到用归并的思想了。
首先,我们先搞定两个链表排序的问题:
def mergeTwolists(h1, h2):
head = ListNode(None)
p = head
while h1 and h2:
if h1.val < h2.val:
p.next = ListNode(h1.val)
h1 = h1.next
else:
p.next = ListNode(h2.val)
h2 = h2.next
p = p.next
if h1:
p.next = h1
if h2:
p.next = h2
return head.next其次,我们对数组进行开劈和归并,需要注意的是,分治到最后就是left==right,所以递归的终止条件为return arr[left],因此左部分和右部分的分治都需要返回分治后左部分和右部分的链表头,代表着即将合并的两个链表;递归函数返回的是合并两个链表的结果:
def merge(lists, left, right):
if left >= right:
# 容易错
return lists[left]
mid = left + ((right - left) >> 1)
# 容易漏掉l1和l2
l1 = merge(lists, left, mid)
l2 = merge(lists, mid + 1, right)
return mergeTwolists(l1, l2)- 整体代码:
from typing import List, Optional
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
class Solution:
def mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:
if not lists or (len(lists) == 1 and not lists[0]):
return None
def mergeTwolists(h1, h2):
head = ListNode(None)
p = head
while h1 and h2:
if h1.val < h2.val:
p.next = ListNode(h1.val)
h1 = h1.next
else:
p.next = ListNode(h2.val)
h2 = h2.next
p = p.next
if h1:
p.next = h1
if h2:
p.next = h2
return head.next
def merge(lists, left, right):
if left >= right:
# 容易错
return lists[left]
mid = left + ((right - left) >> 1)
# 容易漏掉l1和l2
l1 = merge(lists, left, mid)
l2 = merge(lists, mid + 1, right)
return mergeTwolists(l1, l2)
return merge(lists, 0, len(lists) - 1)参考文档:
归并排序图文详解_大家好,我是好同学的博客-CSDN博客_归并排序