C++实现查找 - 顺序、二分和哈希查找

数据结构与算法专栏 —— C++实现

写在前面：
前面我们其实已经涉及到了查找算法，比如二叉排序树和平衡二叉树等。这一讲我们来补充一下其它常见的查找算法，下面我会依次讲解并实现顺序查找、二分查找和哈希查找算法。

顺序查找

大家看到顺序查找可能第一时间会想到从前往后遍历，遇到与关键值相等的就输出其下标。这里我们来优化一下，让数组从下标为 1 的地方开始存储元素，然后将下标为 0 的地方放入查找关键值作为哨兵位。

这样的好处就是不用去担心数组越界的问题，当遍历到数组为 0 的时候说明就查找失败，并且直接返回 -1 即可。

#include 
using namespace std;

//顺序查找
int searchSeq(int *a, int len, int key) {
	a[0] = key;	//将下标为0的位置设置为哨兵位
	for (int i = len; i; i--)
		if (a[i] == a[0])
			return i;
	return -1;
}

int main() {
	int a[11] = {0, 5, 12, 16, 24, 33, 45, 56, 58, 68, 79};
	int key;
	cin >> key;
	int index = searchSeq(a, 10, key);
	if (index == -1)
		cout << "没有该元素！" << endl;
	else
		cout << index << endl;
	return 0;
}

二分查找

二分查找正如其名，我们将区间分成两半进行查找：

1. 首先初始化左边界和右边界。
2. 每次都取当前区间的中间位置，用于判断。
   1. 如果中间值等于查找的关键值，则返回当前中间位置下标。
   2. 如果中间值小于查找的关键值，则说明关键值在左半区间，r = mid - 1 。
   3. 如果中间值大于查找的关键值，则说明关键值在右半区间，l = mid + 1 。
3. 如果没找到则直接返回 -1 。

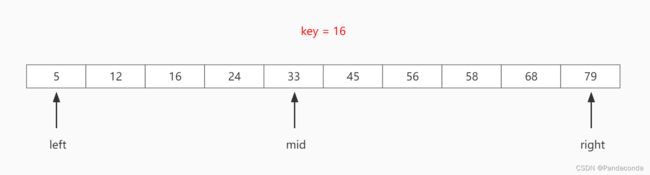
我们直接上图来理解：

第一步：初始化指针，并得到 mid = left + right >> 1 ，即 mid = 4 。（这里的 >> 1 相当于除以 2 的效果）

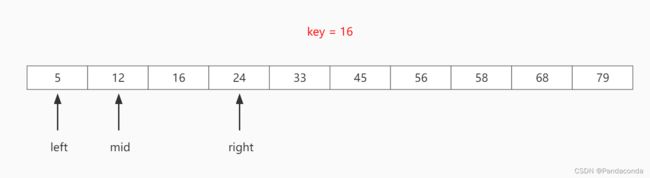
第二步：发现 key < mid 指向的值，故将 right = mid - 1 ，再次计算 mid 位置。

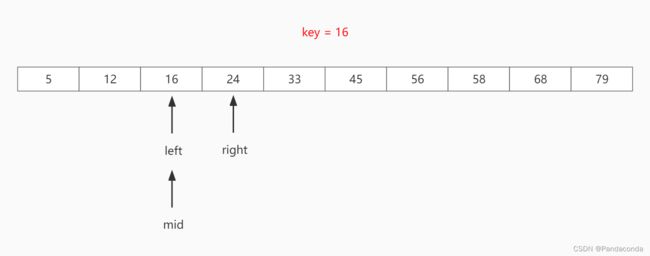
第三步：发现 key > mid 指向的值，故将 left = mid +1 ，再次计算 mid 位置。此时 mid 指向的值等于 key ，故直接输出当前所指下标。

#include 
using namespace std;

//二分查找
int binarySearch(int *a, int len, int key) {
	int left = 0, right = len - 1;
	while (left <= right) {
		int mid = left + right >> 1;	//去区间中间位置
		if (key == a[mid])	//如果找到关键值就返回当前下标
			return mid;
		else if (key < a[mid])	//如果关键值小于中间值说明其在左半边区间
			right = mid - 1;
		else	//否则关键值在右半边区间
			left = mid + 1;
	}
	return -1;
}

int main() {
	int a[10] = {5, 12, 16, 24, 33, 45, 56, 58, 68, 79};
	int key;
	cin >> key;
	int index = binarySearch(a, 10, key);
	if (index == -1)
		cout << "没有该元素！" << endl;
	else
		cout << index + 1 << endl;
	return 0;
}

哈希查找

何为哈希，通俗来讲就是将关键值利用具体的哈希函数来映射到数组中的某个位置。这样我们就可以通过 O(1) 的时间复杂度来找到要查找的关键值。

那么问题来了，数组就那么大，如果出现映射位置相同的关键值该怎么办。下面我将介绍三种解决方法，分别是链地址法、线性探测再散列法和二次探测再散列法。其中重点关注前两个算法，二次探测再散列法稍微没有那么重要，但我还是会进行讲解。

链地址法

既然关键值映射时会发生冲突，我们干脆可以利用一个链表，将冲突的关键值串成一条放在对应区域。我们还是直接上图来理解：

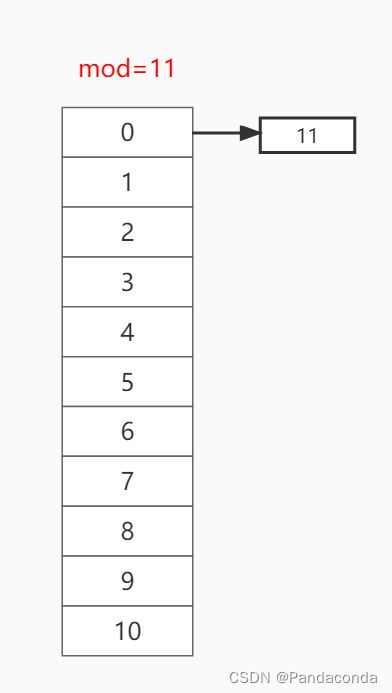
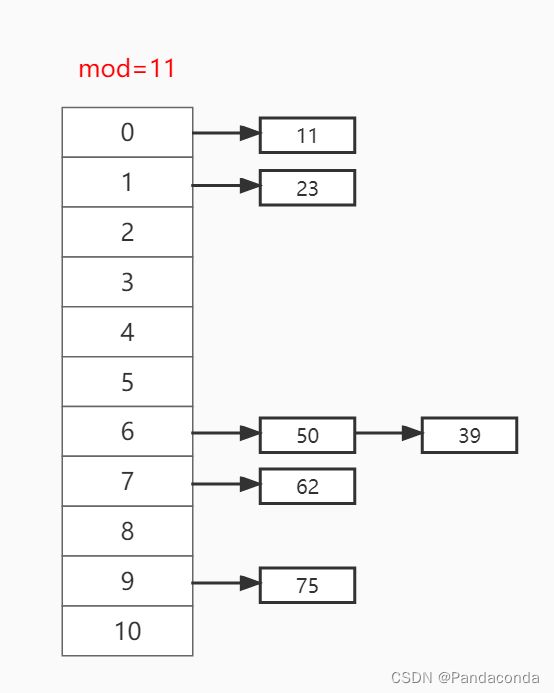
假设我们初始数组为 { 11 , 23 , 39 , 50 , 75 , 62 } ，并且模数为 11 ，我们先进行插入的操作。

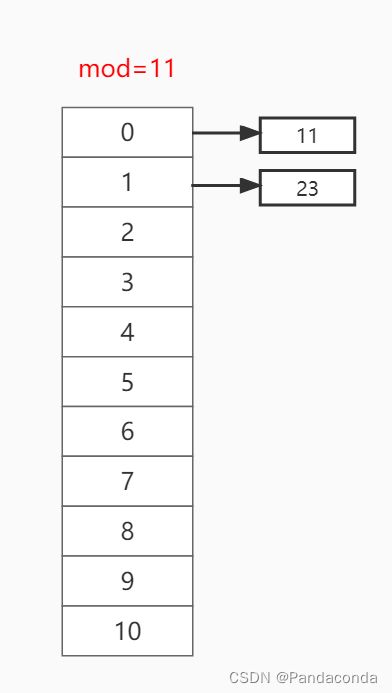
第一步：插入关键值 11 ，放入哈希函数取模 11 % 11 = 0 ，故放到下标为 0 的位置。

第二步：插入关键值 23 ，放入哈希函数取模 23 % 11 = 1 ，故放到下标为 1 的位置。

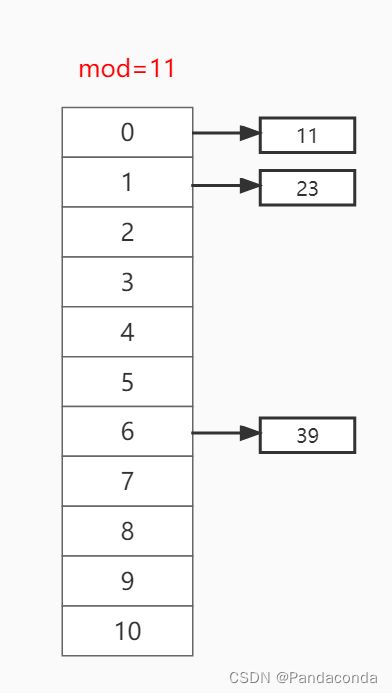
第三步：插入关键值 39 ，放入哈希函数取模 39 % 11 = 6 ，故放到下标为 6 的位置。

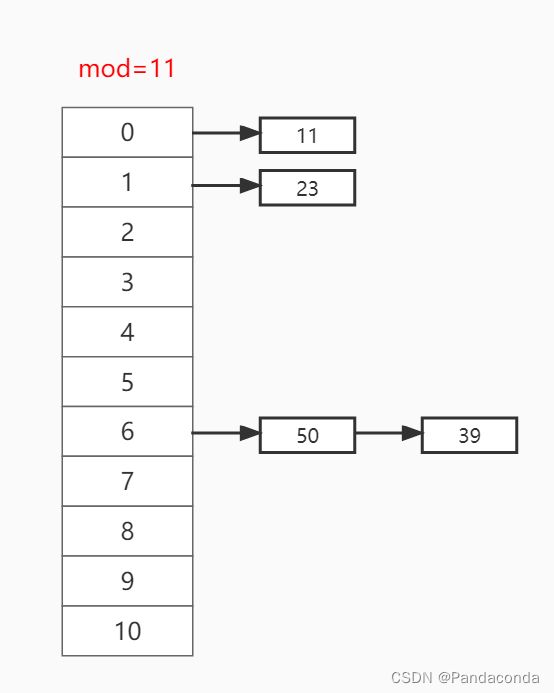
第四步：插入关键值 50 ，放入哈希函数取模 50 % 11 = 6 ，故放到下标为 6 的位置。但是该位置已经放有元素，所以我们直接用链表将他们串起来，这里采用头插法。

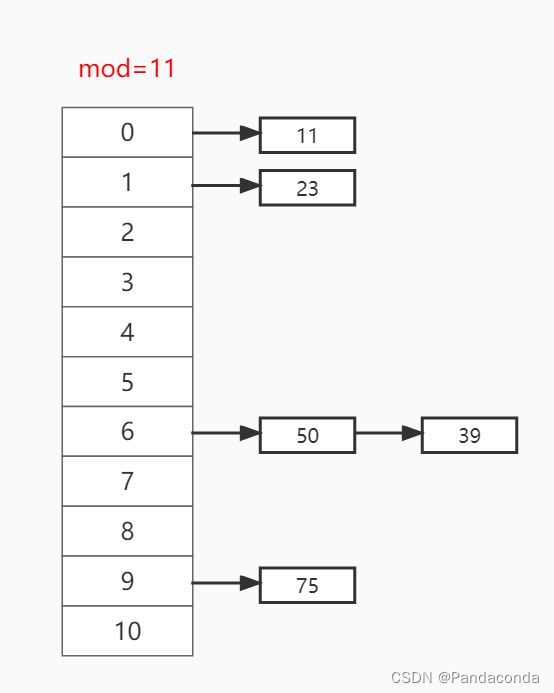
第五步：插入关键值 75 ，放入哈希函数取模 75 % 11 = 9 ，故放到下标为 9 的位置。

第六步：插入关键值 62 ，放入哈希函数取模 62 % 11 = 7 ，故放到下标为 7 的位置。但是该位置已经放有元素，同样采用头插法插入。

至于查找操作就十分简单了，我们还是举几个例子。

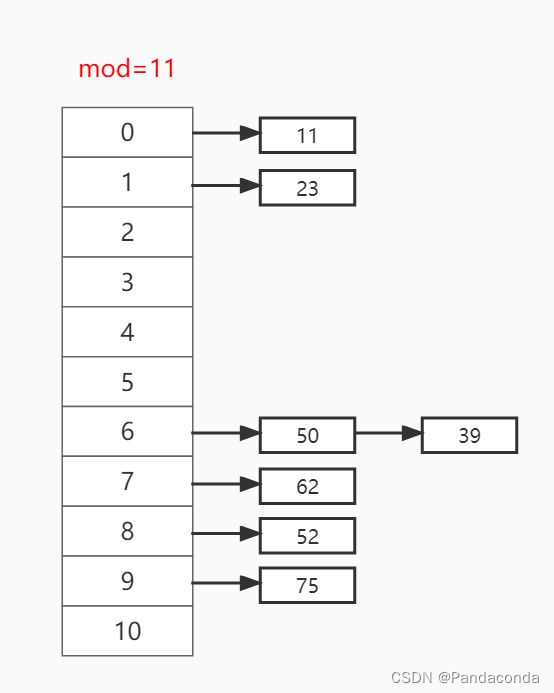
第七步：查找关键值 39 ，放入哈希函数取模 39 % 11 = 6 ，找到下标为 6 的位置。发现不止一个值，则进行遍历，发现该值存在，故直接返回。

第八步：查找关键值 52 ，放入哈希函数取模 52 % 11 = 8 ，找到下标为 8 的位置。发现没有元素，所以该值不存在，则进行插入操作。

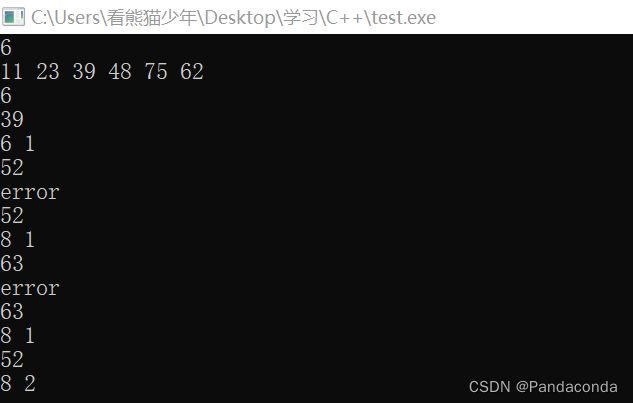
这里我们代码的实现是遵循上面提到的原则，假设模数为 11 。遇到冲突的关键值采用头插法，并且如果找到关键值就返回所在下标和查找的次数，否则就插入该关键值。

#include 
using namespace std;

/*
6
11 23 39 48 75 62
6
39
52
52
63
63
52
*/

int mod = 11;	//假设模数为 11

//定义结点
struct Node {
	int data;
	Node *next;
};

//哈希插入
void hash_insert(vector<Node *> arr, int x) {
	int dis = x % mod;
	Node *node = new Node;
	node->data = x;
	node->next = arr[dis]->next;	//采用头插法插入元素
	arr[dis]->next = node;
}

//哈希查找
bool hash_find(vector<Node *> arr, int x) {
	int dis = x % mod;
	Node *temp = arr[dis]->next;
	int cnt = 0;	//记录查找的次数
	//查找该区域的所有元素
	while (temp != NULL) {
		cnt++;
		if (temp->data == x) {
			//输出元素位置以及查找的次数
			cout << dis << " " << cnt << endl;
			return true;
		}
		temp = temp->next;
	}
	cout << "error" << endl;
	return false;
}

int main() {
	int n, t;	//元素个数和查找元素的次数
	while (cin >> n) {
		vector<Node *> arr(12);
		//初始化
		for (int i = 0; i < 11; i++) {
			Node *node = new Node;
			node->data = INT_MAX;
			node->next = NULL;
			arr[i] = node;
		}
		//插入操作
		for (int i = 0; i < n; i++) {
			int x;
			cin >> x;
			hash_insert(arr, x);
		}
		//查找操作
		cin >> t;
		while (t--) {
			int x;
			cin >> x;
			bool flag = hash_find(arr, x);
			//如果找不到就插入该值
			if (flag == false)
				hash_insert(arr, x);
		}
	}
}

线性探测再散列法

这里讲的线性探测再散列法和二次探测再散列法其实都可以归于开放定址法，开放地址法包含很多方法，但是我们这里只讲最常见的两个。

我们的开放定址法都可以遵循以下公式：

H₀= H(key)，一般就是取模
H_i = ( H(key) + d_i ) mod m, i = 1, 2, …, s
这里的 d_i 取决于我们用的方法，并且其值不可以超过哈希表长 m 。另外，H_i 中加完 d_i 模的是 m 即哈希表长。

一开始看这些公式可能会比较懵，我们还是带入例子来给大家讲解。

我们先来看线性探测再散列法，当插入的关键值冲突时就需要用到上面的公式。而这种方法就是在关键值每次冲突时都加上一个数值 d_i ，这个 d_i 在遇到连续冲突时会递增。

也就是说 d_i 满足如下规则：

d_i = c∙ i（一般取 c = 1）, 1 ≤ i ≤ m - 1，如 1, 2, 3 …

同样，直接上图理解：

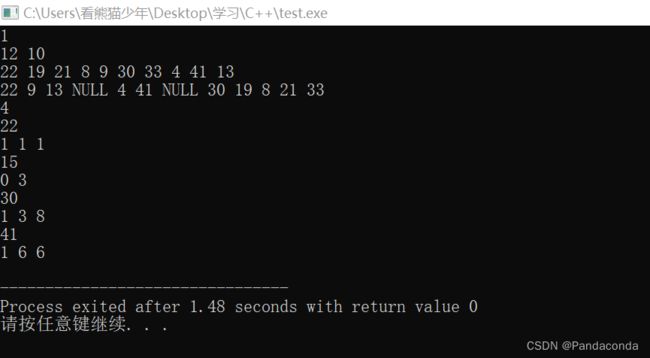
假设我们的初始数组为 { 22 , 19 , 21 , 8 , 9 , 30 , 33 , 4 , 15 , 14 }，模数还是 11 ，并且哈希表表长为 12 。可能会有小伙伴比较疑惑，为什么表长会比模数还要大，因为我们上面提到 H_i 函数最终模的是表长，所以和哈希函数 H₀ 中的模数没有任何关系。

我们还是先来看插入操作。

第一步：插入关键值 22 ，放入哈希函数取模 22 % 11 = 0 ，故放到下标为 0 的位置。

第二步：插入关键值 19 ，放入哈希函数取模 19 % 11 = 8 ，故放到下标为 8 的位置。

第三步：插入关键值 21 ，放入哈希函数取模 21 % 11 = 10 ，故放到下标为 10 的位置。

第四步：插入关键值 8 ，放入哈希函数取模 8 % 11 = 8 ，故放到下标为 8 的位置。但是该位置已经放有元素，所以调用上面的函数，第一次发生冲突， d_i 为 1 。8 + 1 = 9 % 12 = 9 ，故放到下标为 9 的位置。

第五步：插入关键值 9 ，放入哈希函数取模 9 % 11 = 9 ，故放到下标为 9 的位置。但是该位置已经放有元素，所以调用上面的函数，第一次发生冲突， d_i 为 1 。9 + 1 = 10 % 12 = 10 ，故放到下标为 10 的位置。

但是下标为 10 的位置也放有元素，故继续调用上面的函数，此时是第二次发生冲突，d_i 加 1 等于 2 。9 + 2 = 11 % 12 = 11 ，故放到下标为 11 的位置。注意这里并不是用上面的得到的 10 继续加，而是用原来的哈希值来加即 H₀ 。

第六步：插入关键值 30 ，放入哈希函数取模 30 % 11 = 8 ，故放到下标为 8 的位置。但是该位置已经放有元素，所以按照上述步骤，得到最终位置 2 。

第七步：插入关键值 33 ，放入哈希函数取模 33 % 11 = 0 ，故放到下标为 0 的位置。但是该位置已经放有元素，所以按照上述步骤，得到最终位置 3 。

第八步：插入关键值 4 ，放入哈希函数取模 4 % 11 = 4 ，故放到下标为 4 的位置。

第九步：插入关键值 15 ，放入哈希函数取模 15 % 11 = 4 ，故放到下标为 4 的位置。但是该位置已经放有元素，所以按照上述步骤，得到最终位置 5 。

第十步：插入关键值 14 ，放入哈希函数取模 14 % 11 = 3 ，故放到下标为 3 的位置。

#include 
using namespace std;

/*
1
12 10
22 19 21 8 9 30 33 4 15 14
4
22
56
30
17
*/

int mod = 11;	//模数
int m;	//表长

//哈希查找
bool hash_find(int *arr, int dis) {
	if (arr[dis] == 0x3f3f3f3f)
		return true;
	return false;
}

//哈希插入
int hash_search(int *arr, int x) {
	int k = 0;	//设置累加值
	int dis = x % mod;
	while (k <= m - 1) {
		k++;	//每次查找都会加1（连续冲突）
		bool flag = hash_find(arr, dis);	//判断该值是否在哈希表中
		//如果查找位置为空，则说明该位置可以插入元素
		if (flag == true)
			return dis;
		dis = (x % mod + k) % m;	//重新计算哈希值
	}
	return -1;
}

//这里另外写一个哈希查找用于专门的查找操作，因为查找和插入对于arr数组的判断条件不同
int cnt;	//计算查找次数
int search(int *arr, int x) {
	int k = 0;
	int dis = x % mod;
	//k值不能超过表长
	while (k <= m - 1) {
		k++;
		cnt++;
		//如果查找位置等于关键值则返回下标
		if (arr[dis] == x)
			return dis;
		else if (arr[dis] == 0x3f3f3f3f)
			return -1;
		dis = (x % mod + k) % m;	//重新计算哈希值
	}
	return -1;
}

int main() {
	int n, t, k;
	cin >> t ;
	while (t--) {
		cin >> m >> n;
		int *arr = new int[m];
		//初始化哈希数组，将数组值初始化为非常大的值
		for (int i = 0; i < m; i++)
			arr[i] = 0x3f3f3f3f;
		//插入操作
		for (int i = 0; i < n; i++) {
			int x;
			cin >> x;
			int dis = hash_search(arr, x);
			arr[dis] = x;
		}
		//输出散列表
		for (int i = 0; i < m; i++) {
			//如果当前位置为超大值，说明为空，还未插入元素
			if (arr[i] != 0x3f3f3f3f)
				cout << arr[i] << " ";
			else
				cout << "NULL ";
		}
		cout << endl;
		//查找操作
		cin >> k;
		while (k--) {
			int x;
			cin >> x;
			cnt = 0;
			int dis = search(arr, x);
			//如果找不到就直接输出查找次数，否则输出查找次数和在数组中第几个位置
			if (dis == -1)	//查找不成功输出0
				cout << 0 << " " << cnt << endl;
			else	//否则输出1
				cout << 1 << " " << cnt << " " << dis + 1 << endl;
		}
	}
	return 0;
}

二次探测再散列法

二次探测再散列和线性探测再散列十分相像，只是 d_i 的计算不同，其它公式都一样。

d_i = (-1)ⁱ⁺¹ ( (i+1) / 2)², 1 ≤ i ≤ m/2 ，如 1² ,-1² ,2² ,-2² …

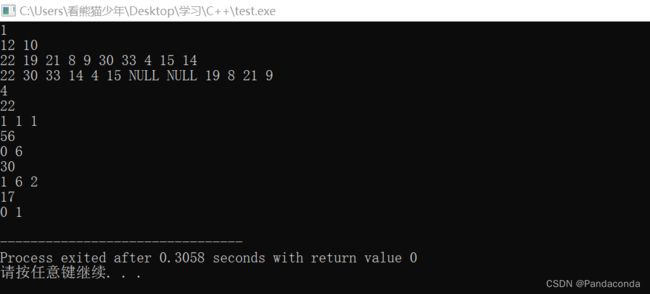
由于代码十分相近，这里就不再进行画图讲解了，直接来看代码~

#include 
using namespace std;

/*
1
12 10
22 19 21 8 9 30 33 4 41 13
4
22
15
30
41
*/

int mod = 11;	//模数
int m;	//表长

//哈希查找
bool hash_find(int *arr, int dis) {
	if (arr[dis] == 0x3f3f3f3f)
		return true;
	return false;
}

//哈希插入
int hash_search(int *arr, int x) {
	int k = 0;
	int dis = x % mod;
	while (k <= m / 2) {
		k++;
		if (arr[dis] == x)
			return -1;
		bool flag = hash_find(arr, dis);
		if (flag == true)
			return dis;
		//重新计算哈希函数
		int temp = pow(-1, k + 1);
		dis = (x % mod + temp * ((k + 1) / 2) * ((k + 1) / 2)) % m;
		while (dis < 0)
			dis += m;
	}
	return -1;
}

//同样用两个函数一个用于插入一个用于查找
int cnt;
int search(int *arr, int x) {
	int k = 0;
	int dis = x % mod;
	while (k <= m - 1) {
		k++;
		cnt++;
		if (arr[dis] == x)
			return dis;
		else if (arr[dis] == 0x3f3f3f3f)
			return -1;
		//重新计算哈希值
		int temp = pow(-1, k + 1);
		dis = (x % mod + temp * ((k + 1) / 2) * ((k + 1) / 2)) % m;
		while (dis < 0)
			dis += m;
	}
	return -1;
}

int main() {
	int n, t, k;
	cin >> t;
	while (t--) {
		cin >> m >> n;
		int *arr = new int[m];
		for (int i = 0; i < m; i++)
			arr[i] = 0x3f3f3f3f;
		//插入操作
		for (int i = 0; i < n; i++) {
			int x;
			cin >> x;
			int dis = hash_search(arr, x);
			arr[dis] = x;
		}
		//输出散列表
		if (arr[0] != 0x3f3f3f3f)
			cout << arr[0];
		else
			cout << "NULL";
		for (int i = 1; i < m; i++) {
			if (arr[i] != 0x3f3f3f3f)
				cout << " " << arr[i];
			else
				cout << " NULL";
		}
		cout << endl;
		//查找操作
		cin >> k;
		while (k--) {
			int x;
			cin >> x;
			cnt = 0;
			int dis = search(arr, x);
			if (dis == -1)
				cout << 0 << " " << cnt << endl;
			else
				cout << 1 << " " << cnt << " " << dis + 1 << endl;
		}
	}
	return 0;
}

如果大家有什么问题的话，欢迎在下方评论区进行讨论哦~