人工智能 对比试验_人工智能实验三：分类算法实验

一、实验目的

1、巩固4种基本的分类算法的算法思想：朴素贝叶斯算法，决策树算法，人工神经网络，支持向量机算法；

2、能够使用现有的分类器算法代码进行分类操作；

3、学习如何调节算法的参数以提高分类性能；

二、实验硬件软件平台

硬件：计算机

软件：操作系统：WINDOWS

应用软件：C，Java或者Matlab、Weka

三、实验内容

利用现有的分类器算法对文本数据集进行分类

实验步骤：

1．了解文本数据集的情况并阅读算法代码说明文档；

2．利用文本数据集中的训练数据对算法进行参数学习；

3．利用学习的分类器对测试数据集进行测试；

4．统计测试结果；

软件下载与安装；实验资料下载

软件使用weka3.8，下载链接：https://sourceforge.net/projects/weka/，可以直接使用。

实验资源下载：https://pan.baidu.com/s/1PqxBDF4pjcV1F63PXYJIOw 密码：r54q

包含实验算法的原理讲解和arff格式的数据集。

实验过程操作及现象

1、数据集的获取及格式转换

1.1TXT文本转换为CSV

Excel的XLS文件可以让多个二维表格放到不同的工作表(Sheet)中，我们只能把每个工作表存成不同的CSV文件。打开一个XLS文件并切换到需要转换的工作表，另存为CSV类型，点“确定”、“是”忽略提示即可完成操作。

本次实验中提供的数据集data set是用逗号分隔的，可以使用Excel中的“导入数据”功能，最后另存为CSV。

1.2CSV转换为arff

将CSV转换为ARFF最迅捷的办法是使用WEKA本身。

在Explorer界面选择open file，然后打开CSV文件，选择save，保存格式选择arff，之后再点击open file打开arff文件即可。

WEKA存储数据的格式是ARFF(Attribute-Relation File Format)文件，这是一种ASCII文本文件。它包含关系声明和属性声明。

2、Weka的使用

如图是进入软件的界面，点击explorer，我们实验的功能都在那个里面。

点击open file，选择第一步中转换好的.arff格式的数据集导入，待界面上可以看到数据之后，点击右边的“Classify”，进行分类算法的测试。

点击choose按钮，选择需要测试的算法，在test_options中选择算法的参数，在下拉列表中选择分类的关键依据参数，点击start即可完成分类的测试。

3、各算法的测试

3.1：分类关键依据的选定

在导入好dataset之后，点击weka界面的最上面最右边的visualize，即可进入数据可视化界面，此时可以生成一张如上图所示的数据分布情况图(设定plotsize=100，pointsize和jitter向右拉满)，点击Update。

【注意，实验里面有三个数据集，建议使用dataset(总数据集)，test(训练集)，predict(测试集)】

这个地方观察数据的总体分布状况，故用最全的dataset。

观察图片，发现除了第一行的class values各个颜色的圈之间位置分布有较大差别，而其他属性，各个颜色的圈分布位置差别不大，因此，我们选用class values作为分类的依据，效果会比使用其他属性要好。

3.2：分类及测试方法

使用test作为数据集，共1349组数据；使用predict作为测试集，共377组数据。

算法的选定、具体参数设置请看图。

3.3：朴素贝叶斯

训练过程：【点击Use traning set，注意导入的数据为test而非dataset】

如果使用了dataset作为训练集，那么由于测试集predict也被包含在dataset这个总数据集里，测试出来的结果会正确率很高，但是也失去了意义，因为是自己测试自己。(之后的算法也是一样的)

Correctly Classified Instances 1191 88.2876 %

Incorrectly Classified Instances 158 11.7124 %

Kappa statistic 0.6888

Mean absolute error 0.0993

Root mean squared error 0.2053

Relative absolute error 48.4529 %

Root relative squared error 64.2275 %

Total Number of Instances 1349

训练集分类正确率为88.2876%。

测试过程：【测试集选定的时候，需要点击左边的Supplied test set右边的set按钮，选定predict为测试集，之后的算法相同】

Correctly Classified Instances 259 68.7003 %

Incorrectly Classified Instances 118 31.2997 %

Kappa statistic 0.4326

Mean absolute error 0.1631

Root mean squared error 0.3224

Relative absolute error 62.0086 %

Root relative squared error 80.52%

Total Number of Instances 377

经过测试，得出朴素贝叶斯的正确率为68.7003%。

3.4：决策树

训练过程：

Correctly Classified Instances 1304 96.6642 %

Incorrectly Classified Instances 45 3.3358 %

Kappa statistic 0.9189

Mean absolute error 0.026

Root mean squared error 0.1139

Relative absolute error 12.673 %

Root relative squared error 35.643 %

Total Number of Instances 1349

决策树分类正确率为96.6642%。

测试过程：

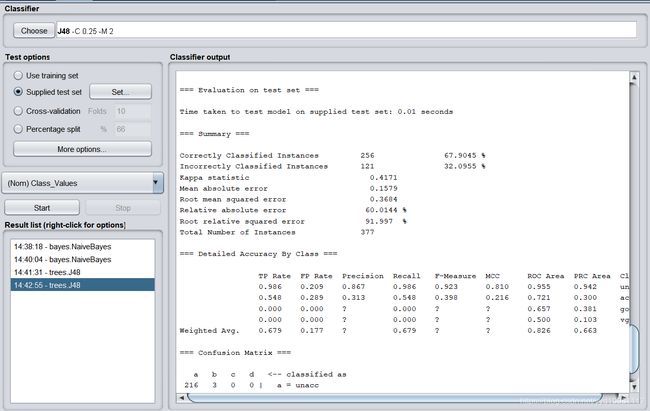
Correctly Classified Instances 256 67.9045 %

Incorrectly Classified Instances 121 32.0955 %

Kappa statistic 0.4171

Mean absolute error 0.1579

Root mean squared error 0.3684

Relative absolute error 60.0144%

Root relative squared error 91.997%

Total Number of Instances 377

使用测试集，得出决策树的分类结果正确率为67.9045%。

3.5：人工神经网络

训练过程：

Correctly Classified Instances 1349 100%

Incorrectly Classified Instances 0 0%

Kappa statistic 1

Mean absolute error 0.0018

Root mean squared error 0.0059

Relative absolute error 0.8944 %

Root relative squared error 1.8382 %

Total Number of Instances 1349

使用人工神经网络算法，训练集上的分类正确率可以达到100%。

测试过程：

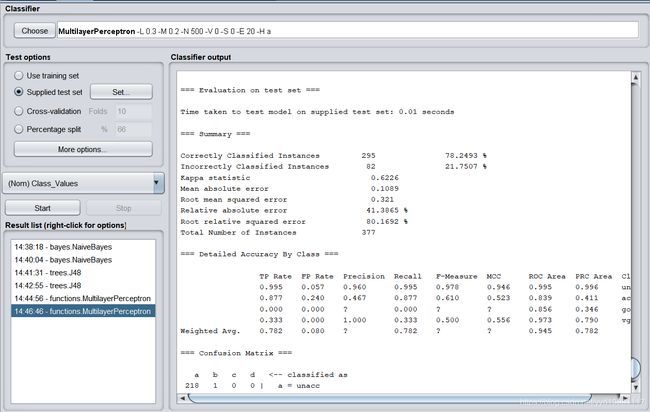
Correctly Classified Instances 295 78.2493 %

Incorrectly Classified Instances 82 21.7507 %

Kappa statistic 0.6226

Mean absolute error 0.1089

Root mean squared error 0.321

Relative absolute error 41.3865 %

Root relative squared error 80.1692 %

Total Number of Instances 377

使用人工神经网络，测试正确率达到了78.2493%。

3.6：支持向量机

训练过程：

Correctly Classified Instances 1282 95.0334 %

Incorrectly Classified Instances 67 4.9666 %

Kappa statistic 0.8795

Mean absolute error 0.2543

Root mean squared error 0.3185

Relative absolute error 124.1183 %

Root relative squared error 99.6308 %

Total Number of Instances 1349

支持向量机的分类正确率为95.1389%。

测试过程：

Correctly Classified Instances 280 74.2706 %

Incorrectly Classified Instances 97 25.7294 %

Kappa statistic 0.5559

Mean absolute error 0.2851

Root mean squared error 0.3618

Relative absolute error 108.4062 %

Root relative squared error 90.348 %

Total Number of Instances 377

支持向量机算法的测试正确率为74.2706%。

4、各算法原理(详细内容见上文链接中文档)

这里就简单写一点介绍吧。。

朴素贝叶斯

朴素贝叶斯分类是一种十分简单的分类算法，叫它朴素贝叶斯分类是因为这种方法的思想真的很朴素，朴素贝叶斯的思想基础是这样的：对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类项属于哪个类别。我们会选择条件概率最大的类别，这就是朴素贝叶斯的思想基础。

整个朴素贝叶斯分类分为三个阶段：

第一阶段——准备工作阶段，这个阶段的任务是为朴素贝叶斯分类做必要的准备，主要工作是根据具体情况确定特征属性，并对每个特征属性进行适当划分，然后由人工对一部分待分类项进行分类，形成训练样本集合。这一阶段的输入是所有待分类数据，输出是特征属性和训练样本。这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段，其质量对整个过程将有重要影响，分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。

第二阶段——分类器训练阶段，这个阶段的任务就是生成分类器，主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率估计，并将结果记录。其输入是特征属性和训练样本，输出是分类器。这一阶段是机械性阶段，根据前面讨论的公式可以由程序自动计算完成。

第三阶段——应用阶段。这个阶段的任务是使用分类器对待分类项进行分类，其输入是分类器和待分类项，输出是待分类项与类别的映射关系。这一阶段也是机械性阶段，由程序完成。

决策树

决策树(decision tree)是一个树结构(可以是二叉树或非二叉树)。其每个非叶节点表示一个特征属性上的测试，每个分支代表这个特征属性在某个值域上的输出，而每个叶节点存放一个类别。使用决策树进行决策的过程就是从根节点开始，测试待分类项中相应的特征属性，并按照其值选择输出分支，直到到达叶子节点，将叶子节点存放的类别作为决策结果。

不同于贝叶斯算法，决策树的构造过程不依赖领域知识，它使用属性选择度量来选择将元组最好地划分成不同的类的属性。所谓决策树的构造就是进行属性选择度量确定各个特征属性之间的拓扑结构。

ID3算法被用于选择属性度量。

人工神经网络

利用输出后的误差来估计输出层前一层的误差，再用这层误差来估计更前一层误差，如此获取所有各层误差估计。这里的误差估计可以理解为某种偏导数，我们就是根据这种偏导数来调整各层的连接权值，再用调整后的连接权值重新计算输出误差。直到输出的误差达到符合的要求或者迭代次数溢出设定值。

说来说去，“误差”这个词说的很多嘛，说明这个算法是不是跟误差有很大的关系？

没错，BP的传播对象就是“误差”，传播目的就是得到所有层的估计误差。

它的学习规则是：使用最速下降法，通过反向传播(就是一层一层往前传)不断调整网络的权值和阈值，最后使全局误差系数最小。

它的学习本质就是：对各连接权值的动态调整。

支持向量机

支持向量机(Support Vector Machine ,SVM)的主要思想是：建立一个最优决策超平面，使得该平面两侧距离该平面最近的两类样本之间的距离最大化，从而对分类问题提供良好的泛化能力。对于一个多维的样本集，系统随机产生一个超平面并不断移动，对样本进行分类，直到训练样本中属于不同类别的样本点正好位于该超平面的两侧，满足该条件的超平面可能有很多个，SVM正式在保证分类精度的同时，寻找到这样一个超平面，使得超平面两侧的空白区域最大化，从而实现对线性可分样本的最优分类。

5、思考题：如何在参数学习或者其他方面提高算法的分类性能？

以人工神经网络算法为例，调整学习相关参数，可以观察到如下结果。

以上是设置学习时间为300的情况，可以看到均方根误差为0.0096，训练时间2.41秒。

均方根误差是观测值与真值偏差的平方与观测次数n比值的平方根，在实际测量中，观测次数n总是有限的，真值只能用最可信赖(最佳)值来代替。对一组测量中的特大或特小误差反映非常敏感，所以，标准误差能够很好地反映出测量的精密度。因此这里我们使用均方差观察学习的准确性。

以上是设置学习时间为1300的情况，可以看到均方根误差为0.0044，训练时间10.32秒。

通过上述对比可以发现，训练时间越长，训练结果越准确，误差越低。这是因为随着训练时间的加长，迭代次数会越来越多，因此更容易接近实际准确情况。

下面，我们研究比对学习率对于均方根误差的影响：

以上是设置学习率为0.3的情况，训练时间设置为500，可以看到均方根误差为0.0073，实际训练时间为3.99秒。

此时我们将学习率设置为0.6，发现均方根误差降低到了0.0051，同时实际训练时间略有提升，达到了4.26秒，但是，此时我们人为所设定的学习时间并没有变化，此时我认为这里的时间提升，大致可以归因为一个可以被允许的误差。

而一味提升学习率就一定能够提升算法准确率吗？答案是否定的。因为学习率，又被成为“步长”。“步长”越大，每一次修改分类算法的关键参数的时候，这些参数的摆动幅度也就越大，因此，误差有可能随着学习率的提升而提升，而更为糟糕的是，学习率(步长)若过大，会使得算法在最优解附近不断来回摆动，因为步长太大的原因，算法参数无法收敛到全局最优，能否实际提升学习率是不确定的，全靠运气。

综上所述，我认为提高算法性能主要有两个方面：如果只需要提高运行速度，可以降低迭代次数，但这样会导致模型的误差增大；如果需要提高模型的精确度，就需要适当更改学习率，且一定要增加迭代次数，但是如果是通过增加迭代次数的方法提升精确度，那么相应的算法时间开销就会不可避免地增大。因此，从参数的角度来考虑分类器的学习建模，我们需要权衡精确度和效率之间的关系。