显示网格_Grasshopper网格基础应用

网格是3D建模领域最有代表性的几何形式，很多软件的构架都是以网格为中心，但是由于Rhino主要是针对Nurbs的操作，导致网格在Rhino以及GH中的操作容易被人忽视。网格与Nurbs的作用是互补的，很多Nurbs难以实现的模型都可以通过网格制作出来。

网格创建的模型与其他软件有较好的对接性，因为其在保存成3ds或者Obj格式后导入其他软件时，网格的拓扑关系不会发生变化，可继续对模型进行编辑。但是Nurbs模型在导入到其他软件过程中，往往需要先转换为网格，其拓扑结构往往与预期效果不一致，导致后面的软件没法对其进行有效的编辑，相信经常使用Sketch Up与Rhino进行模型互导的读者会深有感触。

网格可以大大提升模型的显示效率，因为计算机的显卡无法直接读取Nurbs物体，需要先在后台将其转换成网格才可以读取出来。如果模型本身就是网格的话，那么就无需这个转换过程，大大节约显示的计算时间。网格还可以通过Join的方法减少模型所占的存储空间，同样可以提升模型的显示效率。

由于GH中的Mesh命令相对较少且不够完善，因此需要外部插件来弥补其功能的缺失，较为常用的Mesh插件包含Mesh Edit、Weaverbird、Starling、Meshtools等。

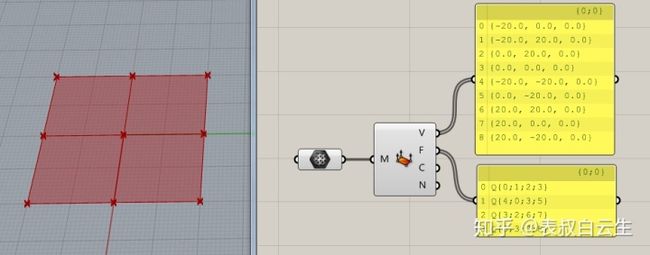
对于网格的含义，在Rhino中建立一个网格，然后用“What”命令查看对于网格的描述，可以发现该网格是由9个顶点，4个有法线的网格面组成。

将上面绘制的网格用Mesh运算器拾取进GH中，并用Deconstruct Mesh运算器将这个网格进行分解，其V输出端表示网格的顶点；F输出端表示的是每个网格面的顶点序号，用Panel面板查看其输出结果，其中Q表示的是Quad的含义，即为四边的Face，如果将三边网格面进行分解，输出端F中的数据则会显示T，所表示的即是Triangle的含义；输出端C表示的是顶点的颜色；输出端N表示的是顶点法线方向。

网格由Vertices、Edges、Faces共同组成，包含三边网格和四边网格。通过指定网格内部的拓扑关系（Topology），可以创建不同结构的网格。Construct Mesh运算器是创建网格的常用命令，需要确定网格的顶点以及网格面（Face），这里的网格面指的其实是顶点的排列序号，创建网格面可以通过在Panel面板中输入顶点序号，也可通过Mesh Quad以及Mesh Triangle运算器创建四边和三边的网格面。

在创建Mesh Faces的时候要尤其注意顶点序号的排列，只有正确的顶点排序才能生成正确的Mesh结果，如果顶点的排序是错误的，那么会生成有破面的网格，这样的模型在渲染或3D打印的情况下是会出错的。

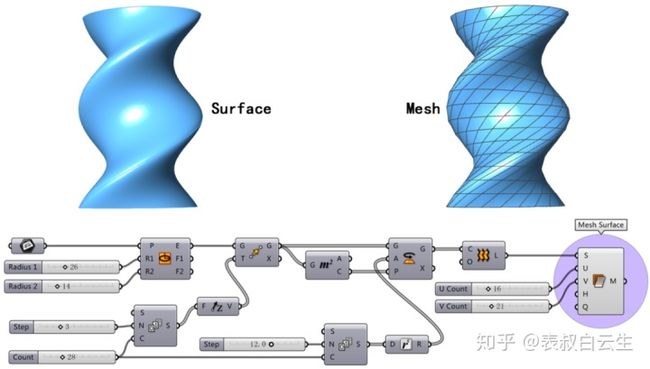
网格同样可以由Nurbs曲面转换得到，通过Mesh Surface运算器可以将曲面转换成四边网格，并可以自定义U向和V向网格的数量。曲面可以通过Mesh Surface运算器转换成网格，并保持原始曲面的UV拓扑结构。

网格同样可以通过Mesh Brep运算器由Brep转换而来，不过由于Brep的UV结构往往比较混乱，生成的网格拓扑关系也比较混乱，难以对其深化处理。通常的做法都是利用UV结构较为规整的单一曲面转换成网格，再对其进行深化处理。

GH中网格框线的开启与关闭可在【Display→ Preview Mesh Edges】进行切换，也可通过快捷键“Ctrl+M”控制网格框线的开启与关闭。

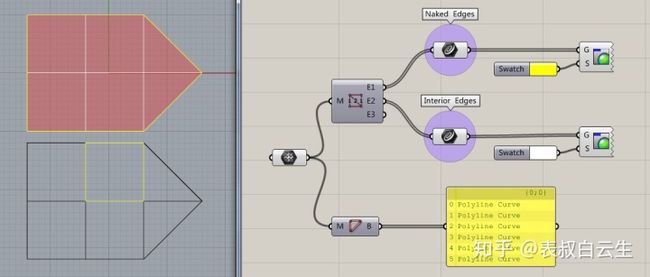
网格边缘分为Naked Edges、Interior Edges、Non-Manifold Edges，用Mesh Edges运算器可将这三类边缘提取出来。其中Naked Edges表示外露边缘线（每个边缘线只属于一个面），Interior Edges表示内部边缘线（两个面共用一个边缘线），Non-Manifold Edges表示非正常边缘线（多于两个面共用一个边缘线）。用Mesh Edges运算器提取出来的边缘线都是断开的Line。

通过Face Boundaries运算器可提取网格每个面的边缘线，其输出的结果是闭合的Polyline Curve,如果将这些Polyline Curve炸开的话，在面与面相交的位置会有重合的边缘线产生。

创建孔洞表皮是GH中比较常见的操作，多数情况下的习惯是用Nurbs来操作的，可是Nurbs所带来的问题就是一旦所开孔洞数量较多的话，整个程序的运行就会变得非常慢。为了提高运算效率，可以通过Mesh的做法来优化整个程序。以下通过一个案例介绍Mesh方法创建孔洞表皮的方法：

（1）为了简化操作可以直接调用曲面，并用Mesh Surface运算器将其转换为网格，U向和V向网格划分的数量可分别设定为32、42。

（2）通过Face Boundaries运算器提取每个网格面的轮廓线，并用Face Normals运算器找到每个网格面的中心点。

（3）由List Length运算器测量网格面的数量，并由Subtraction运算器将总数量减去1。

（4）用Range运算器将0 to 1区间进行等分，等分的段数为网格面的数量减去1。

（5）调入Graph mapper运算器，并将其函数类型改为Sine函数。将等分数值赋予Graph mapper运算器，对其进行函数映射。

（6）由于正弦函数的输出数据区间范围是0 to 1，可通过Bounds、Remap Numbers、Construct Domain三个运算器将函数的输出数据映射到0.2 to 0.8区间范围内。

（7）通过Scale运算器将网格面边缘线依据中心点进行缩放，缩放的比例因子为映射后的数值。

（8）由两个Explode运算器将缩放前后的线框同时炸开，为了保证数据路径一一对应，需要通过右键单击Explode运算器的S输出端，选择Graft将两组数据成树形数据。

（9）通过Flip Curve运算器转换其中一组线的方向，如果不转换方向的话，对应两条线的四个端点的排序就是{0；1；3；2}，这样就需要手工修改Face的顶点排序。

（10）将两组网格面的边缘线继续用Explode运算器炸开，同时右键单击其V输出端，选择Simplify进行路径简化。

（11）用Merge运算器将两组点数据进行合并，那么其输出结果为每个路径下有四个构成网格面的顶点。

（12）最后将点赋予Construct Mesh运算器的V输入端，即可依据顶点的排序创建网格。

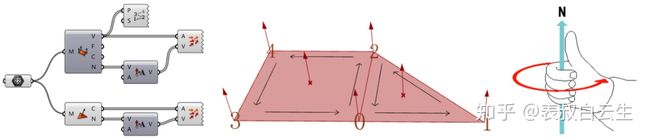
Deconstruct Mesh运算器可以确定网格每个顶点的法线方向，Face Normals运算器可以确定每个网格面中心点的法线方向。网格上点的法线方向遵从右手螺旋定则，两个网格面的顶点排序分别为Q{3,0,2,4}、T{0,1,2}，按照右手螺旋定则，此时网格上点对应的法线方向是向上的。

网格上点的法线应用多伴随形体的变化，以下通过一个案例介绍网格顶点法线方向的应用方法：

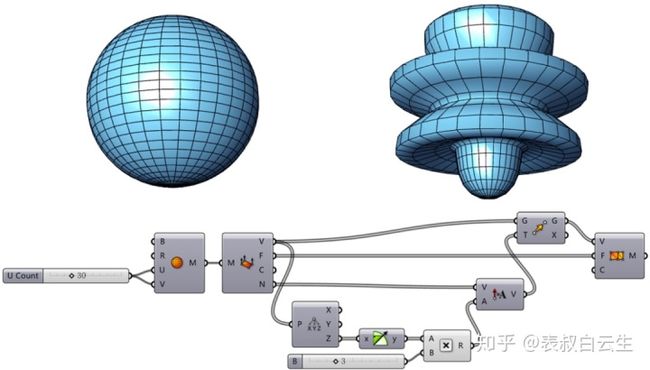
（1）如图所示，用Mesh Sphere运算器创建一个网格球体，其U、V两个方向网格面的数量可同时设定为30。

（2）通过Deconstruct Mesh运算器提取网格面的顶点及其对应的法线方向。

（3）用Deconstruct运算器将网格面的顶点分解为X、Y、Z坐标，并将Z坐标的数值通过Sina运算器进行正弦函数映射。

（4）为了方便后期调整数据，将正弦函数映射后的数值通过Multiplication运算器乘以一个倍增值。将该数值赋予Amplitude运算器的A输入端作为网格顶点法线向量的数值。

（5）将网格顶点通过Move运算器沿着其对应的向量进行移动。

（6）将移动后的顶点由Construct Mesh运算器重新组成网格，其F输入端的网格顶点排序需要与初始网格的顶点排序保持一致。

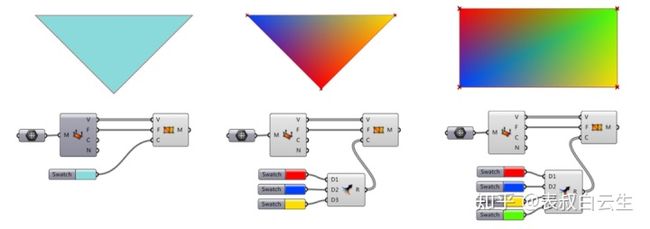
在用Construct Mesh运算器创建网格的时候，可以在其C输入端为网格赋予颜色。如图1-60所示，网格着色的原理就是顶点着色，如果只输入一种颜色，那么网格就会显示该种颜色；如果将顶点指定多种颜色，那么网格将会依据这些顶点颜色生成过渡的渐变色。

网格着色可用来显示分析的结果，以下通过一个案例介绍网格着色的应用方法：

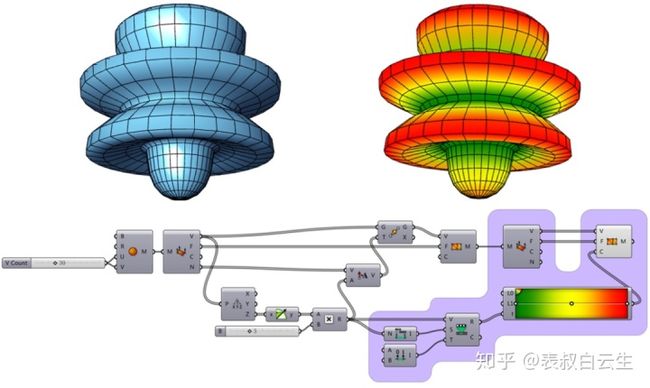
（1）为了简化操作，可以直接调用上一个案例中的网格结果。

（2）为了更直观的显示顶点位移变化的大小，可以通过Gradient Control运算器中的渐变色显示顶点位移的变化趋势。

（3）由于Gradient Control默认的区间范围是0 to 1，可以用数据映射的方法将所有顶点的位移数值映射到0 to 1范围内。

（4）将渐变色赋予Construct Mesh运算器的C输入端，网格的所有顶点将会被赋予相对应的颜色，网格面则会依据四个顶点的颜色生成过渡的渐变色。

公众号 犀牛参数化云平台

犀牛参数化云平台简介：为犀牛和参数化爱好者提供交流的平台，同时也为了推广参数化更多更新的技术应用，欢迎爱好犀牛和GH的朋友一起来交流~