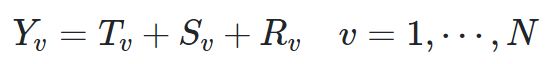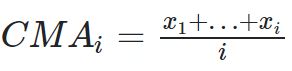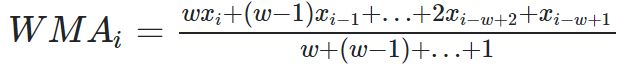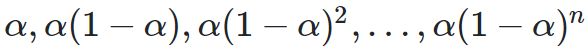时序预测竞赛之异常检测算法综述
本文将介绍在时间序列预测相关问题中常见的异常检测算法,可以很大程度上帮助改善最终预测效果。
异常分类
时间序列的异常检测问题通常表示为相对于某些标准信号或常见信号的离群点。虽然有很多的异常类型,但是我们只关注业务角度中最重要的类型,比如意外的峰值、下降、趋势变化以及等级转换(level shifts)。
常见的异常有如下几种:
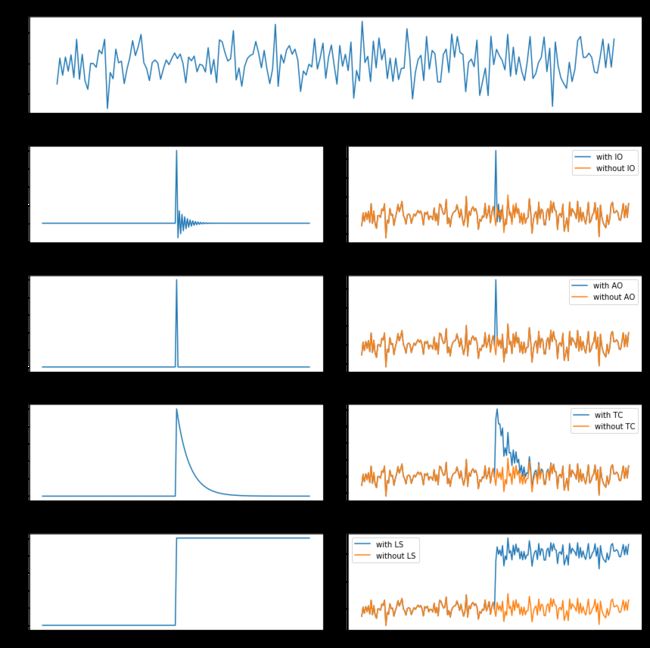
革新性异常:innovational outlier (IO),造成离群点干扰不仅作用于X(T),而且影响T时刻以后序列的所有观察值。
附加性异常:additive outlier (AO),造成这种离群点的干扰,只影响该干扰发生的那一个时刻T上的序列值,而不影响该时刻以后的序列值。
水平移位异常:level shift (LS),造成这种离群点的干扰是在某一时刻T,系统的结构发生了变化,并持续影响T时刻以后的所有行为,在数列上往往表现出T时刻前后的序列均值发生水平位移。
暂时变更异常temporary change (TC):造成这种离群点的干扰是在T时刻干扰发生时具有一定初始效应,以后随时间根据衰减因子的大小呈指数衰减。
上面的解释可能不太容易理解,我们结合图片来看一下:
通常,异常检测算法应该将每个时间点标记为异常/非异常,或者预测某个点的信号,并衡量这个点的真实值与预测值的差值是否足够大,从而将其视为异常。使用后面的方法,你将能够得到一个可视化的置信区间,这有助于理解为什么会出现异常并进行验证。
常见异常检测方法
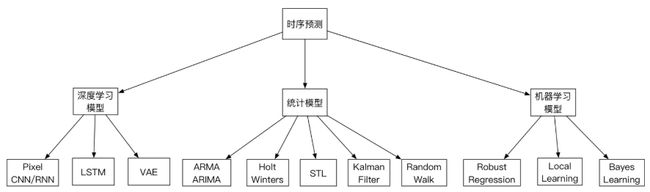
从分类看,当前发展阶段的时序异常检测算法和模型可以分为一下几类:
统计模型:优点是复杂度低,计算速度快,泛化能力强悍。因为没有训练过程,即使没有前期的数据积累,也可以快速的投入生产使用。缺点是准确率一般。但是这个其实是看场景的,并且也有简单的方法来提高业务层面的准确率。这个后面会提到。
机器学习模型:鲁棒性较好,准确率较高。需要训练模型,泛化能力一般。
深度学习模型:普遍需要喂大量的数据,计算复杂度高。整体看,准确性高,尤其是近段时间,强化学习的引入,进一步巩固其准确性方面的领先优势。
3-Sigma
3-Sigma原则又称为拉依达准则,该准则定义如下:假设一组检测数据只含有随机误差,对原始数据进行计算处理得到标准差,然后按一定的概率确定一个区间,认为误差超过这个区间的就属于异常值。
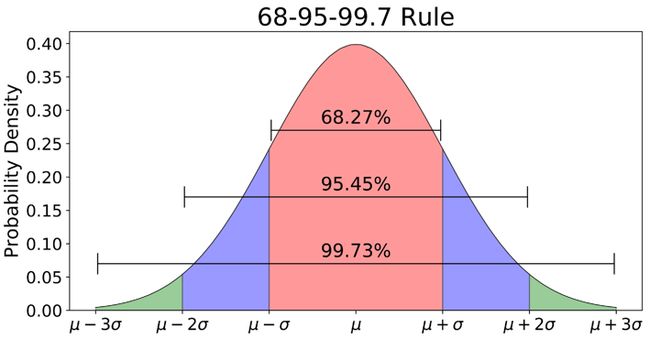
使用3-Sigma的前提是数据服从正态分布,满足这个条件之后,在3-Sigma范围(μ–3σ,μ+3σ)内99.73%的为正常数据,其中σ代表标准差,μ代表均值,x=μ为图形的对称轴。下面是3-Sigma的Python实现:
import numpy as np
def three_sigma(df_col):
'''
df_col:DataFrame数据的某一列
'''
rule = (df_col.mean() - 3 * df_col.std() > df_col) | (df_col.mean() + 3 * df_col.std() < df_col)
index = np.arange(df_col.shape[0])[rule]
out_range = df_col.iloc[index]
return out_range
对于异常值检测出来的结果,有多种处理方式,如果是时间序列中的值,那么我们可以认为这个时刻的操作属于异常的;如果是将异常值检测用于数据预处理阶段,处理方法有以下四种:
删除带有异常值的数据;
将异常值视为缺失值,交给缺失值处理方法来处理;
用平均值进行修正;
当然我们也可以选择不处理。
Grubbs测试
Grubbs’Test为一种假设检验的方法,常被用来检验服从正太分布的单变量数据集(univariate data set)Y 中的单个异常值。若有异常值,则其必为数据集中的最大值或最小值。原假设与备择假设如下:
H0: 数据集中没有异常值
H1: 数据集中有一个异常值
使用Grubbs测试需要总体是正态分布的。算法流程:
样本从小到大排序
求样本的mean和dev
计算min/max与mean的差距,更大的那个为可疑值
求可疑值的z-score (standard score),如果大于Grubbs临界值,那么就是outlier
Grubbs临界值可以查表得到,它由两个值决定:检出水平α(越严格越小),样本数量n,排除outlier,对剩余序列循环做 1-4 步骤。由于这里需要的是异常判定,只需要判断tail_avg是否outlier即可。
from outliers import smirnov_grubbs as grubbs
print(grubbs.test([8, 9, 10, 1, 9], alpha=0.05))
print(grubbs.min_test_outliers([8, 9, 10, 1, 9], alpha=0.05))
print(grubbs.max_test_outliers([8, 9, 10, 1, 9], alpha=0.05))
print(grubbs.max_test_indices([8, 9, 10, 50, 9], alpha=0.05))
S-ESD与S-H-ESD
鉴于时间序列数据具有周期性(seasonal)、趋势性(trend),异常检测时不能作为孤立的样本点处理;故而Twitter的工程师提出了S- ESD (Seasonal ESD)与S-H-ESD (Seasonal Hybrid ESD)算法,将ESD扩展到时间序列数据。
STL分解
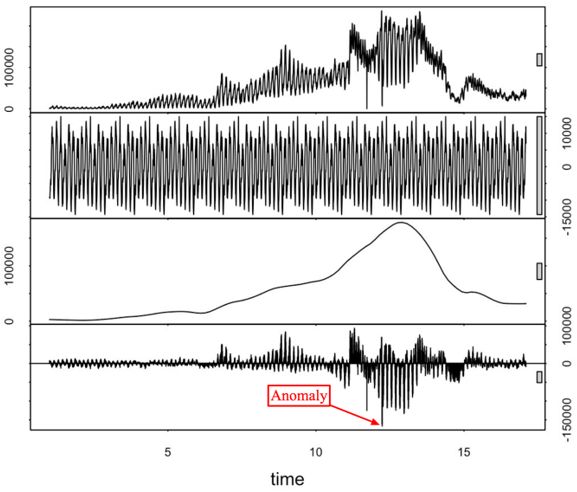
STL (Seasonal-Trend decomposition procedure based on Loess) 为时序分解中一种常见的算法,基于LOESS将某时刻的数据Yv分解为趋势分量(trend component)、季节性分量(seasonal component)和残差(remainder component):
由上到下依次为:原始时间序列和使用 STL 分解得到的季节变化部分、趋势变化部分以及残差部分。
STL分为内循环(inner loop)与外循环(outer loop),其中内循环主要做了趋势拟合与周期分量的计算。假定T(k)v、Sv(k)为内循环中第k-1次pass结束时的趋势分量、周期分量,初始时T(k)v=0;并有以下参数:
n(i)内层循环数
n(o)外层循环数
n(p)为一个周期的样本数
n(s)为Step 2中LOESS平滑参数
n(l)为Step 3中LOESS平滑参数
n(t)为Step 6中LOESS平滑参数
每个周期相同位置的样本点组成一个子序列(subseries),容易知道这样的子序列共有共有n(p)个,我们称其为cycle-subseries。
Python的statsmodels实现了一个简单版的时序分解,通过加权滑动平均提取趋势分量,然后对cycle-subseries每个时间点数据求平均组成周期分量:
使用示例:
import numpy as np
import pandas as pd
from statsmodels.tsa.seasonal import seasonal_decompose
import matplotlib.pyplot as plt
# Generate some data
np.random.seed(0)
n = 1500
dates = np.array('2019-01-01', dtype=np.datetime64) + np.arange(n)
data = 12 * np.sin(2 * np.pi * np.arange(n) / 365) + np.random.normal(12, 2, 1500)
df = pd.DataFrame({'data': data}, index=dates)
# Reproduce the example in OP
seasonal_decompose(df, model='additive', period=1).plot()
plt.show()
S-ESD
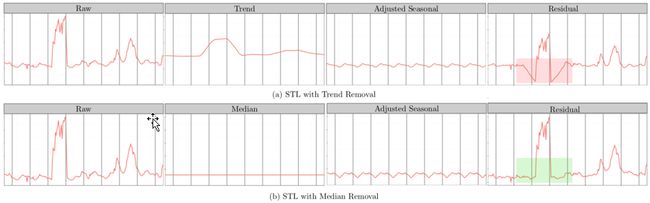
STL将时间序列数据分解为趋势分量、周期分量和余项分量。想当然的解法——将ESD运用于STL分解后的余项分量中,即可得到时间序列上的异常点。但是,我们会发现在余项分量中存在着部分假异常点(spurious anomalies)。如下图所示:
在红色矩形方框中,向下突起点被误报为异常点。为了解决这种假阳性降低准确率的问题,S-ESD算法用中位数(median)替换掉趋势分量;
使用示例:
import numpy as np
import sesd
ts = np.random.random(100)
# Introduce artificial anomalies
ts[14] = 9
ts[83] = 10
outliers_indices = sesd.seasonal_esd(ts, periodicity=20, hybrid=True, max_anomalies=2)
for idx in outliers_indices:
print(f'Anomaly index: {idx}, anomaly value: {ts[idx]}')
移动平均/加权移动平均/指数加权移动平均
移动平均 moving average
给定一个时间序列和窗口长度N,moving average等于当前data point之前N个点(包括当前点)的平均值。不停地移动这个窗口,就得到移动平均曲线。
累加移动平均 cumulative moving average
设{xi:i≥1}是观察到的数据序列。累积移动平均线是所有数据的未加权平均值。如果若干天的值是x1,…,xi,那么:
加权移动平均 weighted moving average
加权移动平均值是先前w个数据的加权平均值
指数加权移动平均 exponential weighted moving average
指数移动与移动平均有些不同:
并没有时间窗口,用的是从时间序列第一个data point到当前data point之间的所有点。
每个data point的权重不同,离当前时间点越近的点的权重越大,历史时间点的权重随着离当前时间点的距离呈指数衰减,从当前data point往前的data point,权重依次为
该算法可以检测一个异常较短时间后发生另外一个异常的情况,异常持续一段时间后可能被判定为正常。
ARIMA 模型
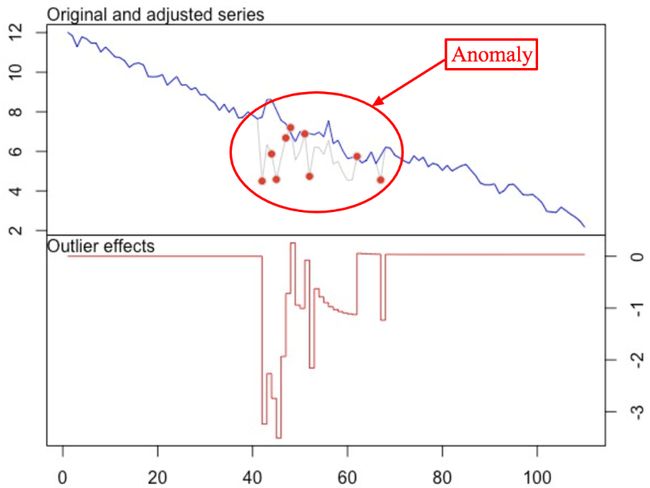
自回归移动平均模型(ARIMA)是一种设计上非常简单的方法,但其效果足够强大,可以预测信号并发现其中的异常。该方法的思路是从过去的几个数据点来生成下一个数据点的预测,在过程中添加一些随机变量(通常是添加白噪声)。以此类推,预测得到的数据点可以用来生成新的预测。很明显:它会使得后续预测信号数据更平滑。使用这种方法最困难的部分是选择差异数量、自回归数量和预测误差系数。另一个障碍是信号经过差分后应该是固定的。也就是说,这意味着信号不应该依赖于时间,这是一个比较显著的限制。
异常检测是利用离群点来建立一个经过调整的信号模型,然后利用t-统计量来检验该模型是否比原模型能更好的拟合数据。
在这种情况下,你可以找到适合信号的 ARIMA 模型,它可以检测出所有类型的异常。
神经网络
与CART方法一样,神经网络有两种应用方式:监督学习和无监督学习。我们处理的数据是时间序列,所以最适合的神经网络类型是 LSTM。如果构建得当,这种循环神经网络将可以建模实现时间序列中最复杂的依赖关系,包括高级的季节性依赖关系。如果存在多个时间序列相互耦合,该方法也非常有用。该领域还在研究中,可以参考这里,构建时序模型需要大量的工作。构建成功完成后,就可能在精确度方面取得优异的成绩。
算法赛交流群已成立
学习数据竞赛,组队参赛,交流分享
如果加入了之前的社群不需要重复添加!