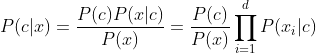机器学习之朴素贝叶斯算法

前言：

        首先应当从概率论说起。接触过概率论的小伙伴一定都知道贝叶斯定理，今天的朴素贝叶斯算法也算贝叶斯定理的一个应用或者说扩展，常应用于文档分类。博主今天将利用朴素贝叶斯算法实现对垃圾邮件的分类。

信息营地：

先验概率：

        之所以叫先验概率，就是在计算目标事件概率之前先知道的某事件概率。先验概率是基于一个已有的样本存在的。这也就是为什么朴素贝叶斯算法可以归入机器学习领域中的原因。计算先验概率的过程可以理解为训练样本的学习过程。

后验概率：

        给定数据样本x时cj成立的概率P(cj  | x )被称为后验概率。个人理解是，在已有数据集的认知下测试样例发生的概率。

贝叶斯定理：

        也就是一个公式 ，来看看怎么推导，之后记住就行了。

 通用公式：

朴素贝叶斯分类器：

        首先需要明确的是，上边公式的分母其实就是P(A)，也就是说在样本确定的情况下，分母的值其实是不会变的。那么的值只受分子的影响。现在我们假设样本之间相互独立，有：

        朴素贝叶斯分类器的训练器的训练过程就是基于训练集D估计类先验概率P(C)，并为每个属性估计条件概率 。

        令表示训练集D中第c类样本组合的集合，则类先验概率：

        对连续属性，可考虑概率密度函数，假定~，其中和分别是第 c类样本在第i个属性上取值的均值和方差，则有：

 拉普拉斯修正：

        若某个属性值在训练集中没有与某个类同时出现过，则训练后的模型会出现 over-fitting 现象。比如“敲声=清脆”测试例，训练集中没有该样例，因此连乘式计算的概率值为0，无论其他属性上明显像好瓜，分类结果都是“好瓜=否”，这显然不合理。

        为了避免其他属性携带的信息，被训练集中未出现的属性值“抹去”，在估计概率值时通常要进行“拉普拉斯修正”：        

        令 N 表示训练集 D 中可能的类别数，表示第i个属性可能的取值数，则贝叶斯公式可修正为：

动手实现：

from array import array
from math import log
def loadDataSet():
    f1 = open("./000/000.txt")
    f0 = open("./delay.txt")
    f0_list = f0.readlines()
    f1_list = f1.readlines()

    postingLost = []
    classVec = []
    # 非垃圾消息
    for line in f0_list:
        line_split = line.split(' ')
        line_split[-1] = line_split[-1][:-1]  # 去除回车
        for i, x in enumerate(line_split):
            low = x.lower()
            line_split[i] = low
        postingLost.append(line_split)
        classVec.append(0)
    # 垃圾消息
    for line in f1_list:
        line_split = line.split(' ')
        line_split[-1] = line_split[-1][:-1]  # 去除回车
        for i, x in enumerate(line_split):
            low = x.lower()  # 开头大写转化为小写
            line_split[i] = low
        postingLost.append(line_split)
        classVec.append(1)

    return postingLost, classVec


def createVocabList(dataset):
    v = set([])
    for doc in dataset:
        v = v | set(doc)  # 用于求两个集合的并集
    return v


def setOfWords2Vec(vocalist, input):
    retv = [0] * len(vocalist)  # 一个其中所含元素都为0的向量
    vocalist = list(vocalist)
    for word in input:
        if word in vocalist:
            retv[vocalist.index(word)] = 1
        else:
            print("词: %s 不在词典集中" % word)
    return retv


# 朴素贝叶斯分类器训练函数
def trainNB0(trainM, trainC):
    numTrain = len(trainM)
    numWords = len(trainM[0])
    pspam = sum(trainC) / float(numTrain)  # 初始化概率
    # 降低乘数为0的影响
    p0num = ones(numWords)
    p1num = ones(numWords)

    p0denom = 2.0
    p1denom = 2.0

    for i in range(numTrain):
        if trainC[i] == 1:
            p1num += trainM[i]
            p1denom += sum(trainM[i])
        else:
            p0num += trainM[i]
            p0denom += sum(trainM[i])
    p1v = log(p1num / p1denom, 10)
    p0v = log(p0num / p0denom, 10)
    return p0v, p1v, pspam


#朴素贝叶斯分类函数
def classifyNB(vec2classify,p0v,p1v,pClass1):
    p1 = sum(vec2classify*p1v)+log(pClass1, 10)
    p0 = sum(vec2classify*p0v)+log(1.0-pClass1, 10)
    if p1>p0:
        return 1
    else:
        return 0


def testingNB():
    listOPosts, listClasses = loadDataSet()
    myVocList = createVocabList(listOPosts)
    trainMat = []
    for postionDoc in listOPosts:
        trainMat.append(setOfWords2Vec(myVocList, postionDoc))
    p0v, p1v, pAb = trainNB0(array(trainMat), array(listClasses))
    testEntry = ['your', 'takeaway', 'delivered', 'designated', \
                 'place.', 'please', 'pick', 'it', 'up', 'as', 'soon', 'possible.', 'rider', 'phone']
    thisDoc = array(setOfWords2Vec(myVocList, testEntry))
    print(testEntry, "测试分类为:", classifyNB(thisDoc, p0v, p1v, pAb))

    testEntry = ['hi,', 'platform', 'presents', 'you', 'with', \
                 'single', 'model', 'lightweight', 'service', 'coupon,', 'valid', 'days,', 'please', 'go', 'to', 'use',
                 'it']
    thisDoc = array(setOfWords2Vec(myVocList, testEntry))
    print(testEntry, "测试分类为:", classifyNB(thisDoc, p0v, p1v, pAb))

testingNB()

结果：

 大致就是这样了。