ML - 线性回归（Linear Regression）

---

线性回归的评估

---

关于线性回归

KNN 主要解决分类问题，线性回归主要解决回归问题。

寻找一条直线，最大程度的“拟合”样本特征和样本输出标记之间的关系。

---

线性回归特点

• 思想简单，实现容易
• 许多强大的非线性模型的基础
• 结果具有很好的可解释性
• 蕴含机器学习中的很多重要思想

---

• 是典型的参数学习；
  对比之下，kNN 是非参数学习
• 只能解决回归问题
  虽然很多分类方法中，线性回归是基础（如 逻辑回归）；
  对比之下，kNN 既可以解决分类 也可以解决回归问题。
• 对数据有假设：线性；
  对比之下，kNN 对数据没有假设。
• 稍微改变线性回归算法，也可以处理非线性问题。

---

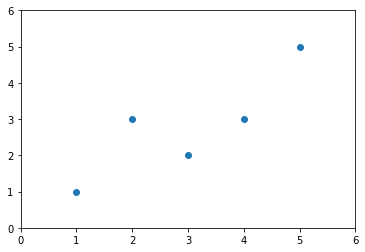
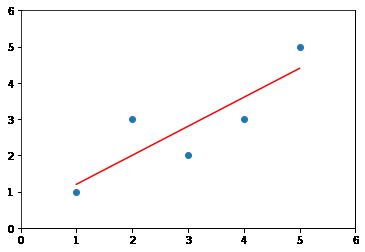
和 kNN 图示的区别


kNN（左图）的 x, y 轴都是样本特征；
线性回归（右图）的 x 轴是特征，y 轴是输出标记 label；

回归问题要预测的是一个具体的数值，这个数值是在连续的空间里的。

---

简单线性回归

样本特征只有一个，称为 简单线性回归。
可以通过简单线性回归，学习到线性回归相应的内容，之后再将它推广到特征有多个的情况（多元线性回归）。

---

算法原理

假没我們找到了最佳批合的直线方程：$ y = ax + b $

则对于毎一个样本点 $x^{(i)}$来说，根据我们的直线方程，预测值为：${\hat{y}}^{(i)}=a{x}^{(i)}+b$。（ $\hat{y}$ 读作 y hat ）

希望这条直线 让 真值$y^{(i)}$ 和 预测值 $\hat{y}^{(i)} $ 差距尽量小。

表达 ${y}^{(i)} $ 和 $ \hat{y}^{(i)}$ 的差距

• ${\hat{y}}^{(i)}-y^{(i)}$ 不合适，因为有可能为负值；
• $|{\hat{y}}^{(i)}-y^{(i)}|$ 不够好，因为绝对值不是处处可导的；绝对值可以后续用来衡量性能。
• $({\hat{y}}^{(i)}-y^{(i)}{)}^2$ 可以，考虑到所有样本，可使用 ${\sum }_{i=1}^m({\hat{y}}^{(i)}-y^{(i)}{)}^2$

所以线性回归计算的目标，是使 ${\sum }_{i=1}^m({\hat{y}}^{(i)}-y^{(i)}{)}^2$ 尽可能小。

将上述式子代入 $ \hat{y}^{(i)} = ax^{(i)} + b$，可转化目标为：
找到 a 和 b，使 ${\sum }_{i=1}^m({\hat{y}}^{(i)}-{ax}^{(i)}-b{)}^2$ 尽可能小。这里 a 和 b 是未知数。

这是一个典型的最小二乘法问题：最小化误差的平方。
通过最小二乘法，可以解出 a 和 b 的表达式：

$$a=\frac{{\sum }_{i=1}^m(x^{(i)}-\overline{x})(y^{(i)}-\overline{y})}{{\sum }_{i=1}^m(x^{(i)}-\overline{x}{)}^2}$$

$b=\overline{y}-a\overline{x}$

$\overline{x}$ 读作 x bar

---

求函数最小值，是一个极值问题，方法为求导；导数为 0 的地方是极值点。

$J(a, b) = \sum^m_{i=1} ( {y}^{(i)} - {ax}^{(i)} - b)^2 $
$ \frac{\alpha J(a,b)}{\alpha b} = 0$
$ \frac{\alpha J(a,b)}{\alpha a} = 0$

---

对b求导比较容易，先计算：

$\frac{\alpha J(a,b)}{\alpha b}={\sum }_{i=1}^{m}2(y^{(i)}-{ax}^{(i)}-b)(-1)=0$

等价于 ${\sum }_{i=1}^m(y^{(i)}-{ax}^{(i)}-b)=0$

${\sum }_{i=1}^m{y}^{(i)}-a{\sum }_{i=1}^m{x}^{(i)}-{\sum }_{i=1}^{m}b)=0$

${\sum }_{i=1}^m{y}^{(i)}-a{\sum }_{i=1}^m{x}^{(i)}-mb=0$

$mb={\sum }_{i=1}^m{y}^{(i)}-a{\sum }_{i=1}^m{x}^{(i)}$

$b=\overline{y}-a\overline{x}$

---

对 a 求导
$\frac{\alpha J(a,b)}{\alpha a}={\sum }_{i=1}^{m}2(y^{(i)}-{ax}^{(i)}-b)(-x^{(i)})=0$

$ \sum_{i=1}^m ({y}^{(i)} - {ax}^{(i)} - b) x^{(i)} = 0$

见上方求出的b 的值带入这个式子，就只剩下 a 这一个未知数
$ \sum_{i=1}^m ( {y}^{(i)} - {ax}^{(i)} - \overline{y} + a\overline{x} ) x^{(i)} = 0$

${\sum }_{i=1}^m(x^{(i)}{y}^{(i)}-a(x^{(i)}{)}^2-x^{(i)}\overline{y}+a\overline{x}{x}^{(i)})$

${\sum }_{i=1}^m(x^{(i)}{y}^{(i)}-x^{(i)}\overline{y}-a(x^{(i)}{)}^2+a\overline{x}{x}^{(i)})$

${\sum }_{i=1}^m(x^{(i)}{y}^{(i)}-x^{(i)}\overline{y})-{\sum }_{i=1}^m(a(x^{(i)}{)}^2-a\overline{x}{x}^{(i)})$

${\sum }_{i=1}^m(x^{(i)}{y}^{(i)}-x^{(i)}\overline{y})-a{\sum }_{i=1}^m((x^{(i)}{)}^2-\overline{x}{x}^{(i)})=0$

求得：
$a=\frac{{\sum }_{i=1}^m(x^{(i)}{y}^{(i)}-x^{(i)}\overline{y})}{{\sum }_{i=1}^m((x^{(i)}{)}^2-\overline{x}{x}^{(i)})}$

---

• $\overline{y}$ 和 $\overline{x}$ 都是常数，可以提取出来;
• ${\sum }_{i=1}^m{x}^{(i)}=m\overline{x}$
• $m \overline{y} = \sum_{i=1}^m y^{(i)} $

${\sum }_{i=1}^m{x}^{(i)}\overline{y}=\overline{y}{\sum }_{i=1}^m{x}^{(i)}=m\overline{y}\cdot \overline{x}$
$=\overline{x}{\sum }_{i=1}^m{y}^{(i)}={\sum }_{i=1}^m\overline{x}{y}^{(i)}={\sum }_{i=1}^m\overline{x}\cdot \overline{y}$

---

以上的推导，可以让 a 的表达式继续变换：

$a=\frac{{\sum }_{i=1}^m(x^{(i)}{y}^{(i)}-x^{(i)}\overline{y})}{{\sum }_{i=1}^m((x^{(i)}{)}^2-\overline{x}{x}^{(i)})}$

$=\frac{{\sum }_{i=1}^m(x^{(i)}{y}^{(i)}-x^{(i)}\overline{y}-\overline{x}{y}^{(i)}+\overline{x}\overline{y})}{{\sum }_{i=1}^m((x^{(i)}{)}^2-\overline{x}{x}^{(i)}-\overline{x}{x}^{(i)}+{\overline{x}}^2)}$

$=\frac{{\sum }_{i=1}^m(x^{(i)}-\overline{x})(y^{(i)}-\overline{y})}{{\sum }_{i=1}^m(x^{(i)}-\overline{x}{)}^2}$

---

如何求解机器学习算法？

找到某一些参数值，使得某一个函数尽可能小，是典型的机器学习的推导思路。换句话说，所谓建模过程，就是找到模型，最大程度的拟合数据。线性回归中，这个模型就是线性方程。

所谓最大的拟合数据，本质是找到一个函数，这个函数称为 损失函数（loss function），度量出模型没有拟合住样本的那一部分（损失的那一部分），希望它尽可能小。

在有的算法中，可能会使用拟合的程度来度量，称这个函数为 效用函数（utility function），希望它尽可能大。

损失函数 和 效用函数 统称为 目标函数；
机器学习通过分析问题，确定问题的损失函数或者效用函数；通过最优化损失函数或者效用函数，获得机器学习的模型。

近乎所有的参数学习算法 都是这样的套路。这个思想的一个学科叫做 最优化原理。

很多问题的本质都是最优化问题，比如 求最短的路径、最小的生成树、总价值最大。

最优化领域有一个分支叫 凸优化。

---

编程实现简单线性回归

import numpy as np
import matplotlib.pyplot as plt
x = np.array([1., 2., 3., 4., 5.])
y = np.array([1., 3., 2., 3., 5.])
plt.scatter(x, y )
plt.axis([0, 6, 0, 6])
# plt.show( )

x_mean = np.mean(x)
y_mean = np.mean(y)
 
num = 0.0
d = 0.0

for x_i, y_i in zip(x, y):
    num += (x_i - x_mean) * (y_i - y_mean)
    d += (x_i - x_mean) ** 2
 
a = num/d
b = y_mean - a * x_mean
a, b
# (0.8, 0.39999999999999947)

 
y_hat = a * x + b
y_hat
# array([1.2, 2. , 2.8, 3.6, 4.4])

# 画图
plt.scatter(x, y)
plt.plot(x, y_hat, color = 'r')
plt.axis([0,6,0,6])

x_predict = 6
y_predict = a * x_predict + b
y_predict
# 5.2

---

向量化运算

使用向量计算可以大幅提高性能。

上述计算的结果可以使用向量表示

$a=\frac{{\sum }_{i=1}^m(x^{(i)}-\overline{x})(y^{(i)}-\overline{y})}{{\sum }_{i=1}^m(x^{(i)}-\overline{x}{)}^2}$

这个表达式 a 的分子分母 同属这个模式：${\sum }_{i=1}^m{w}^{(i)}\cdot v^{(i)}$

对于 $w$ 和 $v$ 两个向量，对应相乘再相加；

$w=(w^{(1)},w^{(1)},...,w^{(m)})$

$v=(v^{(1)},v^{(1)},...,v^{(m)})$

---

封装线性回归类

import numpy as np
  
class SimpleLinearRegression:

    def __init__(self):
        """初始化Simple Linear Regression模型"""
        self.a_ = None
        self.b_ = None

        
    def fit(self, x_train, y_train):
        """根据训练数据集x_train, y_train训练 Simple Linear Regression模型"""
        assert x_train.ndim == 1, "Simple Linear Regressor can only solve single feature training data."
        assert len(x_train) == len(y_train), "the size of x_train must be equal to the size of y_train"

        x_mean = np.mean(x_train)
        y_mean = np.mean(y_train)

        num = 0.0
        d = 0.0

        for x_i, y_i in zip(x, y):
            num += (x_i - x_mean) * (y_i - y_mean)
            d += (x_i - x_mean) ** 2
        
        self.a_ = num/d
        self.b_ = y_mean - self.a_ * x_mean

        return self

     #  向量化运算
    def fit2(self, x_train, y_train):
        """根据训练数据集x_train, y_train训练 Simple Linear Regression模型"""
        assert x_train.ndim == 1, "Simple Linear Regressor can only solve single feature training data."
        assert len(x_train) == len(y_train), "the size of x_train must be equal to the size of y_train"

        x_mean = np.mean(x_train)
        y_mean = np.mean(y_train)

        self.a_ = (x_train - x_mean).dot(y_train - y_mean) / (x_train - x_mean).dot(x_train - x_mean)
        self.b_ = y_mean - self.a_ * x_mean

        return self
    
    def predict(self, x_predict):
        """给定待预测数据集x_predict，返回表示x_predict的结果向量"""
        # x_predict 是一个向量
        assert x_predict.ndim == 1, "Simple Linear Regressor can only solve single feature training data."
        assert self.a_ is not None and self.b_ is not None, "must fit before predict!"

        return np.array([self._predict(x) for x in x_predict])

    
    def _predict(self, x_single):
        """给定单个待预测数据x，返回x的预测结果值"""
        return self.a_ * x_single + self.b_

    
    def score(self, x_test, y_test):
        """根据测试数据集 x_test 和 y_test 确定当前模型的准确度"""

        y_predict = self.predict(x_test)
        return r2_score(y_test, y_predict)

    
    def __repr__(self):
        return "SimpleLinearRegression()"

---

评估方法

理论原理可见：线性回归的评估（MSE、RMSE、MAE、R Square）

import numpy as np
from math import sqrt


def accuracy_score(y_true, y_predict):
    """计算y_true和y_predict之间的准确率"""
    assert len(y_true) == len(y_predict), \
        "the size of y_true must be equal to the size of y_predict"

    return np.sum(y_true == y_predict) / len(y_true)


def mean_squared_error(y_true, y_predict):
    """计算y_true和y_predict之间的MSE"""
    assert len(y_true) == len(y_predict), \
        "the size of y_true must be equal to the size of y_predict"

    return np.sum((y_true - y_predict)**2) / len(y_true)


def root_mean_squared_error(y_true, y_predict):
    """计算y_true和y_predict之间的RMSE"""

    return sqrt(mean_squared_error(y_true, y_predict))


def mean_absolute_error(y_true, y_predict):
    """计算y_true和y_predict之间的RMSE"""
    assert len(y_true) == len(y_predict), \
        "the size of y_true must be equal to the size of y_predict"

    return np.sum(np.absolute(y_true - y_predict)) / len(y_true)


def r2_score(y_true, y_predict):
    """计算y_true和y_predict之间的R Square"""

    return 1 - mean_squared_error(y_true, y_predict)/np.var(y_true)

线性回归是一个典型的参数学习方法

---

使用上方的类

reg1 = SimpleLinearRegression()
reg1.fit(x, y) # SimpleLinearRegression()

      reg1.predict(np.array([x_predict]))

---

向量化运算的性能测试

m = 1000000
big_x = np.random.random(size=m)
big_y = big_x * 2.0 + 3.0 + np.random.normal(size=m)

 %timeit reg1.fit(big_x, big_y)
%timeit reg1.fit2(big_x, big_y)

# 986 µs ± 26.3 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
# 7.56 ms ± 184 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)  

---

sklearn 的线性回归文档：

• linear_model
  https://scikit-learn.org/stable/modules/classes.html#module-sklearn.linear_model

• LinearRegression
  https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html#sklearn.linear_model.LinearRegression

---

多元线性回归

---

线性回归的可解释性

在获取可解释性后，可以有针对性的去采集更多的特征，来更好的描述数据；
所以拿到一组数据，就可以先用线性的方式来看，更快速的分析。

# 对整个数据进行拟合，再进行相应分析

reg = LinearRegression()
reg.fit(X, y)
# LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
 
# 系数
reg.coef_ 
# 结果有正有负，正代表正相关，系数越大代表越相关。
 
'''
    array([-1.06715912e-01,  3.53133180e-02, -4.38830943e-02,  4.52209315e-01,
           -1.23981083e+01,  3.75945346e+00, -2.36790549e-02, -1.21096549e+00,
            2.51301879e-01, -1.37774382e-02, -8.38180086e-01,  7.85316354e-03,
           -3.50107918e-01]) 
'''
 
# 对系数进行排序

np.argsort(reg.coef_)
# array([ 4,  7, 10, 12,  0,  2,  6,  9, 11,  1,  8,  3,  5])
 
boston.feature_names[np.argsort(reg.coef_)]
# array(['NOX', 'DIS', 'PTRATIO', 'LSTAT', 'CRIM', 'INDUS', 'AGE', 'TAX', 'B', 'ZN', 'RAD', 'CHAS', 'RM'], dtype='

 
print(boston.DESCR)
'''
    .. _boston_dataset:
    
    Boston house prices dataset
    ---------------------------
    
    **Data Set Characteristics:**  
    
        :Number of Instances: 506 
    
        :Number of Attributes: 13 numeric/categorical predictive. Median Value (attribute 14) is usually the target.
    
        :Attribute Information (in order):
            - CRIM     per capita crime rate by town
            - ZN       proportion of residential land zoned for lots over 25,000 sq.ft.
            - INDUS    proportion of non-retail business acres per town
            - CHAS     Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
            - NOX      nitric oxides concentration (parts per 10 million)
            - RM       average number of rooms per dwelling
            - AGE      proportion of owner-occupied units built prior to 1940
            - DIS      weighted distances to five Boston employment centres
            - RAD      index of accessibility to radial highways
            - TAX      full-value property-tax rate per $10,000
            - PTRATIO  pupil-teacher ratio by town
            - B        1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
            - LSTAT    % lower status of the population
            - MEDV     Median value of owner-occupied homes in $1000's
    
        :Missing Attribute Values: None
    
        :Creator: Harrison, D. and Rubinfeld, D.L.
    
    This is a copy of UCI ML housing dataset.
    https://archive.ics.uci.edu/ml/machine-learning-databases/housing/


​    
    This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University.
    
    The Boston house-price data of Harrison, D. and Rubinfeld, D.L. 'Hedonic
    prices and the demand for clean air', J. Environ. Economics & Management,
    vol.5, 81-102, 1978.   Used in Belsley, Kuh & Welsch, 'Regression diagnostics
    ...', Wiley, 1980.   N.B. Various transformations are used in the table on
    pages 244-261 of the latter.
    
    The Boston house-price data has been used in many machine learning papers that address regression
    problems.   
         
    .. topic:: References
    
       - Belsley, Kuh & Welsch, 'Regression diagnostics: Identifying Influential Data and Sources of Collinearity', Wiley, 1980. 244-261.
       - Quinlan,R. (1993). Combining Instance-Based and Model-Based Learning. In Proceedings on the Tenth International Conference of Machine Learning, 236-243, University of Massachusetts, Amherst. Morgan Kaufmann.

'''