知识图谱-生物信息学-医学顶刊论文(Briefings in Bioinformatics-2022)：基于异构图GCN和GAT的DTI预测

(2022.4.16)Briefings-DTI-HETA：基于异构图GCN和GAT的DTI预测

目录

• (2022.4.16)Briefings-DTI-HETA：基于异构图GCN和GAT的DTI预测
  • 摘要
  • 1.引言
  • 2.模型方法
    • 2.1 定义
    • 3.1 异构图上的GCN
    • 3.2 图注意机制
    • 3.3 链接预测
  • 4.实验
    • 4.1 案例分析
      论文题目：DTI-HETA: prediction of drug–target interactions based on GCN and GAT on heterogeneous graph
      论文期刊：Briefings in Bioinformatics
      论文地址：https://www.researchgate.net/publication/359770303_DTI-HETA_prediction_of_drug-target_interactions_based_on_GCN_and_GAT_on_heterogeneous_graph?enrichId=rgreq-a5a24fcb10c488ab34ec6a465559eaf7-XXX&enrichSource=Y292ZXJQYWdlOzM1OTc3MDMwMztBUzoxMTQ4OTc1MTU5NzU0NzUzQDE2NTA5NDg0MzMyNTU%3D&el=1_x_2&_esc=publicationCoverPdf

摘要

药物-靶点相互作用(DTI)预测在药物重新定位、药物发现和药物设计中具有重要作用。然而，由于化学和基因组空间大，药物和靶点之间的相互作用复杂，DTI的实验鉴定是昂贵和耗时的。近年来，新兴的图神经网络(GNN)被应用于DTI的预测，因为DTI可以有效地用图表示。然而，其中一些方法仅基于同构图，还有一些方法由两个解耦步骤组成，无法联合训练。为了进一步探索融合异构图信息的基于GNN的DTI预测，本研究将DTI预测视为一个链路预测问题，提出了一种基于注意力机制异构图的端到端模型(DTI-HETA)。该模型首先基于药物-药物、靶标-靶标相似矩阵和DTI矩阵构建异构图；然后，利用GCN得到药物和靶点的嵌入表示。为了突出不同邻域节点在汇聚图卷积信息时对中心节点的贡献，在节点嵌入过程中引入了GAT。然后，利用内积解码器预测DTI。为了评价DTI-HETA的性能，在两个数据集上进行了实验。实验结果表明，该模型优于现有的方法。此外，新DTI的识别表明，DTI-HETA可以作为集成异构图信息预测DTI的强大工具。

1.引言

尽管在药物研究和开发方面取得了许多进展，但传统的药物发现过程仍然是危险、耗时和昂贵的，研究一个新的分子实体大约需要12年、花费18亿美元。目前，加速药物发现过程的关键是确定药物是否能与靶点相互作用。一方面，药物与靶点相互作用的识别有助于有效筛选候选新药。虽然有成千上万的化合物存储在各种数据库中，大多数化合物没有相应的目标信息。随着药物和靶点可用数据的增长，越来越多的学者试图研究识别新的药物-靶点相互作用(DTI)的有效计算方法。传统的计算方法可分为三大类:对接模拟方法、基于配体的方法和文献文本挖掘。近年来，一些研究者开发了一些基于机器学习和深度学习的DTI预测模型，进一步拓展了DTI研究的领域和方向。这种方法不仅考虑了药物之间的相关性，而且考虑了靶点之间的相关性，往往能得到理想的预测结果。新的DTI的发现促进了化合物发展为新的药物。此外，DTI预测可以帮助药物重新定位，确定现有药物的新适应症或靶点，即药物重定位，这是药物发现的另一个关键部分。随着人们对药理学认识的加深，多药的药理学已被广泛接受。药物通常针对多个靶点，而不是单一靶点。此外，同一疾病通常涉及多个靶点。这种多药的药理学特征加速了药物再定位的发展。由于大部分已获批的药物都经过了严格的安全性验证，因此重定位的药物比新药更能快速进入临床阶段，也就可以显著加快药物开发过程。

综上所述，DTI预测对于新药的发现和现有药物的重定位都是至关重要的。同时，DTI预测已成为药物副作用预测、联合用药预测、耐药研究等诸多相关领域的重要前提。

考虑到巨大的化学和基因组空间以及药物和靶点之间复杂的相互作用，通过体内外实验识别DTI仍然是昂贵和耗时的。为了解决这一问题，近年来发展起来的计算预测方法成为不可缺少的技术，并且越来越需要新的方法。计算DTI预测既有利于缩小下游实验室候选药物的候选数量，也有利于加速新药开发。

目前，DTI预测的计算方法主要有三类：基于配体的方法、对接仿真模拟和化学基因组方法。虽然生物学上被广泛接受，但基于配体的方法和对接模拟面临许多限制，比如已知的配体数量不足，蛋白质的三维结构未知等。化学基因组学方法可以进一步分为基于机器学习的方法和基于相似性的方法。在这些化学基因组方法中，基于机器学习和深度学习的模型因其可靠的预测结果而最受关注。在这些方法中，药物和靶点的知识被编码成特征来训练模型。然后利用训练后的模型对新型DTIs进行预测。

这些方法通常同时涉及特征提取和DTI预测，但在模型构建中很少考虑药物-靶标对之间潜在有效的相互作用，不能利用药物-药物和靶标相似关系。此外，这种方法只使用DTI矩阵作为二进制标签矩阵进行训练，而忽略了异构生物数据中包含的信息。

近年来，图神经网络(GNN)的快速发展将深度学习的应用扩展到图领域，相关方法也被应用到药物发现中。基于图的方法大致包括两个步骤：网络构建和DTI预测。这种方法不仅考虑了药物之间的关系，也考虑了靶点之间的关系。然而，现有的方法都是针对同构图设计的。在现实中，药物数据和靶标数据具有多个数据源。通过整合来自异构数据源的各种信息，可以进一步提高DTI预测的准确性。异构网络可以对对象之间的各种相互关系进行编码，近年来受到越来越多的关注。Sun等人使用对称元路径获取异构信息，计算节点之间的相似性。Dong等人通过元路径获取节点序列，使用基于元路径的图嵌入方法在异构图中获取节点嵌入。Fan等人获得了由元路径引导的节点嵌入，并将其用于下游推荐任务。近年来，研究人员尝试使用GNN来分析异构图。Schlichtkrull等在关系建模过程中引入了图卷积神经网络(GCN)来完成节点分类。Wang等在异构图中引入了一种注意力机制。Zhang等人提出了一个可以处理具有不同属性的异构图的模型。Liao等人使用潜在的特征和属性来学习节点嵌入到图中。Yun等提出了图Transformer网络(GTN)来获取异构图中的节点嵌入表示，并将其用于下游任务。

但是，这些方法在数据集成过程中容易造成部分信息的丢失，没有考虑到不同相邻节点在聚合中心节点信息时的贡献，导致预测性能较差。由于从预测任务中分离出特征学习可能不会得到最优解，因此预测模型需要通过端到端的方式进行训练。端到端模型需要大量数据来理解输入和目标之间的复杂关系。同时，训练集正负数据的类不平衡也是对GNN方法预测DTI的挑战。

DTI预测一般包括三个任务:已知药物与靶点的相互作用、已知药物与新靶点的相互作用和新药物与已知靶点的相互作用。我们的研究旨在预测已知药物和靶点之间的相互作用，即确定现有药物的重定位可能性。本研究将DTI预测视为异构图上的链路预测问题，提出了一种新的预测模型DTI-HETA，这是一种基于注意力机制的异构图端到端模型。该模型首先基于给定的药物-药物、靶标-靶标相似矩阵和DTI矩阵构建异构图；然后，利用GCN网络获得药物和靶点的嵌入表示。同时，采用GAT来突出不同邻域节点对聚集图卷积信息的中心节点的贡献。最后，根据药物和靶点的嵌入表示，选择合适的解码器进行预测。

本研究的主要贡献如下:

• 针对异构图设计了一种GCN以充分利用源数据集所携带的信息。
• 采样GAT用于突出相邻节点的贡献。
• 采用端到端方式训练所提出的模型，可以更好地更新模型参数。

本研究使用两个数据集来评估所提出模型的性能，并将其与一些最先进的模型进行比较。实验结果表明，DTI-HETA具有较好的预测性能。此外，本文还对预测最多的DTIs进行了深入的文献调查，发现其中一些预测结果得到了前人研究的支持。综上所述，该模型具有良好的DTI预测能力，为更好地理解药物作用模式和药物再利用提供了一种有前景的方法。

2.模型方法

2.1 定义

本研究将DTI预测视为一个链接预测问题，即通过判断药物节点与目标节点之间是否存在边以及对应的两个实例之间是否存在相互作用来预测。

定义1：设$G=(V,E,\mathbf{A},ϵ)$是个图，其中V是N个节点的集合$\{{\mathbf{v}}_1,{\mathbf{v}}_2,\cdots ,{\mathbf{v}}_n\}$， E为不同节点间的边集合。$\mathbf{A}$和$ϵ$分别表示节点的类型集合和边的类型集合。当$|\mathbf{A}|+|ϵ|>2$时，G是一个异构图。

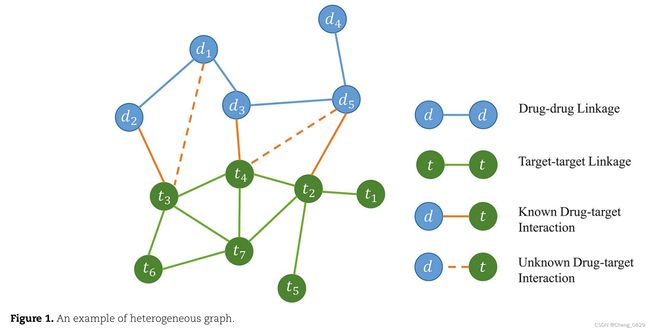
该模型由图构建、图嵌入和链接预测三部分组成。首先，基于输入药物-药物、目标-目标相似矩阵和DTI矩阵构造异构图G；如图1所示，在图G中，$|\mathbf{A}|=2,|ϵ|=3$。通过随机初始化得到节点特征矩阵，利用图嵌入方法获得基于GCN的药物和靶标的嵌入表示。

定义2：异构图中的节点嵌入。给定一个异构图G，节点嵌入的目的是学习一个函数$f$，它将G中的每个节点映射到一个低维空间${\mathbb{R}}^{\mathrm{d}}:f:v\in V\to {\mathbb{R}}^{\mathrm{d}}$，其中$d\ll |V|$。

考虑到相邻节点在聚合过程中对中心节点的贡献不同，本研究引入GAT算法以获得更有意义的节点嵌入。最后，利用内积解码器根据第二步所得到的嵌入表示来预测DTI。该模型采用端到端方式训练，通过梯度下降更新模型中的参数，使损失函数最小。这种端到端训练方法更容易找到针对特定问题的有效模型和嵌入。模型的整个工作流程如图2所示。

3.1 异构图上的GCN

GCN是GNN的一个重要组成部分。与图嵌入中将嵌入表示与下游任务分离相比，GCN先获得节点的低维向量嵌入，然后根据不同的任务，如节点分类、图分类和链接预测，进行端到端训练。

在本研究中，图卷积模块使用图G中的中心节点的相邻节点来定义信息传播框架，这里称为节点的局部计算图。参数和权重在所有局部计算图之间共享，同一局部计算图内应使用相同的信息传播方法。如图2所示，有四种不同的局部计算图：(a)、(b)、©、(d)。(a)中的中心节点为药物d1，其邻近节点均为药物；(b)中的中心节点为药物d3，相邻节点有药物d1、d5和靶标t4两种类型。©和(d)是目标节点位于中心的另外两种情况。将(a)和(b)计算出的同一药物节点的特征相加，得到其嵌入表示。同理，根据©和(d)可得到目标节点的特征表示。节点嵌入计算如下:
$${\mathrm{h}}_{\mathrm{d}}={\mathrm{h}}_{\mathrm{d}}^{(\mathrm{a})}+{\mathrm{h}}_{\mathrm{d}}^{(\mathrm{b})},{\mathrm{h}}_{\mathrm{t}}={\mathrm{h}}_{\mathrm{t}}^{(\mathrm{c})}+{\mathrm{h}}_{\mathrm{t}}^{(\mathrm{d})}\text{\hspace{1em}(1)}$$

其中，${\mathrm{h}}_{\mathrm{d}}$为药物节点d的嵌入表示；${\mathrm{h}}_{\mathrm{d}}^{(\mathrm{a})}$和${\mathrm{h}}_{\mathrm{d}}^{(\mathrm{b})}$分别表示局部计算图(a)和(b)中节点d的隐藏状态；${\mathrm{h}}_{\mathrm{t}}$表示目标节点t的嵌入表示，${\mathrm{h}}_{\mathrm{t}}^{(\mathrm{c})}$和${\mathrm{h}}_{\mathrm{t}}^{(\mathrm{d})}$分别表示节点t在局部计算图©和(d)中的隐藏状态。

在GCN的每一层中，根据原图中边的类型计算4个局部计算图，传播和聚合节点信息。单层图卷积的聚合方法如式(2)所示：
$${\mathrm{h}}_{\mathrm{i}}^{(\mathrm{k}+1)}=\delta \left(\sum _{\tau }\sum _{\mathrm{j}\in {\mathcal{N}}_{\tau }^{\mathrm{i}}}{\mathrm{W}}_{\tau }^{(\mathrm{k})}{\mathrm{h}}_{\mathrm{j}}^{(\mathrm{k})}\right)\text{\hspace{1em}(2)}$$

其中，${\mathrm{h}}_{\mathrm{i}}^{(\mathrm{k})}\in {\mathcal{R}}^{d^{(k)}}$表示GCN第k层节点i的隐藏状态，$d^{(k)}$表示第k层节点嵌入的维度。$\tau$表示异构图G的边的类型，例如药物-药物(dd)，目标-目标(tt)和药物-目标(dt)。$W_{\tau }^{(k)}$是第k层中边类型$\tau$的权值，共享相同边类型的权值。${\mathcal{N}}_{\tau }^i$表示类型$\tau$下节点i的直接邻居集合，包括节点i本身。$\delta$为ReLU激活函数。

**GCN：**聚合第k层邻居信息，得到第k+1层隐藏状态，然后在局部计算图中相加，得到嵌入表示。

3.2 图注意机制

GAT在中心节点信息聚合的过程中为相邻节点分配不同的权重。以节点i和j为例，GAT分别对两个节点进行线性变换，然后使用映射函数${\mathrm{f}}_{\mathrm{a}}$将注意系数${\mathrm{e}}_{\mathrm{i}\mathrm{j}}$分配给图中的节点表示节点j对节点i的影响:
$${\mathrm{e}}_{\mathrm{i}\mathrm{j}}={\mathrm{f}}_{\mathrm{a}}({\mathrm{W}}_{\tau }^{(\mathrm{k})}{\mathrm{h}}_{\mathrm{i}}^{(\mathrm{k})},{\mathrm{W}}_{\tau }^{(\mathrm{k})}{\mathrm{h}}_{\mathrm{j}}^{(\mathrm{k})})\text{\hspace{1em}(3)}$$

在本研究中，${\mathrm{f}}_{\mathrm{a}}$为单层正向传播神经网络，其参数为可学习向量$a_{\tau }^{(k)}$。利用LeakyRelu激活函数对网络进行变换。因此，$e_{ij}$的计算公式如下:
$${\mathrm{e}}_{\mathrm{i}\mathrm{j}}=\sigma ({\mathrm{a}}_{\tau }^{(\mathrm{k})}[{\mathrm{W}}_{\tau }^{(\mathrm{k})}{\mathrm{h}}_{\mathrm{i}}^{(\mathrm{k})}||{\mathrm{W}}_{\tau }^{(\mathrm{k})}{\mathrm{h}}_{\mathrm{j}}^{(\mathrm{k})}])\text{\hspace{1em}(4)}$$

其中||表示拼接算子，$\sigma$表示LeakyRelu函数。

为了比较不同节点间的注意系数，使用softmax函数进行归一化:
$${\alpha }_{\mathrm{i}\mathrm{j}}=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}({\mathrm{e}}_{\mathrm{i}\mathrm{j}})=\frac{\mathrm{e}\mathrm{x}\mathrm{p}({\mathrm{e}}_{\mathrm{i}\mathrm{j}})}{{\sum }_{\mathrm{l}\in {\mathcal{N}}_{\tau }^{\mathrm{i}}}\mathrm{e}\mathrm{x}\mathrm{p}({\mathrm{e}}_{\mathrm{i}\mathrm{l}})}\text{\hspace{1em}(5)}$$

注意力权重的计算过程如图3所示。计算节点i和节点j之间的注意力权重后，可以给中心节点的相邻节点分配不同的权重(注意)。

中心节点i的最终输出嵌入是${\mathcal{N}}_{\tau }^i$中所有节点的加权和。因此，式(2)可改写为：
$${\mathrm{h}}_{\mathrm{i}}^{(\mathrm{k}+1)}=\delta \left(\sum _{\tau }\sum _{\mathrm{j}\in {\mathcal{N}}_{\tau }^{\mathrm{i}}}{\alpha }_{\mathrm{i}\mathrm{j}}{\mathrm{W}}_{\tau }^{(\mathrm{k})}{\mathrm{h}}_{\mathrm{j}}^{(\mathrm{k})}\right)\text{\hspace{1em}(6)}$$

3.3 链接预测

本研究使用内积解码器来预测药物i与靶标j之间的相互作用，并使用下面的交叉熵损失函数来训练模型并更新模型中的参数。
$$\mathrm{L}({\mathrm{d}}_{\mathrm{i}},{\mathrm{t}}_{\mathrm{j}})=-\mathrm{Y}({\mathrm{d}}_{\mathrm{i}},{\mathrm{t}}_{\mathrm{j}})\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{P}({\mathrm{d}}_{\mathrm{i}},{\mathrm{t}}_{\mathrm{j}})-{\mathrm{E}}_{{\mathrm{t}}_{\mathrm{n}}\stackrel{~}{}\mathrm{D}({\mathrm{t}}_{\mathrm{j}})}(1-\mathrm{Y}({\mathrm{d}}_{\mathrm{i}},{\mathrm{t}}_{\mathrm{j}}))\mathrm{l}\mathrm{o}\mathrm{g}(1-\mathrm{P}({\mathrm{d}}_{\mathrm{i}},{\mathrm{t}}_{\mathrm{j}}))\text{\hspace{1em}(7)}$$

$\mathrm{Y}({\mathrm{d}}_{\mathrm{i}},{\mathrm{t}}_{\mathrm{j}})$表示药物节点i与目标节点j之间存在一条边。基于已知的具有相互作用的药物-靶标对$({\mathrm{d}}_{\mathrm{i}},{\mathrm{t}}_{\mathrm{j}})$，可以从所有不与药物$d_i$相互作用的靶标中随机选取一个目标${\mathrm{t}}_{\mathrm{n}}$，形成负样本$({\mathrm{d}}_{\mathrm{i}},{\mathrm{t}}_{\mathrm{n}})$。训练过程中使用的负样本是由负采样方案产生的。最终损失函数定义为:
$$\mathrm{L}=\sum _{({\mathrm{d}}_{\mathrm{i}},{\mathrm{t}}_{\mathrm{n}})\in {ϵ}_{\mathrm{d}\mathrm{t}}}\mathrm{L}({\mathrm{d}}_{\mathrm{i}},{\mathrm{t}}_{\mathrm{n}})\text{\hspace{1em}(8)}$$

其中${ϵ}_{\mathrm{d}\mathrm{t}}$表示G中的药物-靶标集合。

4.实验

4.1 案例分析

接下来，在DTI-HETA预测的前50个新型DTIs中研究几个案例(图13)。

阿匹拉洛定是一种alpha-2型肾上腺素受体，用于治疗眼压升高。DrugBank数据库表明阿匹拉洛定可与肾上腺受体αlpha-2A、αlpha-1A和αlpha-2B相互作用。我们的新预测表明阿匹洛定可以与肾上腺素能受体αlpha-2C相互作用，这也是一种αlpha-2型肾上腺素受体，在中枢神经系统中起着至关重要的作用。先前的一项研究证明阿匹拉洛定可以与ADRA2C直接相互作用，证实了我们的这一新的预测。

达沙替尼是一种酪氨酸激酶抑制剂，用于治疗慢性髓系白血病和急性淋巴细胞白血病。达沙替尼的主要靶点是RhoGEF的BCR激活剂和GTPase-Abl酪氨酸激酶(BCR-ABL)、SRC类、c-KIT、促红细胞生成素肝细胞(EPH)受体A2和血小板衍生生长因子受体β。Erb-b2受体酪氨酸激酶4(ERBB4)是受体酪氨酸激酶EGFR亚类的成员。该基因的突变与多种癌症类型有关，包括黑色素瘤、肺腺癌和成神经管细胞瘤。我们的新预测表明ERBB4可能是达沙替尼的新靶点。这与先前一项研究的结论一致，达沙替尼对ERBB4具有中等亲和力。

伊布鲁替尼是一种抗肿瘤药物，用于治疗套细胞淋巴瘤、慢性淋巴细胞白血病、Waldenström的大球蛋白血症和慢性移植物抗宿主病，是伯顿酪氨酸激酶(BTK)的不可逆强效抑制剂。我们的新预测表明Ibrutinib可以作用于Janus激酶2 (JAK2)，这是一种酪氨酸激酶，在细胞因子和生长因子信号传导中起重要作用。在对伊布鲁替尼的初步表征过程中，发现伊布鲁替尼也能与其他激酶结合。此前的一项研究表明，Ibrutinib通过靶向JAK2增强巨噬细胞介导的抗体依赖性细胞吞噬，而不依赖于btk抑制。

伊布替尼的脱靶效应是有益的，可能为临床应用提供新的适应证。为了进一步验证这种新的交互，进行了计算对接，并利用对接程序AutoDock推断新的预测DTI的可能绑定模式。对接结果表明ibrutinib可以对接JAK2的结构。更具体地说，Ibrutinib通过与残基MLI1202、GLU965和MET964形成氢键与JAK2结合(图14)。

上述案例表明，我们的模型具有良好的DTI预测能力，为理解药物作用模式和药物再利用提供了线索。