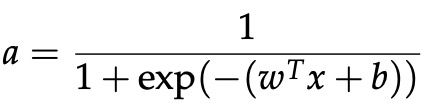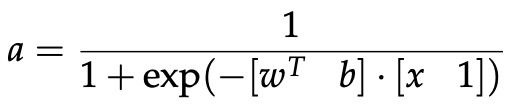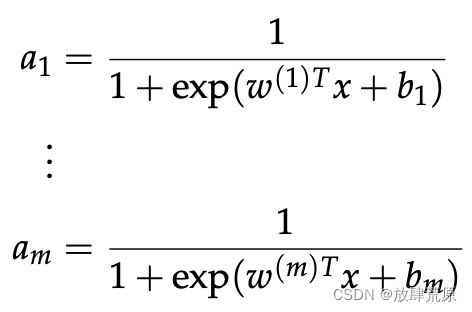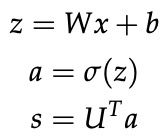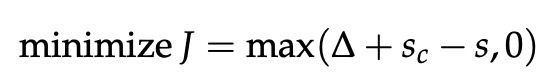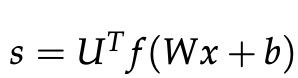CS224n: Natural Language Processing with Deep Learning 笔记、文献及知识点整理（六）神经网络、反向传播（一）

关键词：神经网络 Neural networks、正向计算 Forward computation、反向传播 Backward propagation、神经元 Neuron Units、最大边际损失 Max-margin Loss、梯度检查 Gradient checks、Xavier参数初始化 、学习率 Learning rates、Adagrad。 

本文上一部分请见：CS224n: Natural Language Processing with Deep Learning 笔记、文献及知识点整理（五）词向量（五）_放肆荒原的博客-CSDN博客

讲义：神经网络、反向传播 (Lecture Notes: Neural Networks, Backpropagation)

课程讲师：Christopher Manning、Richard Socher

讲义作者：Rohit Mundra、Amani Peddada、Richard Socher、Qiaojing Yan

这套笔记介绍了单层和多层神经网络，以及它们如何用于分类应用的。 然后讨论如何使用反向传播的分布式梯度下降技术来训练它们。 我们将看到如何使用链式规则来按顺序进行参数更新。 在对神经网络进行严格的数学讨论后，我们还将讨论训练神经网络的一些实用技巧和窍门，包括：神经元单元（非线性）、梯度检查、Xavier 参数初始化、学习率、Adagrad 等。最后，我们将使用循环神经网络作为语言模型来进行进一步学习。

1 神经网络：基础（Neural Networks: Foundations）

在之前的讨论中，我们确定了对非线性分类器的需求，因为大多数数据不是线性可分离的，因此，我们对它们的分类性能是有限的。神经网络是一系列具有非线性决策边界的分类器，如图1所示。现在我们知道了神经网络创建的决策边界，让我们看看它们是如何做到这一点的。

 图 1：我们看到非线性决策边界能够很好地分离数据，这是神经网络的强大之处。

【注：】有趣的事实：
神经网络是受生物学启发的分类器，这就是为什么它们通常被称为“人工神经网络”以将它们与有机分类器区分开来。 然而，在现实中，人类神经网络比人工神经网络更强大、更复杂，通常最好不要在两者之间联想太多。

1.1 一个神经元

神经元：
神经元是神经网络的基本组成部分。 我们将看到，神经元可以是允许非线性在网络中产生的众多功能之一。

神经元是一个通用的计算单元，它接受 n 个输入并产生一个输出。 区分不同神经元输出的是它们的参数（也称为它们的权重）。 最流行的神经元选择之一是“sigmoid”或“二元逻辑回归”单元。 该单元采用 n 维输入向量 x 并产生标量激活（输出）a。 该神经元还与一个 n 维权重向量 w 和一个偏置标量 b 相关联。 这个神经元的输出是：

 我们还可以将上述权重和偏差项组合起来，等价地表示：

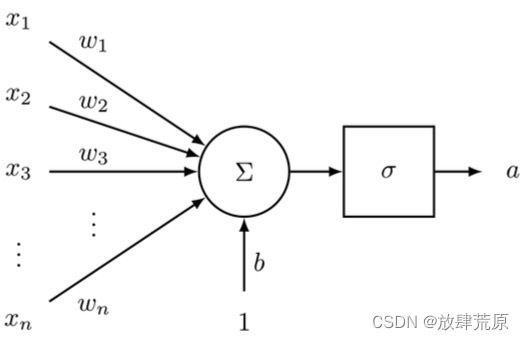
该公式可以以图 2 所示的方式可视化。

 图 2：该图像捕捉了在 sigmoid 神经元中，输入向量 x 如何首先缩放、求和、添加到偏差单元，然后传递给压缩 sigmoid 函数。

1.2 单层神经元

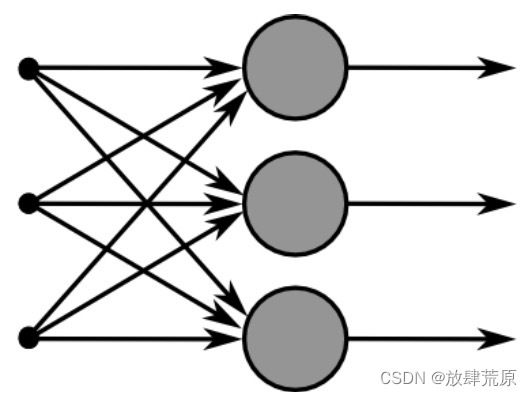
通过考虑输入x作为多个神经元的输入，我们将上述想法扩展到多个神经元，如图3所示。

图 3：此图示意了多个 sigmoid 单元如何堆叠在右侧，所有这些单元都接收相同的输入 x。

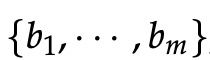如果我们将不同神经元的权重称为并将偏差称为，我们可以说各自的激活是：

我们抽象一下，尽可能简单的定义一些符号，以面对更复杂的网络：

 我们现在可以将缩放和偏差的输出写为：

 sigmoid函数的激活可以写成：

那么这些激活表明了什么呢？我们可以把这些激活看作是某些加权特征组合存在的指标。然后，使用这些激活的组合来执行分类任务。

1.3 前馈计算 Feed-forward Computation

到目前为止，我们已经看到了将输入向量 x ∈ Rn 喂到一层 sigmoid 单元以创建激活 a ∈ Rm。但这背后的直觉是什么呢？我们下面以 NLP 中的命名实体识别 (NER) 问题为例：

"Museums in Paris are amazing"

在这里，我们要对中心词“Paris”是否是一个命名实体进行分类。在这种情况下，我们很可能不仅要捕捉词向量窗口中单词的出现，还要捕捉单词之间的一些其他交互以进行分类。 例如，也许只有当“in”是第二个词时，“Museums”作为第一个词才有意义。这种非线性决策通常无法通过直接喂送到 Softmax 函数的输入来捕获，而是需要对第 1.2 节中讨论的中间层进行评分。 因此，我们可以使用另一个矩阵从激活中生成分类任务的非归一化分数：

 这里f是激活函数。

【注：】单隐层神经网络的维度：如果我们使用 4 维词向量表示每个词，并使用 5 词窗口作为输入，则输入。 如果我们在隐藏层中使用 8 个 sigmoid 单元并从激活中生成 1 个分数输出，则 。然后阶段式前馈计算是 ：

 

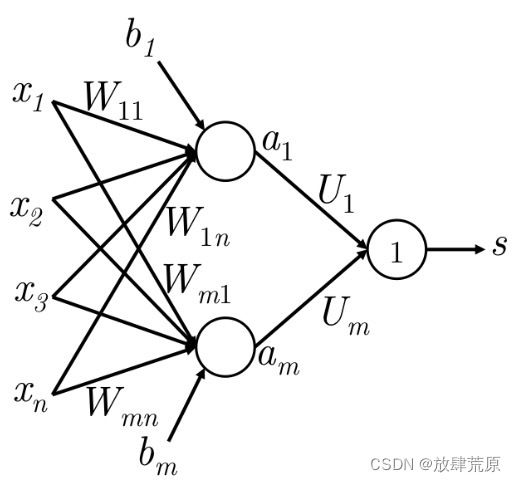
 图4：此图示意了一个简单的前馈网络如何计算其输出

 

1.4 最大边际目标函数

与大多数机器学习模型一样，神经网络也需要一个优化目标，即我们希望分别最小化或最大化的误差或良性度量。 在这里，我们将讨论一种流行的误差指标，称为最大边际目标。 使用此目标背后的想法是确保数据点标记为“真”的计算的分数高于为“假”的分数。

使用上一个例子，如果我们把标签为“真”的窗口“Museums in Paris are amazing”所计算出来的分数称为s，把“假”标签窗口“Not all museums in Paris”计算的分数称为（下标为c表示窗口已“损坏”）。

然后，目标函数最大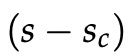化或最小化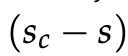。 不过，我们要修改一下目标以确保仅在 时才计算误差。这样做是因为我们只关心“真”数据点比“假”数据点具有更高的分数，其余的无关紧要。 因此，我们希望误差为，这样，我们的优化目标就是：

不过，上述优化目标是有风险的，因为它不能创建安全边际。我们希望标记为“真”的数据点的得分比标记为“假”的数据点的得分高出一些正值∆。换句话说，我们希望在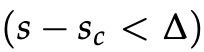时计算误差，而不仅仅只是在 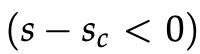时。因此，我们修改了优化目标：

 

我们可以扩大这一边际，使其为 Δ = 1，并让优化问题中的其他参数适应这一点，而不改变性能。 有关这方面的更多信息，请阅读有关函数和几何边距的内容，这是支持向量机研究中经常涉及的主题。最后，我们定义了以下优化目标，我们通过所有训练窗口对其进行了优化：

​​​​​​​​​​​​​​

 在上述公式中，，

【注：】最大边际目标函数常常与支持向量机 (SVM) 相关联 

 

<未完待续......>