目标运动模型建模

目录

1.CV模型

1.1理论介绍

1.2仿真介绍

2.CA模型

2.1理论介绍

2.2仿真介绍

3.CT模型

3.1理论介绍

3.2仿真介绍

4.参考文献

---

1.CV模型

1.1理论介绍

匀速(CV, Constant velocity)模型。

假设目标在二维平面内做匀速直线运动，则离散时间系统下的目标位置与速度的关系可表示为：    

考虑不可能获得目标的精确模型以及许多不可预测的现象，换句话说，也就是目标不可能做绝对匀速运动，其速度必然有一些小的随机波动，即加速度不可能绝对为0，但同时加速度也不会较大，故将这些较小的加速度引起的速度变化看作过程噪声来建模，即为过程噪声。

1.2仿真介绍

仿真条件：

	目标1初始状态	目标2初始状态	过程噪声
二维	(100m,10m,6m/s,5m/s)	(10m,800m,5m/s,-8m/s)	1e-4m/s2
三维	(100m,10m,200m,6m/s,5m/s,-4m/s)	(10m,800m,-100m,5m/s,-8m/s,-2m/s)	1e-4m/s2

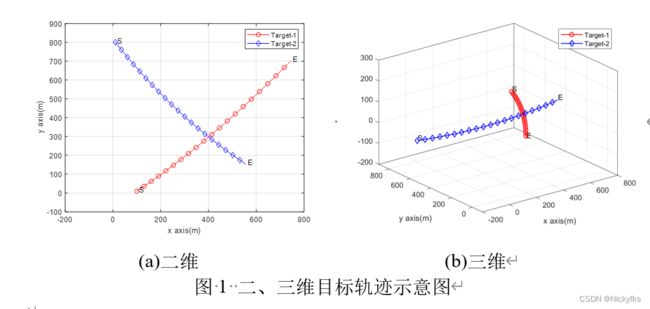
二维CV模型代码

%% 2D-CV Model
clc;clear all;
close all;

%% Initialization
N=100; % Sampling Times
T=1; % Sampling Interval
F=[1 0 T 0;0 1 0 T;0 0 1 0;0 0 0 1]; % State transition matrix
G=[T^2/2 0;0 T^2/2;T 0;0 T]; % Disturbance matrix
w=[1e-4;1e-4]; % System noise matrix
Target_num=2;
X1(:,1)=[100,10,6,5]';
X2(:,1)=[10,800,5,-8]';
Marker={'ro-','bd-'};

%% Target State
for j=1:Target_num
    X=eval(['X' num2str(j) ,';']);
    [X]=Target_State(X,N,F,G,w);
    eval(['X' num2str(j) '=' 'X' , ';']);
    clear X;
end

%% Figure
% Track
figure;
hold on
for j=1:Target_num
    X=eval(['X' num2str(j) ,';']);
    plot(X(1,:),X(2,:),Marker{j},'Markerindices',1:5:N,'linewidth',1)
    text(X(1,1)+10,X(2,1)+10,'S')
    text(X(1,N)+10,X(2,N)+10,'E')
    clear X;
end
hold off
legend('Target-1','Target-2','Location','Northeast')
xlabel('x axis(m)')
ylabel('y axis(m)')
grid on
box on
xlim([-200,800])
ylim([-100,900])

%% Target State
function [X]=Target_State(X,N,F,G,w)
for k=1:N-1
    X(:,k+1)=F*X(:,k)+G*[normrnd(0,w(1),1,1);normrnd(0,w(2),1,1)]; % Target State Equation
end
end

2.CA模型

2.1理论介绍

匀加速(CA, Constant acceleration)模型。

假设目标在二维平面内做匀加速直线运动，则离散时间系统下的目标位置与速度的关系可表示为：

 可以看出相较于CV模型，CA模型除了加速度外，还有一定的随机扰动对速度有着影响。

2.2仿真介绍

仿真条件：

	目标1初始状态	目标2初始状态	过程噪声
二维	(100m,10m,6m/s,5m/s,0.01 m/s2,0.04m/s2)	(10m,800m,5m/s,-8m/s,0.01 m/s2,0.03 m/s2)	1e-4m/s2
三维	(100m,10m,300m,6m/s,5m/s,-4m/s ,0.01m/s2,0.04m/s2,-0.02m/s2)	(10m,800m,-100m,5m/s ,-8m/s,-2m/s,0.01m/s2,0.03m/s2,0.01m/s2)	1e-4m/s2

 二维CA模型代码

%% 2D-CA Model
clc;clear all;
close all;

%% Initialization
N=100; % Sampling Times
T=1; % Sampling Interval
F=[1 0 T 0 T^2/2 0;0 1 0 T 0 T^2/2;0 0 1 0 T 0;0 0 0 1 0 T;0 0 0 0 1 0;0 0 0 0 0 1]; % State transition matrix
G=[T^2/2 0;0 T^2/2;T 0;0 T;1 0;0 1]; % Disturbance matrix
w=[1e-4;1e-4]; % System noise matrix
Target_num=2;
X1(:,1)=[100,10,6,5,0.01,0.04]';
X2(:,1)=[10,800,5,-8,0.01,0.03]';
Marker={'ro-','bd-'};

%% Target State
for j=1:Target_num
    X=eval(['X' num2str(j) ,';']);
    [X]=Target_State(X,N,F,G,w);
    eval(['X' num2str(j) '=' 'X' , ';']);
    clear X;
end

%% Figure
% Track
figure;
hold on
for j=1:Target_num
    X=eval(['X' num2str(j) ,';']);
    plot(X(1,:),X(2,:),Marker{j},'Markerindices',1:5:N,'linewidth',1)
    text(X(1,1)+10,X(2,1)+10,'S')
    text(X(1,N)+10,X(2,N)+10,'E')
    clear X;
end
hold off
legend('Target-1','Target-2','Location','Northeast')
xlabel('x axis(m)')
ylabel('y axis(m)')
grid on
box on
xlim([-200,800])
ylim([-100,900])

%% Target State
function [X]=Target_State(X,N,F,G,w)
for k=1:N-1
    X(:,k+1)=F*X(:,k)+G*[normrnd(0,w(1),1,1);normrnd(0,w(2),1,1)]; % Target State Equation
end
end

3.CT模型

3.1理论介绍

匀速转弯运动(CT, Coordinate turn)模型，也叫做协同转弯或坐标转弯模型。具体推导过程不在此处给出，直接给出目标状态方程。

3.2仿真介绍

仿真条件：

	目标1初始状态	目标2初始状态	过程噪声
二维	(100m,10m,6m/s,5m/s) 0.8*pi/180	(10m,800m,5m/s,-8m/s) -0.5*pi/180	1e-4m/s2

 二维CT模型代码

%% 2D-CT Model
clc;clear all;
close all;

%% Initialization
N=100; % Sampling Times
T=1; % Sampling Interval
G=[T^2/2 0;0 T^2/2;T 0;0 T]; % Disturbance matrix
w=[1e-4;1e-4]; % System noise matrix
Target_num=2;
omega1=0.8*pi/180;
omega2=-0.5*pi/180;
F1=[1 0 sin(omega1*T)/omega1 (cos(omega1*T)-1)/omega1;0 1 (1-cos(omega1*T))/omega1 sin(omega1*T)/omega1;0 0 cos(omega1*T) -sin(omega1*T);0 0 sin(omega1*T) cos(omega1*T)]; % State transition matrix
F2=[1 0 sin(omega2*T)/omega2 (cos(omega2*T)-1)/omega2;0 1 (1-cos(omega2*T))/omega2 sin(omega2*T)/omega2;0 0 cos(omega2*T) -sin(omega2*T);0 0 sin(omega2*T) cos(omega2*T)]; % State transition matrix
X1(:,1)=[100,10,6,5]';
X2(:,1)=[10,800,5,-8]';
Marker={'ro-','bd-'};

%% Target State
for j=1:Target_num
    X=eval(['X' num2str(j) ,';']);
    F=eval(['F' num2str(j) ,';']);
    [X]=Target_State(X,N,F,G,w);
    eval(['X' num2str(j) '=' 'X' , ';']);
    clear X;
end

%% Figure
% Track
figure;
hold on
for j=1:Target_num
    X=eval(['X' num2str(j) ,';']);
    plot(X(1,:),X(2,:),Marker{j},'Markerindices',1:5:N,'linewidth',1)
    text(X(1,1)+10,X(2,1)+10,'S')
    text(X(1,N)+10,X(2,N)+10,'E')
    clear X;
end
hold off
legend('Target-1','Target-2','Location','Northeast')
xlabel('x axis(m)')
ylabel('y axis(m)')
grid on
box on
xlim([-100,400])
ylim([-200,900])

%% Target State
function [X]=Target_State(X,N,F,G,w)
for k=1:N-1
    X(:,k+1)=F*X(:,k)+G*[normrnd(0,w(1),1,1);normrnd(0,w(2),1,1)]; % Target State Equation
end
end

4.参考文献

何友、修建娟、关欣. 雷达数据处理及应用 [M]. 电子工业出版社, 2013.