机器学习之高斯混合模型(GMM)及python实现

高斯混合模型

高斯混合模型简介:
高斯混合模型是一种无监督聚类算法，一般使用EM算法进行求解。
Kmeans VS GMM：Kmeans算法本质上用的也是EM算法求解的。

本章节内容参考了李航博士的《统计学习方法》
本节不同之处在于分析讨论了多维度空间的高斯混合模型

1 高斯混合模型推导

1.1 高斯混合模型

定义：高斯混合模型是指具有如下形式的概率分布模型：

$$p(y|\theta )=\sum _{k=1}^K{\alpha }_k\varphi (y|{\theta }_k)\text{\hspace{1em}(1)}$$

其中，${\varphi }_k$是系数，${\varphi }_k\ge 0$, ${\sum }_{k=1}^K{\alpha }_k=1$; $\varphi (y|{\theta }_k)$是高斯分布密度函数，${\theta }_k=({\mu }_k,\Sigma )$,

$$\varphi (y|{\theta }_k)=\frac{1}{(2\pi {)}^{\frac{D}{2}}||\Sigma |{|}^{\frac{1}{2}}}exp[-\frac{1}{2}(y-\mu {)}^T{\Sigma }^{-1}(y-\mu )]\text{\hspace{1em}(2)}$$

称为第$k$个分模型，其中$D$是当个特征的特征维度。

$\Sigma$的解释：
$\Sigma$是对称矩阵，${\Sigma }^T=\Sigma$

1.2 高斯混合模型参数估计的EM算法

假设观测数据$y_1,y_2,...,y_N$（每个样本维度是$D$）由高斯混合模型生成,
$$p(y|\theta )=\sum _{k=1}^K{\alpha }_k\varphi (y|{\theta }_k)\text{\hspace{1em}(3)}$$

其中，$\theta =({\alpha }_1,{\alpha }_2,...,{\alpha }_K;{\theta }_1,{\theta }_2,...,{\theta }_K)$.

设想样本是这样产生的：
1.依据概率${\alpha }_k$, 选择对应的高斯分布模型；
2.依据高斯分布模型生成观测数据。

对于已知的观测数据，反映某个观测数据$y_j$来自哪一个分模型是未知的，这也就是这个模型中的隐变量，以${\gamma }_{jk}$表示。

加入隐变量可以得到全变量的似然函数：

$$p(y,\gamma |\theta )=\prod _{j=1}^N\prod _{k=1}^K[{\alpha }_k\varphi (y|{\theta }_k){]}^{{\gamma }_{jk}}\text{\hspace{1em}(4)}$$

这个有一个点需要说明一下：
就是(3)式和(4)的表达式是有区别的。通俗的说(3)式是求和形式，而(4)式是求积的形式。
这是因为(3)式是对模型的表示，即表示模型的构成；而(4)式是所有变量对于单个变量的似然函数表示。

对应的对数似然函数：

$$\begin{array}{rl}\log p(y,\gamma |\theta )& =\log \prod _{j=1}^N\prod _{k=1}^K[{\alpha }_k\varphi (y_j|{\theta }_k){]}^{{\gamma }_{jk}}\\ & =\sum _{j=1}^N\sum _{k=1}^K{\gamma }_{jk}\log [{\alpha }_k\varphi (y_j|{\theta }_k)]\\ & =\sum _{j=1}^N\sum _{k=1}^K{\gamma }_{jk}[\log {\alpha }_k+\log \varphi (y_j|{\theta }_k)]\\ & =\sum _{k=1}^K[\sum _{j=1}^N{\gamma }_{jk}\log {\alpha }_k+\sum _{j=1}^N{\gamma }_{jk}\log \varphi (y_j|{\theta }_k)]\end{array}$$

E 步：

隐变量${\gamma }_{jk}$表示观测数据$y_j$来自哪一个分模型，所以：

$${\hat{\gamma }}_{jk}=\frac{{\alpha }_k\varphi (y_i|{\theta }_k)}{{\sum }_{k=1}^K{\alpha }_k\varphi (y_i|{\theta }_k)}$$

又有：

$$Q(\theta ,{\theta }^{(i)})=\sum _{k=1}^K[\sum _{j=1}^N{\hat{\gamma }}_{jk}\log {\alpha }_k+\sum _{j=1}^N{\hat{\gamma }}_{jk}\log \varphi (y_j|{\theta }_k)]$$

将（2）式带入得：

$$Q(\theta ,{\theta }^{(i)})=\sum _{k=1}^K\{\sum _{j=1}^N{\hat{\gamma }}_{jk}\log {\alpha }_k+\sum _{j=1}^N{\hat{\gamma }}_{jk}\log \frac{1}{(2\pi {)}^{\frac{D}{2}}||{\Sigma }_k|{|}^{\frac{1}{2}}}exp[-\frac{1}{2}(y_j-{\mu }_k{)}^T{\Sigma }_k^{-1}(y_j-{\mu }_k)]\}$$

上式展开得：

$$Q(\theta ,{\theta }^{(i)})=\sum _{k=1}^K\{\sum _{j=1}^N{\hat{\gamma }}_{jk}\log {\alpha }_k-\sum _{j=1}^N{\hat{\gamma }}_{jk}\log (2\pi {)}^{\frac{D}{2}}-\sum _{j=1}^N\frac{{\hat{\gamma }}_{jk}}{2}\log ||{\Sigma }_k||-\sum _{j=1}^N{\hat{\gamma }}_{jk}[\frac{1}{2}(y_j-{\mu }_k{)}^T{\Sigma }_k^{-1}(y_j-{\mu }_k)]\}$$

可以从matrix cookbook 找到矩阵偏导

1.求$\mu$
先整理出来含有$\mu$的项：

$$L({\mu }_k)=-\sum _{j=1}^N{\hat{\gamma }}_{jk}[\frac{1}{2}(y_j-{\mu }_k{)}^T{\Sigma }_k^{-1}(y_j-{\mu }_k)]$$

$$\frac{\partial L({\mu }_k)}{\partial {\mu }_k}=\sum _{j=1}^N{\hat{\gamma }}_{jk}{\Sigma }_k^{-1}(y_j-{\mu }_k))$$

令$\frac{\partial L({\mu }_k)}{\partial {\mu }_k}=0$ 得：

$${\hat{\mu }}_k=\frac{{\sum }_{j=1}^N{\hat{\gamma }}_{jk}{y}_j}{{\sum }_{j=1}^N{\hat{\gamma }}_{jk}}$$

2.求${\Sigma }_k$：
同样的先整理出来含有$\Sigma$的项：

$$L({\Sigma }_k)=-\sum _{j=1}^N\frac{{\hat{\gamma }}_{jk}}{2}\log ||{\Sigma }_k||-\sum _{j=1}^N{\hat{\gamma }}_{jk}[\frac{1}{2}(y_j-{\mu }_k{)}^T{\Sigma }_k^{-1}(y_j-{\mu }_k)]$$

求导取零可以得到：

$${\hat{\Sigma }}_k=\frac{{\sum }_{j=1}^N{\hat{\gamma }}_{jk}(y_j-{\mu }_k)(y_j-{\mu }_k{)}^T}{{\sum }_{j=1}^N{\hat{\gamma }}_{jk}}$$

3.最后求${\alpha }_k$：

$$L({\alpha }_k)=\sum _{j=1}^N{\hat{\gamma }}_{jk}\log {\alpha }_k$$

加上限制条件：

$$\sum _{k=1}^K{\alpha }_k=1\text{\hspace{1em}(5)}$$

用朗格朗日函数：

$$L({\alpha }_k,\lambda )=\sum _{j=1}^N{\hat{\gamma }}_{jk}\log {\alpha }_k+\lambda (\sum _{k=1}^K{\alpha }_k-1)$$

得到：

$$\frac{\partial L({\alpha }_k)}{\partial {\alpha }_k}=\sum _{j=1}^N{\hat{\gamma }}_{jk}\frac{1}{{\alpha }_k}+\lambda =0$$

则：

$${\alpha }_k=\frac{{\sum }_{j=1}^N{\hat{\gamma }}_{jk}}{-\lambda }\text{\hspace{1em}(6)}$$

将(5)式带入(6)式得：

$$\sum _{k=1}^K\sum _{j=1}^N{\hat{\gamma }}_{jk}=-\lambda$$

因为：

$$\sum _{k=1}^K{\hat{\gamma }}_{jk}=1$$

所以：

$$-\lambda =N$$

故：

$${\alpha }_k=\frac{{\sum }_{j=1}^N{\hat{\gamma }}_{jk}}{N}$$

2 高斯混合模型python实现

2.1 模型实现

import numpy as np
np.random.seed(None)


class MyGMM(object):
    def __init__(self, K=3):
        """
        高斯混合模型，用EM算法进行求解
        :param K: 超参数，分类类别

        涉及到的其它参数：
        :param N: 样本量
        :param D: 单个样本的维度
        :param alpha: 模型参数，高斯函数的系数，决定高斯函数的高度，维度（K）
        :param mu: 模型参数，高斯函数的均值，决定高斯函数的中型位置，维度（K,D）
        :param Sigma: 模型参数，高斯函数的方差矩阵，决定高斯函数的形状，维度（K,D,D）
        :param gamma: 模型隐变量，决定单个样本具体属于哪一个高斯分布，维度(N,K)
        """
        self.K = K
        self.params = {
            'alpha': None,
            'mu': None,
            'Sigma': None,
            'gamma': None
        }

        self.N = None
        self.D = None

    def __init_params(self):
        # alpha 需要满足和为1的约束条件
        alpha = np.random.rand(self.K)
        alpha = alpha / np.sum(alpha)
        mu = np.random.rand(self.K, self.D)
        Sigma = np.array([np.identity(self.D) for _ in range(self.K)])
        # 虽然gamma有约束条件，但是第一步E步时会对此重新赋值，所以可以随意初始化
        gamma = np.random.rand(self.N, self.K)

        self.params = {
            'alpha': alpha,
            'mu': mu,
            'Sigma': Sigma,
            'gamma': gamma
        }

    def _gaussian_function(self, y_j, mu_k, Sigma_k):
        '''
        计算高纬度高斯函数
        :param y_j: 第j个观测值
        :param mu_k: 第k个mu值
        :param Sigma_k: 第k个Sigma值
        :return:
        '''
        # 先取对数
        n_1 = self.D * np.log(2 * np.pi)
        # 计算数组行列式的符号和（自然）对数。
        _, n_2 = np.linalg.slogdet(Sigma_k)

        # 计算矩阵的（乘法）逆矩阵。
        n_3 = np.dot(np.dot((y_j - mu_k).T, np.linalg.inv(Sigma_k)), y_j - mu_k)
        
        # 返回是重新取指数抵消前面的取对数操作
        return np.exp(-0.5 * (n_1 + n_2 + n_3))

    def _E_step(self, y):
        alpha = self.params['alpha']
        mu = self.params['mu']
        Sigma = self.params['Sigma']

        for j in range(self.N):
            y_j = y[j]
            gamma_list = []
            for k in range(self.K):
                alpha_k = alpha[k]
                mu_k = mu[k]
                Sigma_k = Sigma[k]
                gamma_list.append(alpha_k * self._gaussian_function(y_j, mu_k, Sigma_k))

            # 对隐变量进行迭代跟新
            self.params['gamma'][j, :] = np.array([v / np.sum(gamma_list) for v in gamma_list])

    def _M_step(self, y):
        mu = self.params['mu']
        gamma = self.params['gamma']
        for k in range(self.K):
            mu_k = mu[k]
            gamma_k = gamma[:, k]
            gamma_k_j_list = []
            mu_k_part_list = []
            Sigma_k_part_list = []
            for j in range(self.N):
                y_j = y[j]
                gamma_k_j = gamma_k[j]
                gamma_k_j_list.append(gamma_k_j)

                # mu_k的分母的分母列表
                mu_k_part_list.append(gamma_k_j * y_j)

                # Sigma_k的分母列表
                Sigma_k_part_list.append(gamma_k_j * np.outer(y_j - mu_k, (y_j - mu_k).T))

            # 对模型参数进行迭代更新
            self.params['mu'][k] = np.sum(mu_k_part_list, axis=0) / np.sum(gamma_k_j_list)
            self.params['Sigma'][k] = np.sum(Sigma_k_part_list, axis=0) / np.sum(gamma_k_j_list)
            self.params['alpha'][k] = np.sum(gamma_k_j_list) / self.N

    def fit(self, y, max_iter=100):
        y = np.array(y)
        self.N, self.D = y.shape
        self.__init_params()

        for _ in range(max_iter):
            self._E_step(y)
            self._M_step(y)

2.1 模型检测

def get_samples(n_ex=1000, n_classes=3, n_in=2, seed=None):
    # 生成100个样本，为了能够在二维平面上画出图线表示出来，每个样本的特征维度设置为2
    from sklearn.datasets.samples_generator import make_blobs
    from sklearn.model_selection import train_test_split
    y, _ = make_blobs(
        n_samples=n_ex, centers=n_classes, n_features=n_in, random_state=seed)
    return y


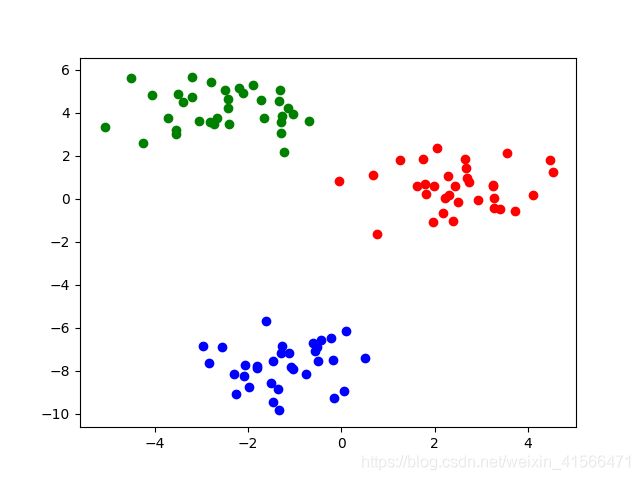
def run_my_model():
    from matplotlib import pyplot as plt
    my = MyGMM()
    y = get_samples()
    my.fit(y)

    max_index = np.argmax(my.params['gamma'], axis=1)
    print(max_index)

    k1_list = []
    k2_list = []
    k3_list = []

    for y_i, index in zip(y, max_index):
        if index == 0:
            k1_list.append(y_i)
        elif index == 1:
            k2_list.append(y_i)
        else:
            k3_list.append(y_i)
    k1_list = np.array(k1_list)
    k2_list = np.array(k2_list)
    k3_list = np.array(k3_list)

    plt.scatter(k1_list[:, 0], k1_list[:, 1], c='red')
    plt.scatter(k2_list[:, 0], k2_list[:, 1], c='blue')
    plt.scatter(k3_list[:, 0], k3_list[:, 1], c='green')
    plt.show()

留问题：模型里面没有终止条件，该如何办？

参考资料：
《统计学习方法》 李航著