pca降维
两个矩阵相乘的意义是将右边矩阵中的每一列向量 ai 变换到左边矩阵中以每一行行向量为基所表示的空间中去
选择不同的基可以对同样一组数据给出不同的表示,如果基的数量少于向量本身的维数,则可以达到降维的效果。
将一组 N 维向量降为 K 维,其目标是选择 K 个单位正交基,使得原始数据变换到这组基上后,各变量两两间协方差为 0(保证两个变量是不相关的),而变量方差则尽可能大(在正交的约束下,取最大的 K 个方差)。
具体原理:【机器学习】降维——PCA(非常详细) - 知乎 (zhihu.com)
import matplotlib.pyplot as plt
#导入鸢尾花数据集
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
import numpy as np
#2.提取数据集
iris = load_iris()
y = iris.target
X = iris.data
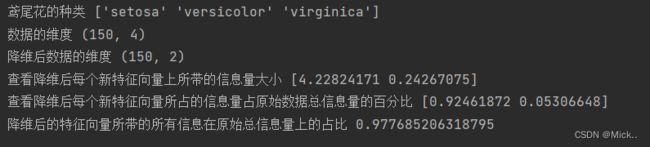
print('鸢尾花的种类',iris.target_names)
print('数据的维度',X.shape)
pca = PCA(n_components=2) #实例化
pca = pca.fit(X) #拟合模型
X_dr = pca.transform(X) #获取新矩阵
print('降维后数据的维度',X_dr.shape)
#属性explained_variance_,查看降维后每个新特征向量上所带的信息量大小(可解释性方差的大小)
print('查看降维后每个新特征向量上所带的信息量大小',pca.explained_variance_)
# 属性explained_variance_ratio_,查看降维后每个新特征向量所占的信息量占原始数据总信息量的百分比 .又叫做可解释方差贡献率
print('查看降维后每个新特征向量所占的信息量占原始数据总信息量的百分比',pca.explained_variance_ratio_)
#整个降维后的特征向量所带的所有信息在原始总信息量上的占比。
print('降维后的特征向量所带的所有信息在原始总信息量上的占比',pca.explained_variance_ratio_.sum())
import matplotlib.pyplot as plt
#导入鸢尾花数据集
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
import numpy as np
#2.提取数据集
iris = load_iris()
y = iris.target
X = iris.data
print('鸢尾花的种类',iris.target_names)
print('数据的维度',X.shape)
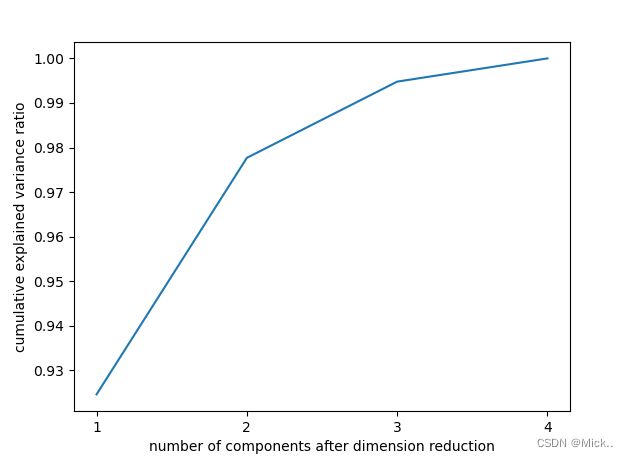
# 选择最好的n_components:累积可解释方差贡献率曲线
# 累积可解释方差贡献率曲线是一条以降维后保留的特征个数为横坐标,降维后新特征矩阵捕捉到的可解释方差贡献率为纵坐标的曲线,能够帮助我们决定n_components最好的取值
pca=PCA().fit(X)
plt.plot([1,2,3,4],np.cumsum(pca.explained_variance_ratio_))
plt.xticks([1,2,3,4]) #这是为了限制坐标轴显示为整数
plt.xlabel('number of components after dimension reduction')
plt.ylabel('cumulative explained variance ratio')
plt.show()
按信息量占比选超参数
import matplotlib.pyplot as plt
#导入鸢尾花数据集
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
import numpy as np
#2.提取数据集
iris = load_iris()
y = iris.target
X = iris.data
print('鸢尾花的种类',iris.target_names)
print('数据的维度',X.shape)
pca = PCA(n_components=0.93) #实例化
pca = pca.fit(X) #拟合模型
X_dr = pca.transform(X) #获取新矩阵
print('降维后数据的维度',X_dr.shape)
#属性explained_variance_,查看降维后每个新特征向量上所带的信息量大小(可解释性方差的大小)
print('查看降维后每个新特征向量上所带的信息量大小',pca.explained_variance_)
# 属性explained_variance_ratio_,查看降维后每个新特征向量所占的信息量占原始数据总信息量的百分比 .又叫做可解释方差贡献率
print('查看降维后每个新特征向量所占的信息量占原始数据总信息量的百分比',pca.explained_variance_ratio_)
#整个降维后的特征向量所带的所有信息在原始总信息量上的占比。
print('降维后的特征向量所带的所有信息在原始总信息量上的占比',pca.explained_variance_ratio_.sum())人脸图像的降维
import matplotlib.pyplot as plt
#fetch_lfw_people数据为7个人的1000多张照片组成的人脸数据
from sklearn.datasets import fetch_lfw_people
from sklearn.decomposition import PCA
import numpy as np
#2.提取数据集
#min_faces_per_person=60每个人最少需要的脸图
faces = fetch_lfw_people(min_faces_per_person=20)
y = faces.target
X = faces.data
print('人脸的类别',faces.target_names)
#原始数据的可视化
for i in range(1,21):
plt.subplot(4,5,i)
data=X[i]
image=data.reshape(62,47)
plt.imshow(image,cmap='gray')
plt.show()
print('数据的维度',X.shape)
pca = PCA(n_components=196) #实例化
pca = pca.fit(X) #拟合模型
X_dr = pca.transform(X) #获取新矩阵
print('降维后数据的维度',X_dr.shape)
V = pca.components_
print('新特征空间',V.shape)
x1=np.dot(X,V[:196,:].T)
print('手工降维',x1.shape)
print('判断手工降维和Pca降维',x1==X_dr)
##新特征空间可视化
for i in range(1,21):
plt.subplot(4,5,i)
data=V[i]
image=data.reshape(62,47)
plt.imshow(image,cmap='gray')
plt.show()
#属性explained_variance_,查看降维后每个新特征向量上所带的信息量大小(可解释性方差的大小)
print('查看降维后每个新特征向量上所带的信息量大小',pca.explained_variance_)
# 属性explained_variance_ratio_,查看降维后每个新特征向量所占的信息量占原始数据总信息量的百分比 .又叫做可解释方差贡献率
print('查看降维后每个新特征向量所占的信息量占原始数据总信息量的百分比',pca.explained_variance_ratio_)
#整个降维后的特征向量所带的所有信息在原始总信息量上的占比。
print('降维后的特征向量所带的所有信息在原始总信息量上的占比',pca.explained_variance_ratio_.sum())inverse_transform 实现图像的降噪
降维的目的之一就是希望抛弃掉对模型带来负面影响的特征,而我们相信,带有效信息的特征的方差应该是远大于噪音的,所以相比噪音,有效的特征所带的信息应该不会在PCA过程中被大量抛弃。inverse_transform能够在不恢复原始数据的情况下,将降维后的数据返回到原本的高维空间,即是说能够实现”保证维度,但去掉方差很小特征所带的信息“。
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
import numpy as np
from sklearn.datasets import load_digits
rng = np.random.RandomState(1218)
digits = load_digits()
data=digits.data
label=digits.target
print('数据的维度',data.shape)
print('数据的类别',set(digits.target.tolist()))
# 原始数据的可视化
for i in range(1,21):
plt.subplot(4,5,i)
image=data[i].reshape(8,8)
plt.imshow(image,cmap='gray')
plt.show()
noisy = np.random.normal(0,2,data.shape)
print(noisy.mean())
print(noisy.std())
noisy=data+noisy
#噪声数据可视化
for i in range(1,21):
plt.subplot(4,5,i)
image=noisy[i].reshape(8,8)
plt.imshow(image,cmap='gray')
plt.show()
#模型实例化并拟合
pca=PCA(0.9,svd_solver='full').fit(noisy)
X_dr=pca.transform(noisy)
print('降维后的维度',X_dr.shape)
# 逆转降维结果,实现降噪
data=pca.inverse_transform(X_dr)
print('逆转后的结果',data.shape)
#降噪后的结果可视化
for i in range(1,21):
plt.subplot(4,5,i)
image=noisy[i].reshape(8,8)
plt.imshow(image,cmap='gray')
plt.show()
#属性explained_variance_,查看降维后每个新特征向量上所带的信息量大小(可解释性方差的大小)
print('查看降维后每个新特征向量上所带的信息量大小',pca.explained_variance_)
# 属性explained_variance_ratio_,查看降维后每个新特征向量所占的信息量占原始数据总信息量的百分比 .又叫做可解释方差贡献率
print('查看降维后每个新特征向量所占的信息量占原始数据总信息量的百分比',pca.explained_variance_ratio_)
#整个降维后的特征向量所带的所有信息在原始总信息量上的占比。
print('降维后的特征向量所带的所有信息在原始总信息量上的占比',pca.explained_variance_ratio_.sum())参考文献
【机器学习】降维——PCA(非常详细) - 知乎 (zhihu.com)
机器学习-Sklearn-04(降维算法PCA和SVD)_Henrik698的博客-CSDN博客_explained_variance_ratio_