机器学习算法基础 5 线回归与岭回归
线性回归
线性回归的定义
回归问题的判定?
- 目标值连续
线性回归定义?
- 通过一个或者多个自变量与因变量之间之间进行建模的回归分析。其中特点为一个或多个称为回归系数的模型参数的线性组合,通俗理解,就是属性与权重的线性组合。通俗理解,就是属性与权重的线性组合
- 一元线性回归:涉及到的变量只有一个
- 多元线性回归:涉及到的变量两个或两个以上
y = k x + b y = kx + b y=kx+b
其中, b b b 偏置是为了单个特征的情况更加适用。
一个通过属性的线性组合来进行预测的函数:
f ( x ) = w 1 x 1 + w 2 x 2 + . . . + w d x d + b f(x) = w_1x_1 + w_2x_2 + ... + w_dx_d + b f(x)=w1x1+w2x2+...+wdxd+b
其中, w w w 为权重, b = w 0 × 1 b=w_0 \times 1 b=w0×1 称为偏置项。
预测函数(拟合函数)通用公式:
h ( w ) = w T x h(w) = w^T x h(w)=wTx
其中
w = ( w 0 w 1 w 2 . . . ) w = \begin{pmatrix} w_0 \\ w_1 \\ w_2 \\ ... \end{pmatrix} w=⎝⎜⎜⎛w0w1w2...⎠⎟⎟⎞
x = ( 1 x 1 x 2 . . . ) x = \begin{pmatrix} 1 \\ x_1 \\ x_2 \\ ... \end{pmatrix} x=⎝⎜⎜⎛1x1x2...⎠⎟⎟⎞
最小二乘法(损失函数)
预测结果与真实值的误差大小。如误差的平方和,既最小二乘法:
J ( w ) = ∑ i = 1 m ( h w ( x i ) − y i ) 2 J(w) = \displaystyle\sum_{i=1}^m(h_w(x_i) - y_i)^2 J(w)=i=1∑m(hw(xi)−yi)2
其中 J ( w ) J(w) J(w) 为关于参数 w w w 的损失函数, y i y_i yi 为第 i i i 个训练样本的真实值, h w ( x i ) h_w(x_i) hw(xi) 为第 i i i 个训练样本特征值组合预测函数
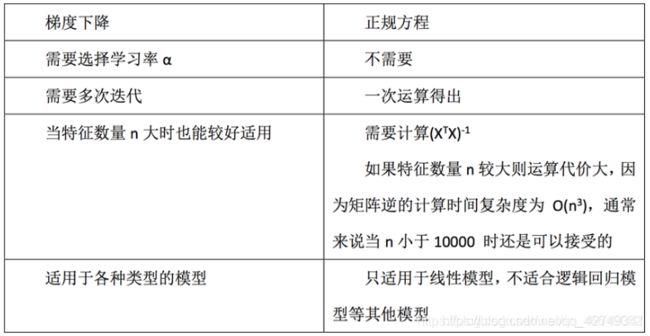
正规方程
找到最小损失对应的 W W W 值,数学原理简单。
w = ( X T X ) − 1 X T y w = (X^TX)^{-1}X^Ty w=(XTX)−1XTy
其中 X X X 为特征值矩阵, y y y 为目标值矩阵
缺点:
- 当特征过于复杂,求解慢
- 对于复杂的算法,不能使用正规方程求解(逻辑回归等)
梯度下降
首先我们给 θ θ θ 一个初试值,然后向着让 J ( θ ) J(θ) J(θ) 变化最大的方向更新 θ θ θ 的取值,如此迭代。公式如下:
θ j : = θ j − α ∂ ∂ θ j J ( θ ) \theta_j := \theta_j - \alpha \frac{\partial}{\partial\theta_j}J(\theta) θj:=θj−α∂θj∂J(θ)
其中 α \alpha α 为学习速率,需要手工指定
适用场景:训练馆数据规模庞大的任务。
https://blog.51cto.com/u_15075523/2583406
https://www.cntofu.com/book/85/math/analytic/least-square.md
https://www.cnblogs.com/BYRans/p/4700202.html
sklearn vs tensorflow
sklearn优点与缺点:
- 优点:封装好,建立模型简单、预测简单
- 缺点:看不到算法的过程,有些参数在算法API内部已经优化好了
tensorflow: 封装高低,很多东西可以自己指定
线性回归案例
# 线性回归案例-波士顿房价数据集分析
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, SGDRegressor
from sklearn.metrics import mean_squared_error
# 一、获得数据
lb = load_boston()
# 二、处理数据
# 1.取得数据集中特征值与目标值
x = lb.data
y = lb.target
# 2.分割数据集 训练集与测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25)
# 三、进行特征工程
# 1.训练集与测试集标准化处理
# 特征值与目标值都必须进行标准化处理,实例化两个API,分别处理特征值与目标值
# 特征值
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.transform(x_test)
# 目标值
std_y = StandardScaler()
# 要求传入的y_train是二维数组,后面也一样,用reshape(-1,1)方法转换
y_train = std_y.fit_transform(y_train.reshape(-1, 1))
y_test = std_y.transform(y_test.reshape(-1, 1))
# 四、线性回归模型-estimator预测
# 1.正规方程求解方式预测结果
lr = LinearRegression()
lr.fit(x_train, y_train)
print('正规方程回归系数为:\n', lr.coef_)
y_predict = std_y.inverse_transform(lr.predict(x_test))
print('正规方程预测测试集房子的价格:\n', y_predict)
print('正规方程预测与真实值均方误差:\n', mean_squared_error(y_test, y_predict))
# 2.梯度下降法对房价进行预测
sgd = SGDRegressor()
sgd.fit(x_train, y_train)
print('梯度下降法回归系数为:\n', sgd.coef_)
y_sgd_predict = std_y.inverse_transform(sgd.predict(x_test))
print('梯度下降法预测测试集房子的价格:\n', y_sgd_predict)
LinearRegression与SGDRegressor对比
结论:
- 线性回归器是最为简单、易用的回归模型。
- 从某种程度上限制了使用,尽管如此,在不知道特征之间关系的前提下,我们仍然使用线性回归器作为大多数系统的首要选择。
小规模数据:LinearRegression(不能解决过拟合问题)以及其它
大规模数据:SGDRegressor
过拟合与欠拟合
- 过拟合:一个假设在训练数据上能够获得比其他假设更好的拟合, 但是在训练数据外的数据集上却不能很好地拟合数据,此时认为这个假设出现了过拟合的现象。(模型过于复杂)
- 欠拟合:一个假设在训练数据上不能获得更好的拟合, 但是在训练数据外的数据集上也不能很好地拟合数据,此时认为这个假设出现了欠拟合的现象。(模型过于简单)
对线性模型进行训练学习会变成复杂模型。
模型变复杂的原因是数据的特征与目标值之间的关系不仅仅是线性关系。
欠拟合与过拟合原因以及解决办法
欠拟合原因以及解决办法
- 原因:学习到数据的特征过少
- 解决办法:增加数据的特征数量
过拟合原因以及解决办法
- 原因:原始特征过多,存在一些嘈杂特征,模型过于复杂是因为模型尝试去兼顾各个测试数据点
- 解决办法:
- 进行特征选择,消除关联性大的特征(很难做)
- 交叉验证(让所有数据都有过训练)
- 正则化(了解)
岭回归
正则化
L2 正则化:
作用:可以使得 W W W 的每个元素都很小,都接近于0,减少权重,尽量减小高次项特征的影响
优点:越小的参数说明模型越简单,越简单的模型则越不容易产生过拟合现象
Ridge:岭回归,带有正则化的线性回归,解决过拟合。
https://blog.csdn.net/google19890102/article/details/27228279
# 线性回归案例-波士顿房价数据集分析
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error
# 一、获得数据
lb = load_boston()
# 二、处理数据
# 1.取得数据集中特征值与目标值
x = lb.data
y = lb.target
# 2.分割数据集 训练集与测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25)
# 三、进行特征工程
# 1.训练集与测试集标准化处理
# 特征值与目标值都必须进行标准化处理,实例化两个API,分别处理特征值与目标值
# 特征值
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.transform(x_test)
# 目标值
std_y = StandardScaler()
# 要求传入的y_train是二维数组,后面也一样,用reshape(-1,1)方法转换
y_train = std_y.fit_transform(y_train.reshape(-1, 1))
y_test = std_y.transform(y_test.reshape(-1, 1))
# 四、线性回归模型-estimator预测
# 3.岭回归进行房价预测
rd = Ridge(alpha=1.0)
rd.fit(x_train, y_train)
# 回归系数
print('岭回归的回归系数为:\n', rd.coef_)
# 预测测试集房子价格
y_rd_predict = std_y.inverse_transform(rd.predict(x_test))
print('测试集房子价格为:\n', y_rd_predict)
# 回归性能评估
print('岭回归的回归性能评估为:', mean_squared_error(y_test, y_rd_predict))
# 4.岭回归交叉验证与网格搜索
rd_1 = Ridge()
param = {'alpha': [0.5, 1.0, 2]}
gc = GridSearchCV(rd_1, param_grid=param, cv=5)
gc.fit(x_train, y_train)
# 预测测试集房子价格
y_gc_predict = std_y.inverse_transform(gc.predict(x_test))
print('岭回归网格搜索的回归性能评估为:', mean_squared_error(y_test, y_gc_predict))
print('在交叉验证中最好的结果是:\n', gc.best_score_)
print('最好的参数选择是:\n', gc.best_params_)