【机器学习04】岭回归
4 岭回归
4.1 简介
普通线性回归模型使用基于梯度下降的最小二乘法,在最小化损失函数的前提下,寻找最优模型参数,在此过程中,包括少数异常样本在内的全部训练数据都会对最终模型参数造成程度相等的影响,异常值对模型所带来影响无法在训练过程中被识别出来
岭回归(Ridge回归):在模型迭代过程所依据的代价函数中增加了正则惩罚项(L2范数正则化),以限制模型参数对异常样本的匹配程度,进而提高模型面对多数正常样本的拟合精度,解决过拟合问题
正则化:
- 目的:防止过拟合
- 本质:约束(限制)要优化的模型参数
代价函数:
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∥ θ ∥ 2 2 = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n θ j 2 J(\theta)=\frac{1}{2m}\sum\limits_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2+\lambda \left\|\theta\right\|_2^2=\frac{1}{2m}\sum\limits_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2+\lambda\sum\limits_{j=1}^n\theta_j^{2} J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2+λ∥θ∥22=2m1i=1∑m(hθ(x(i))−y(i))2+λj=1∑nθj2
说明:λ>0
- L2范数:向量中的各个元素平方之和的开平方,即 ∥ θ ∥ 2 = ∑ j = 1 n θ j 2 {\left\| \theta \right\|_2} = \sqrt {\sum\limits_{j = 1}^n {\theta _j^2} } ∥θ∥2=j=1∑nθj2
- 正则强度λ(惩罚因子)越大,曲线的拟合度越低,忽略异常样本(噪音)的效果越好
4.2 梯度下降法(GD)
岭回归代价函数之梯度求解:
α J ( θ ) α θ j = α α θ j ( 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n θ j 2 ) \frac{\alpha J(\theta)}{\alpha \theta_j}=\frac{\alpha}{\alpha \theta_j}(\frac{1}{2m}\sum\limits_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2+\lambda\sum\limits_{j=1}^n\theta_j^{2}) αθjαJ(θ)=αθjα(2m1i=1∑m(hθ(x(i))−y(i))2+λj=1∑nθj2)
= 1 m ∑ i = 1 m [ ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) ] + λ α α θ j ( θ 1 2 + θ 2 2 + . . . + θ j 2 + . . . + θ n 2 ) =\frac{1}{m}{\sum\limits_{i=1}^m[(h_\theta(x^{(i)})-y^{(i)})}x_j^{(i)}]+\lambda\frac{\alpha}{\alpha \theta_j}(\theta_1^{2}+\theta_2^{2}+...+\theta_j^{2}+...+\theta_n^{2}) =m1i=1∑m[(hθ(x(i))−y(i))xj(i)]+λαθjα(θ12+θ22+...+θj2+...+θn2)
= 1 m ∑ i = 1 m [ ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) ] + 2 λ θ j =\frac{1}{m}{\sum\limits_{i=1}^m[(h_\theta(x^{(i)})-y^{(i)})}x_j^{(i)}]+2\lambda\theta_j =m1i=1∑m[(hθ(x(i))−y(i))xj(i)]+2λθj
梯度下降迭代公式——>更新模型参数θj
θ j = θ j − α α J ( θ ) α θ j = θ j − α ( 1 m ∑ i = 1 m [ ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) ] + 2 λ θ j ) \theta_j=\theta_j-\alpha\frac{\alpha J(\theta)}{\alpha \theta_j}=\theta_j-\alpha(\frac{1}{m}{\sum\limits_{i=1}^m[(h_\theta(x^{(i)})-y^{(i)})}x_j^{(i)}]+2\lambda\theta_j) θj=θj−ααθjαJ(θ)=θj−α(m1i=1∑m[(hθ(x(i))−y(i))xj(i)]+2λθj)
其中, h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n = ∑ i = 0 n θ i x i = θ T x , x 0 ( i ) = 1 h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+...+\theta_nx_n=\sum\limits_{i = 0}^n{{\theta_i}{x_i}}={\theta^T}x,x_0^{(i)}=1 hθ(x)=θ0+θ1x1+θ2x2+...+θnxn=i=0∑nθixi=θTx,x0(i)=1
4.3 Sklearn之岭回归
岭回归相关API:
# sklearn库
import sklearn.linear_model as lm
# 创建模型
model=lm.Ridge(正则强度,fit_intercept=是否训练截距,max_iter=最大迭代次数,normalize=是否特征归一化)
# 训练模型
# 输入:一个二维数组表示的样本矩阵
# 输出:每个样本最终的结果
model.fit(输入,输出)
# 预测输出
# 输入array是一个二维数组,每一行是一个样本,每一列是一个特征
result=model.predict(array)
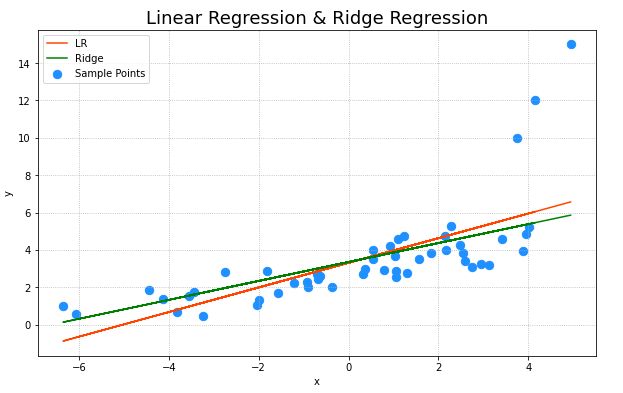
案例:加载abnormal.txt文件中的数据,基于岭回归算法训练回归模型
import numpy as np
import matplotlib.pyplot as plt
# sklearn库
import sklearn.linear_model as lm
import sklearn.metrics as sm
# 加载数据:读文本
def loaddata():
# x,y=np.loadtxt("data/abnormal.txt",delimiter=",",unpack=True)
data=np.loadtxt("data/abnormal.txt",delimiter=",")
cols=data.shape[1] # data.shape[1]:列数
x=data[:,0:cols-1]
y=data[:,-1].reshape(-1,1) # data[:,-1]:获取所有行的最后一列
return x,y
x,y=loaddata()
# 绘制散点图
plt.figure(figsize=(10,6))
plt.title("Linear Regression & Ridge Regression",fontsize=18)
plt.grid(linestyle=":")
# s:散点大小
plt.scatter(x,y,s=70,color="dodgerblue",label="Sample Points")
plt.xlabel("x")
plt.ylabel("y")
## 线性回归
model1=lm.LinearRegression()
model1.fit(x,y)
lr_pred_y=model1.predict(x)
plt.plot(x,lr_pred_y,color="orangered",label="LR")
# MAE(平均绝对值误差):1/mΣ|实际输出-预测输出|
print("MAE(平均绝对值误差):",sm.mean_absolute_error(y,lr_pred_y))
# MSE(均方误差):1/mΣ(实际输出-预测输出)^2
print("MSE(均方误差):",sm.mean_squared_error(y,lr_pred_y))
# RMSE(均方根误差):SQRT(1/mΣ(实际输出-预测输出)^2)
print("RMSE(均方根误差):",np.sqrt(sm.mean_squared_error(y,lr_pred_y)))
# R2_score(R方值):(0,1]区间的分值,即分数越高,误差越小
print("R2_score(R方值):",sm.r2_score(y,lr_pred_y))
## 岭回归
model2=lm.Ridge(0.3,fit_intercept=True,max_iter=1000,normalize=True) # 模型构建
model2.fit(x,y) # 模型训练
print("\n")
print("系数:",model2.coef_)
print("截距:",model2.intercept_)
ridge_pred_y=model2.predict(x)
plt.plot(x,ridge_pred_y,color="green",label="Ridge")
print("\n")
# MAE(平均绝对值误差):1/mΣ|实际输出-预测输出|
print("MAE(平均绝对值误差):",sm.mean_absolute_error(y,ridge_pred_y))
# MSE(均方误差):1/mΣ(实际输出-预测输出)^2
print("MSE(均方误差):",sm.mean_squared_error(y,ridge_pred_y))
# RMSE(均方根误差):SQRT(1/mΣ(实际输出-预测输出)^2)
print("RMSE(均方根误差):",np.sqrt(sm.mean_squared_error(y,ridge_pred_y)))
# R2_score(R方值):(0,1]区间的分值,即分数越高,误差越小
print("R2_score(R方值):",sm.r2_score(y,ridge_pred_y))
plt.legend()
plt.show()
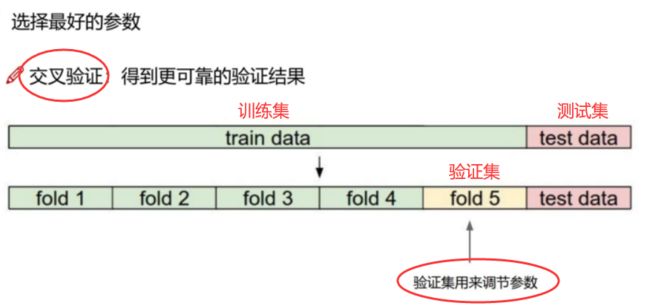
4.4 数据集划分与交叉验证
-
数据集划分
-
Training set(训练集): 训练模型
-
Validation set(验证集): 调整参数来选择模型,避免过拟合
-
Testing set(测试集): 评估模型
-
-
交叉验证(cross validation)
在机器学习模型中,需要人工选择的参数称为超参数
GridSearchCV(模型调参利器):包含GridSearch和CV,即网格搜索和交叉验证
GridSearch:一种调参手段,即穷举搜索:在所有候选的参数选择中,通过循环遍历,尝试每一种可能性,表现最好的参数就是最终的结果。这种方法的主要缺点是比较耗时!
所以网格搜索适用于三四个(或者更少)的超参数(当超参数的数量增长时,网格搜索的计算复杂度会呈现指数增长,这时候则使用随机搜索),用户列出一个较小的超参数值域,这些超参数值域的笛卡尔积(排列组合)为一组超参数。网格搜索算法使用每组超参数训练模型并挑选验证集误差最小的超参数组合
GridSearchCV的常用参数含义:模型调参利器(网格搜索与交叉验证)GridSearchCV参数详解
- estimator:选择使用的模型名
- param_grid: 需要最优化的参数取值,值为字典或者列表
- scoring:模型评价指标
- cv=k:k折交叉验证(训练集分成k份,其中1份为验证集),默认为3
4.5 Sklearn之模型保存与加载
模型训练是一个耗时的过程,一个优秀的机器学习模型是非常宝贵的
可以将模型保存到磁盘中,也可以在需要使用的时候从磁盘中重新加载模型即可,不需要重新训练,与训练好的模型具有相同的参数
模型保存与加载相关API:
# sklearn库
from sklearn.externals import joblib
joblib.dump(模型对象,磁盘文件) # 保存模型
model=joblib.load(磁盘文件) # 加载模型
案例:将训练好的模型保存到磁盘中
# sklearn库
from sklearn.externals import joblib
# 模型保存(将训练好的模型对象保存到磁盘文件中)
joblib.dump(model,"model/house_train_model.pkl")
# 模型加载(从磁盘文件中加载模型对象,与训练好的模型具有相同的参数)
model=joblib.load("model/house_train_model.pkl")
# 模型预测测试集数据输出
model.predict(X_test)
4.6 案例:波士顿房价预测
import numpy as np
import matplotlib.pyplot as plt
# sklearn库
from sklearn import linear_model
from sklearn.datasets import load_boston
# 获取数据
# 方式1:
# 加载sklearn库中自带的波士顿房价数据集
boston = load_boston()
# 查看数据集以及结构描述
print(boston.DESCR)
print(boston)
X = boston.data # 取特征值X
y = boston.target # 取标签y
# 方式2:
import pandas as pd
df = pd.read_excel('data/boston.xls')
print(df)
# 取特征值X
X = df[df.columns[0:-1]] # 切片:左闭右开,即第0列至倒数第2列数据
# 取标签y
y = df[df.columns[-1]] # 切片:最后一列数据
# 创建模型(定义岭回归)
model = linear_model.Ridge(alpha=0.1)
# 训练模型
model.fit(X,y)
# 模型预测
y_hat = model.predict(X)
# ---------------------- 训练模型(使用交叉验证选择合适的参数)------------------------
from sklearn.model_selection import train_test_split
# 划分训练集(70%)和测试集(30%)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
# GridSearchCV(模型调参利器):包含GridSearch和CV,即网格搜索和交叉验证
from sklearn.model_selection import GridSearchCV
# 创建模型(定义岭回归)
ridge_model = linear_model.Ridge()
# 参数字典(多次设置尝试)
param_test={'alpha':[0.01,0.03,0.05,0.07,0.1,0.5,0.8,1],'normalize':[True,False]}
# 定义模型调参(estimator:选择使用的模型名,param_grid:参数字典或列表,scoring:模型评价指标,cv=k:k折交叉验证)
gsearch = GridSearchCV(estimator=ridge_model, param_grid = param_test, scoring='neg_mean_squared_error', cv=5)
# 训练模型
gsearch.fit(X_train,y_train)
# 查看网格搜索和交叉验证的最好参数组合以及最好得分
print(gsearch.best_params_)
print(gsearch.best_score_)
# ---------------------------- 模型评估---------------------------
from sklearn.metrics import mean_squared_error
# 使用最好参数组合来创建模型(定义岭回归)
ridge_model = linear_model.Ridge(alpha=0.3,normalize=True)
# 训练模型
ridge_model.fit(X_train,y_train)
# 模型预测
# 训练集
y_train_pred = ridge_model.predict(X_train)
print('Train MSE=',mean_squared_error(y_train,y_train_pred))
# 测试集
y_test_pred = ridge_model.predict(X_test)
print('Test MSE=',mean_squared_error(y_test,y_test_pred))
#---------------------------- 模型部署使用 ------------------------
from sklearn.externals import joblib
# 模型保存
joblib.dump(ridge_model, "house_train_model.pkl")
# 模型加载
clf = joblib.load("house_train_model.pkl")
clf.predict(X_test)