基于轮廓系数来选择n_clusters(Kmeans聚类分析)
1、导库
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score
import matplotlib.pyplot as plt
import matplotlib.cm as cm # colormap
import numpy as np# 基于我们的轮廓系数来选择最佳的n_clusters
# 想要知道每个聚出来的类的轮廓系数是多少,还想要一个各个类之间的轮廓系数的对比
# 想知道聚类完毕之后图像的分布是什么模样
2、创建数据
# 创建数据,make_blobs的用法可参考之前的一篇博客。
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=500,n_features=2,centers=4,random_state=1)3、将函数包装,选取最佳n_clusters
for n_clusters in [2,3,4,5,6,7]:
# 先设定我们要分成的蔟数
n_clusters = n_clusters
# 创建一个画布,画布上共有一行两列两个图
fig, (ax1, ax2) = plt.subplots(1, 2)
# 画布尺寸,两个子图宽度共18,高度为7
fig.set_size_inches(18, 7)
# 第一图是我们的轮廓系数图像,是由各个蔟的轮廓系数组成的横向条形图
# 横向条形图的横坐标是我们的轮廓系数取值,横坐标是我们的每个样本,因为轮廓系数是对每一个样本进行计算的
# 首先要来设定横坐标
# 轮廓系数的取值在【-1,1】,但我们至少希望轮廓系数是大于0的
# 太长的横坐标不利于我们的可视化,所以只设定x的取值范围在[-0.1,1]之间
ax1.set_xlim([-0.1, 1]) # 设置横坐标
# 接下来就是设定纵坐标,通常来说,纵坐标是从0开始,最大取值到X.shape[0]的取值
# 但我们希望,每个蔟都能排在一起,不同的蔟之间有一定的空隙
# 以便观察不同的条形图聚成的块,理解它对应了哪一个蔟
# 因此,我们在设定纵坐标的取值范围的时候,在X.shape[0]上,加上一个距离(n_clusters + 1) * 10,留作间隔用。
ax1.set_ylim([0, X.shape[0] + (n_clusters + 1) * 10])
# 开始建模,调用聚类好的标签
clusterer = KMeans(n_clusters=n_clusters, random_state=10).fit(X)
cluster_labels = clusterer.labels_
# 调用轮廓系数分数,silhouette_score生成的是所有样本点的轮廓系数均值
# 两个需要输入的参数是,特征矩阵X和聚类完毕后的标签
silhouette_avg = silhouette_score(X, cluster_labels)
# 用print来报一下结果,现在的蔟数量下,整体的轮廓系数究竟有多少
print("For n_clusters =", n_clusters,
"The average silhouette_score is :", silhouette_avg)
# 调用silhouette_samples,返回每个样本下的轮廓系数,这就是我们的横坐标。
sample_silhouette_values = silhouette_samples(X, cluster_labels)
# 首先设定y轴上的初始取值
y_lower = 10
# 接下来,对每一个蔟进行循环
for i in range(n_clusters):
# 从样本的轮廓系数结果中抽取出第i个蔟的轮廓系数,并对他进行排序
ith_cluster_silhouette_values = sample_silhouette_values[cluster_labels == i]
# .sort()这个命令会直接改掉原数据的顺序
ith_cluster_silhouette_values.sort()
# 查看一个蔟中究竟有多少个样本
size_cluster_i = ith_cluster_silhouette_values.shape[0]
# 这一个蔟在y轴上的取值,应该是由初始值(y_lower)开始,到初始值加上这个蔟中的样本数量结束(y_upper)
y_upper = y_lower + size_cluster_i
# colormap库中,使用小数来调用颜色的函数
# 在nipy_spectral([输入任意小数代表一个颜色])
# 在我们希望看到的每个蔟的颜色是不同的,我们需要的颜色种类刚好是循环的个数的种类
# 只要能够确保,每次循环生成的小数是不同的,可以使用任意方式来获取小数
# 可以用i的浮点数除以n_clusters,在不同的i下,自然生成不同的小数
# 以确保所有的蔟会有不同的颜色
color = cm.nipy_spectral(float(i)/n_clusters)
#开始填充子图1中的内容
# fill_between是让一个范围中的柱状图都统一颜色的函数
# fill_betweenx的范围是在纵坐标上
# fill_betweeny 的范围是在横坐标上
# fill_betweenx的参数应该输入(纵坐标的下限,纵坐标的上限,X轴上的取值,柱状图的颜色)
ax1.fill_betweenx(np.arange(y_lower, y_upper)
,ith_cluster_silhouette_values
,facecolor=color
,alpha=0.7
)
# 为每个蔟的轮廓系数写上蔟的编号,并且让蔟的编号显示横坐标上每个条形图的中间位置
# text 的参数为(要显示编号的位置的横坐标,要显示标号位置的纵坐标,要显示的标号内容)
ax1.text(-0.05
, y_lower + 0.5 * size_cluster_i
, str(i))
# 为下一个蔟计算新的y轴上的初始值,是每一次迭代之后,y的上限再加上10
# 以此来保证,不同的蔟的图像之间显示有空隙
y_lower = y_upper + 10
#给图1加上标题,横坐标轴,纵坐标轴的标签
ax1.set_title("The silhouette plot for the various clusters.")
ax1.set_xlabel("The silhouette coefficient values")
ax1.set_ylabel("Cluster label")
# 把整个数据集上的轮廓系数的均值以虚线的形式放入我们的图中
ax1.axvline(x=silhouette_avg, color="red", linestyle="--")
# 让y轴上不显示任何刻度
ax1.set_yticks([])
# 让X轴上的刻度显示为我们规定的刻度
ax1.set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])
# 开始对第二个图进行处理,首先获取新颜色,由于这里没有循环,因此,我们需要一次性生成多个小数来获取多个颜色
# cluster_labels.astype(float)是指将整数转为浮点数
colors = cm.nipy_spectral(cluster_labels.astype(float) / n_clusters)
ax2.scatter(X[:, 0], X[:, 1]
,marker='o' # 点的形状
,s=8 # 点的大小
,c=colors
)
# 把生成的质心放到图像中去
centers = clusterer.cluster_centers_
# Draw white circles at cluster centers
ax2.scatter(centers[:, 0], centers[:, 1], marker='x',
c="red", alpha=1, s=200)
# 为图二设置标题,横坐标标题,纵坐标标题
ax2.set_title("The visualization of the clustered data.")
ax2.set_xlabel("Feature space for the 1st feature")
ax2.set_ylabel("Feature space for the 2nd feature")
# 为整个图设置标题
plt.suptitle(("Silhouette analysis for KMeans clustering on sample data "
"with n_clusters = %d" % n_clusters),
fontsize=14, fontweight='bold')
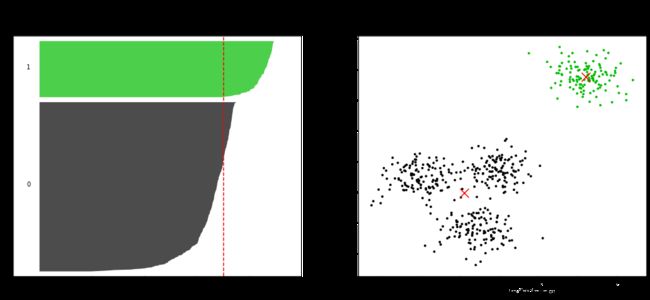
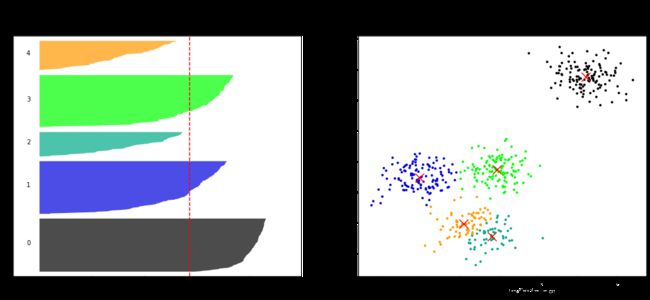
plt.show()显示的效果为:
For n_clusters = 2 The average silhouette_score is : 0.7049787496083262
For n_clusters = 3 The average silhouette_score is : 0.5882004012129721
For n_clusters = 4 The average silhouette_score is : 0.6505186632729437
For n_clusters = 5 The average silhouette_score is : 0.5745566973301872
For n_clusters = 6 The average silhouette_score is : 0.4387644975296138
For n_clusters = 7 The average silhouette_score is : 0.3728615111052894
从上面的结果中,可以看出,当n_clusters=2或4时,聚类效果最好。可以根据业务需求,选择适合的分类个数。