机器学习-sklearn第七天——笔记

sklearn中的聚类算法K-Means

1 概述

1.1 无监督学习与聚类算法

聚类算法又叫做“无监督分类”，其目的是将数据划分成有意义或有用的组（或簇）。这种划分可以基于我们的业务需求或建模需求来完成，也可以单纯地帮助我们探索数据的自然结构和分布。比如在商业中，如果我们手头有大量的当前和潜在客户的信息，我们可以使用聚类将客户划分为若干组，以便进一步分析和开展营销活动，最有名的客户价值判断模型RFM，就常常和聚类分析共同使用。再比如，聚类可以用于降维和矢量量化（vectorquantization），可以将高维特征压缩到一列当中，常常用于图像，声音，视频等非结构化数据，可以大幅度压缩数据量。

1.2 sklearn中的聚类算法

聚类算法在sklearn中有两种表现形式，一种是类（和我们目前为止学过的分类算法以及数据预处理方法们都一样），需要实例化，训练并使用接口和属性来调用结果。另一种是函数（function），只需要输入特征矩阵和超参数，即可返回聚类的结果和各种指标。

2 KMeans

2.1 KMeans是如何工作的

关键概念：簇与质心
KMeans算法将一组N个样本的特征矩阵X划分为K个无交集的簇，直观上来看是簇是一组一组聚集在一起的数据，在一个簇中的数据就认为是同一类。簇就是聚类的结果表现。簇中所有数据的均值 通常被称为这个簇的“质心”（centroids）。在一个二维平面中，一簇数据点的质心的横坐标就是这一簇数据点的横坐标的均值，质心的纵坐标就是这一簇数据点的纵坐标的均值。同理可推广至高维空间。
在KMeans算法中，簇的个数K是一个超参数，需要我们人为输入来确定。KMeans的核心任务就是根据我们设定好
的K，找出K个最优的质心，并将离这些质心最近的数据分别分配到这些质心代表的簇中去。具体过程可以总结如下：

那什么情况下，质心的位置会不再变化呢？当我们找到一个质心，在每次迭代中被分配到这个质心上的样本都是一致的，即每次新生成的簇都是一致的，所有的样本点都不会再从一个簇转移到另一个簇，质心就不会变化了。

2.2 簇内误差平方和的定义和解惑

聚类算法聚出的类有什么含义呢？这些类有什么样的性质？我们认为，被分在同一个簇中的数据是有相似性的，而不同簇中的数据是不同的，当聚类完毕之后，我们就要分别去研究每个簇中的样本都有什么样的性质，从而根据业务需求制定不同的商业或者科技策略。这个听上去和我们在上周的评分卡案例中讲解的“分箱”概念有些类似，即我们分箱的目的是希望，一个箱内的人有着相似的信用风险，而不同箱的人的信用风险差异巨大，以此来区别不同信用度的人，因此我们追求“组内差异小，组间差异大”。聚类算法也是同样的目的，我们追求“簇内差异小，簇外差异大”。而这个“差异“，由样本点到其所在簇的质心的距离来衡量。

解惑：Kmeans有损失函数吗？
记得我们在逻辑回归中曾有这样的结论：损失函数本质是用来衡量模型的拟合效果的，只有有着求解参数需求的算法，才会有损失函数。Kmeans不求解什么参数，它的模型本质也没有在拟合数据，而是在对数据进行一种探索。所以如果你去问大多数数据挖掘工程师，甚至是算法工程师，他们可能会告诉你说，K-Means不存在什么损失函数，Inertia更像是Kmeans的模型评估指标，而非损失函数。
但我们类比过了Kmeans中的Inertia和逻辑回归中的损失函数的功能，我们发现它们确实非常相似。所以，从“求解模型中的某种信息，用于后续模型的使用“这样的功能来看，我们可以认为Inertia是Kmeans中的损失函数，虽然这种说法并不严谨。
对比来看，在决策树中，我们有衡量分类效果的指标准确度accuracy，准确度所对应的损失叫做泛化误差，但我们不能通过最小化泛化误差来求解某个模型中需要的信息，我们只是希望模型的效果上表现出来的泛化误差很小。因此决策树，KNN等算法，是绝对没有损失函数的。

2.3 KMeans算法的时间复杂度

3 sklearn.cluster.KMeans

class sklearn.cluster.KMeans (n_clusters=8, init=’k-means++’, n_init=10, max_iter=300, tol=0.0001,
precompute_distances=’auto’, verbose=0, random_state=None, copy_x=True, n_jobs=None, algorithm=’auto’)

3.1 重要参数n_clusters

n_clusters是KMeans中的k，表示着我们告诉模型我们要分几类。这是KMeans当中唯一一个必填的参数，默认为8类，但通常我们的聚类结果会是一个小于8的结果。通常，在开始聚类之前，我们并不知道n_clusters究竟是多少，因此我们要对它进行探索。

3.1.1 先进行一次聚类看看吧

当我们拿到一个数据集，如果可能的话，我们希望能够通过绘图先观察一下这个数据集的数据分布，以此来为我们聚类时输入的n_clusters做一个参考。
首先，我们来自己创建一个数据集。这样的数据集是我们自己创建，所以是有标签的。

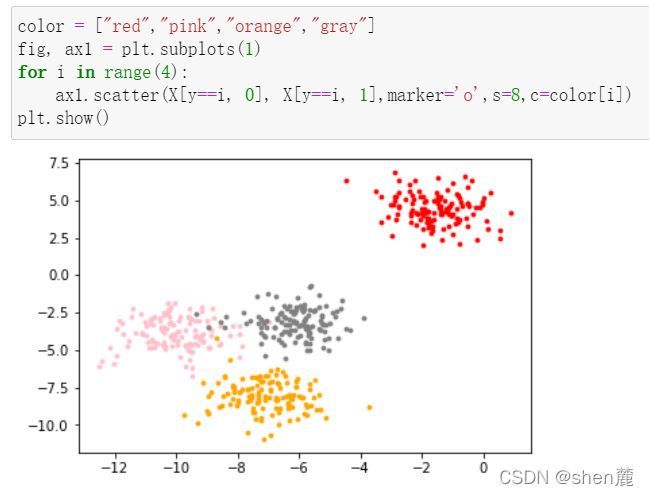
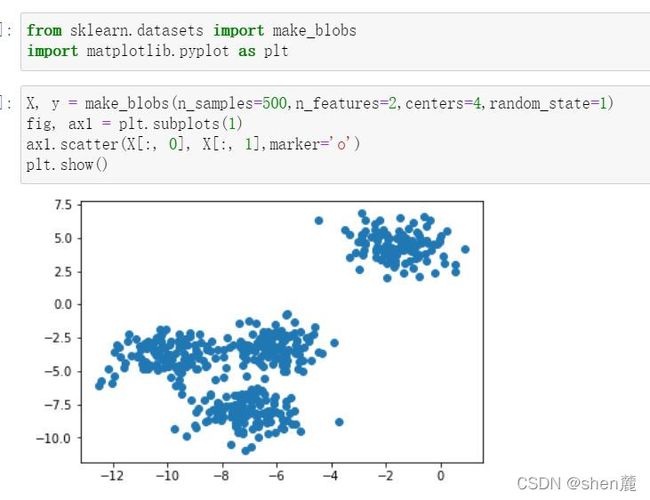
基于这个分布，我们来使用Kmeans进行聚类。首先，我们要猜测一下，这个数据中有几簇？

3.1.2 聚类算法的模型评估指标

不同于分类模型和回归，聚类算法的模型评估不是一件简单的事。在分类中，有直接结果（标签）的输出，并且分类的结果有正误之分，所以我们使用预测的准确度，混淆矩阵，ROC曲线等等指标来进行评估，但无论如何评估，都是在”模型找到正确答案“的能力。而回归中，由于要拟合数据，我们有SSE均方误差，有损失函数来衡量模型的拟合程度。但这些衡量指标都不能够使用于聚类。

面试高危问题：如何衡量聚类算法的效果？
聚类模型的结果不是某种标签输出，并且聚类的结果是不确定的，其优劣由业务需求或者算法需求来决定，并且没有永远的正确答案。那我们如何衡量聚类的效果呢？

记得我们说过，KMeans的目标是确保“簇内差异小，簇外差异大”，我们就可以通过衡量簇内差异来衡量聚类的效果。我们刚才说过，Inertia是用距离来衡量簇内差异的指标，因此，我们是否可以使用Inertia来作为聚类的衡量指标呢？Inertia越小模型越好嘛。
可以，但是这个指标的缺点和极限太大。
首先，它不是有界的。我们只知道，Inertia是越小越好，是0最好，但我们不知道，一个较小的Inertia究竟有没有达到模型的极限，能否继续提高。
第二，它的计算太容易受到特征数目的影响，数据维度很大的时候，Inertia的计算量会陷入维度诅咒之中，计算量会爆炸，不适合用来一次次评估模型。
第三，它会受到超参数K的影响，在我们之前的常识中其实我们已经发现，随着K越大，Inertia注定会越来越小，但这并不代表模型的效果越来越好了
第四，Inertia对数据的分布有假设，它假设数据满足凸分布（即数据在二维平面图像上看起来是一个凸函数的样子），并且它假设数据是各向同性的（isotropic），即是说数据的属性在不同方向上代表着相同的含义。但是现实中的数据往往不是这样。所以使用Inertia作为评估指标，会让聚类算法在一些细长簇，环形簇，或者不规则形状的
流形时表现不佳

3.1.2.1 当真实标签已知的时候

虽然我们在聚类中不输入真实标签，但这不代表我们拥有的数据中一定不具有真实标签，或者一定没有任何参考信息。当然，在现实中，拥有真实标签的情况非常少见（几乎是不可能的）。如果拥有真实标签，我们更倾向于使用分类算法。但不排除我们依然可能使用聚类算法的可能性。如果我们有样本真实聚类情况的数据，我们可以对于聚类算法的结果和真实结果来衡量聚类的效果。

3.1.2.2 当真实标签未知的时候：轮廓系数

在99%的情况下，我们是对没有真实标签的数据进行探索，也就是对不知道真正答案的数据进行聚类。这样的聚类，是完全依赖于评价簇内的稠密程度（簇内差异小）和簇间的离散程度（簇外差异大）来评估聚类的效果。其中轮廓系数是最常用的聚类算法的评价指标。它是对每个样本来定义的，它能够同时衡量：
1）样本与其自身所在的簇中的其他样本的相似度a，等于样本与同一簇中所有其他点之间的平均距离
2）样本与其他簇中的样本的相似度b，等于样本与下一个最近的簇中的所有点之间的平均距离

我们来看看轮廓系数在我们自建的数据集上表现如何

3.1.2.3 当真实标签未知的时候：Calinski-Harabaz Index

除了轮廓系数是最常用的，我们还有卡林斯基-哈拉巴斯指数（Calinski-Harabaz Index，简称CHI，也被称为方差
比标准），戴维斯-布尔丁指数（Davies-Bouldin）以及权变矩阵（Contingency Matrix）可以使用。

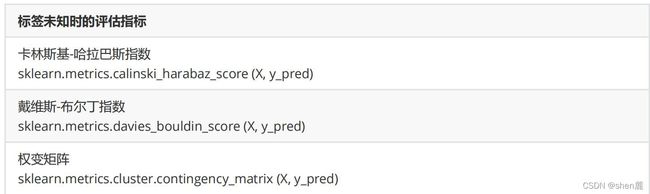
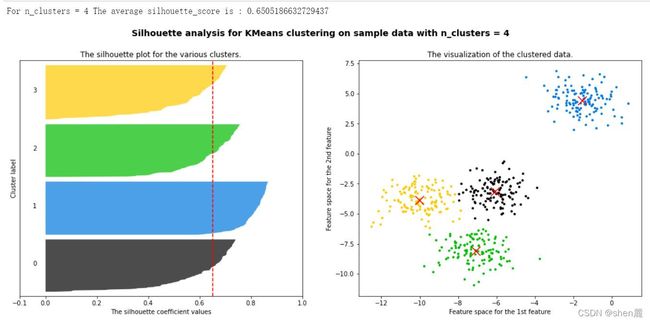
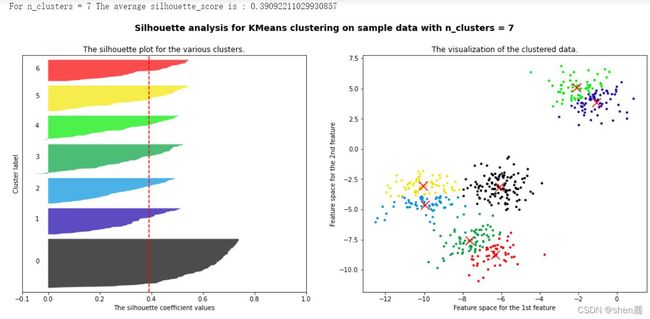
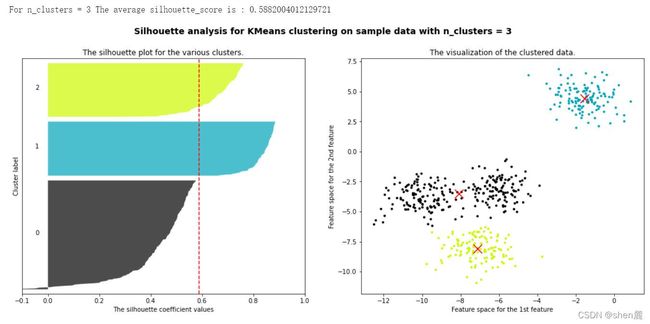
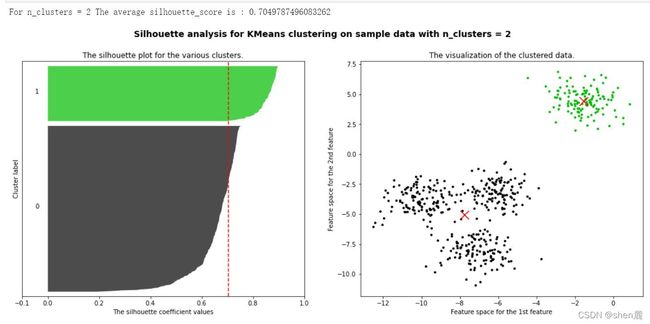
3.1.3 案例：基于轮廓系数来选择n_clusters

我们通常会绘制轮廓系数分布图和聚类后的数据分布图来选择我们的最佳n_clusters。

from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
n_clusters = 4
fig, (ax1, ax2) = plt.subplots(1, 2)
fig.set_size_inches(18, 7)
ax1.set_xlim([-0.1, 1])
ax1.set_ylim([0, X.shape[0] + (n_clusters + 1) * 10])
clusterer = KMeans(n_clusters=n_clusters, random_state=10).fit(X)
cluster_labels = clusterer.labels_
silhouette_avg = silhouette_score(X, cluster_labels)
print("For n_clusters =", n_clusters,"The average silhouette_score is :", silhouette_avg)
sample_silhouette_values = silhouette_samples(X, cluster_labels)
y_lower = 10
for i in range(n_clusters):
    ith_cluster_silhouette_values = sample_silhouette_values[cluster_labels == i]
    ith_cluster_silhouette_values.sort()
    size_cluster_i = ith_cluster_silhouette_values.shape[0]
    y_upper = y_lower + size_cluster_i
    color = cm.nipy_spectral(float(i)/n_clusters)
    ax1.fill_betweenx(np.arange(y_lower, y_upper)
                      ,ith_cluster_silhouette_values
                      ,facecolor=color
                      ,alpha=0.7
                     )
    ax1.text(-0.05
             , y_lower + 0.5 * size_cluster_i
             , str(i))
    y_lower = y_upper + 10
ax1.set_title("The silhouette plot for the various clusters.")
ax1.set_xlabel("The silhouette coefficient values")
ax1.set_ylabel("Cluster label")
ax1.axvline(x=silhouette_avg, color="red", linestyle="--")
ax1.set_yticks([])
ax1.set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])
colors = cm.nipy_spectral(cluster_labels.astype(float) / n_clusters)
ax2.scatter(X[:, 0], X[:, 1]
            ,marker='o'
            ,s=8
            ,c=colors
           )
centers = clusterer.cluster_centers_
ax2.scatter(centers[:, 0], centers[:, 1], marker='x',c="red", alpha=1, s=200)
ax2.set_title("The visualization of the clustered data.")
ax2.set_xlabel("Feature space for the 1st feature")
ax2.set_ylabel("Feature space for the 2nd feature")
plt.suptitle(("Silhouette analysis for KMeans clustering on sample data "
              "with n_clusters = %d" % n_clusters),
             fontsize=14, fontweight='bold')
plt.show()

将上述过程包装成一个循环，可以得到：

from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
for n_clusters in [2,3,4,5,6,7]:
    n_clusters = n_clusters
    fig, (ax1, ax2) = plt.subplots(1, 2)
    fig.set_size_inches(18, 7)
    ax1.set_xlim([-0.1, 1])
    ax1.set_ylim([0, X.shape[0] + (n_clusters + 1) * 10])
    clusterer = KMeans(n_clusters=n_clusters, random_state=10).fit(X)
    cluster_labels = clusterer.labels_
    silhouette_avg = silhouette_score(X, cluster_labels)
    print("For n_clusters =", n_clusters,
          "The average silhouette_score is :", silhouette_avg)
    sample_silhouette_values = silhouette_samples(X, cluster_labels)
    y_lower = 10
    for i in range(n_clusters):
        ith_cluster_silhouette_values = sample_silhouette_values[cluster_labels == i]
        ith_cluster_silhouette_values.sort()
        size_cluster_i = ith_cluster_silhouette_values.shape[0]
        y_upper = y_lower + size_cluster_i
        color = cm.nipy_spectral(float(i)/n_clusters)
        ax1.fill_betweenx(np.arange(y_lower, y_upper)
                          ,ith_cluster_silhouette_values
                          ,facecolor=color
                          ,alpha=0.7
                         )
        ax1.text(-0.05
                 , y_lower + 0.5 * size_cluster_i
                 , str(i))
        y_lower = y_upper + 10
    ax1.set_title("The silhouette plot for the various clusters.")
    ax1.set_xlabel("The silhouette coefficient values")
    ax1.set_ylabel("Cluster label")
    ax1.axvline(x=silhouette_avg, color="red", linestyle="--")
    ax1.set_yticks([])
    ax1.set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])
    colors = cm.nipy_spectral(cluster_labels.astype(float) / n_clusters)
    ax2.scatter(X[:, 0], X[:, 1]
                ,marker='o'
                ,s=8
                ,c=colors
               )
    centers = clusterer.cluster_centers_
    ax2.scatter(centers[:, 0], centers[:, 1], marker='x',
                c="red", alpha=1, s=200)
    ax2.set_title("The visualization of the clustered data.")
    ax2.set_xlabel("Feature space for the 1st feature")
    ax2.set_ylabel("Feature space for the 2nd feature")
    plt.suptitle(("Silhouette analysis for KMeans clustering on sample data "
                  "with n_clusters = %d" % n_clusters),
                 fontsize=14, fontweight='bold')
    plt.show()

3.2 重要参数init & random_state & n_init：初始质心怎么放好?

init：可输入"k-means++"，“random"或者一个n维数组。这是初始化质心的方法，默认"k-means++”。输入"kmeans++"：一种为K均值聚类选择初始聚类中心的聪明的办法，以加速收敛。如果输入了n维数组，数组的形状应该是(n_clusters，n_features)并给出初始质心。
random_state：控制每次质心随机初始化的随机数种子n_init：整数，默认10，使用不同的质心随机初始化的种子来运行k-means算法的次数。最终结果会是基于Inertia来计算的n_init次连续运行后的最佳输出

3.3 重要参数max_iter & tol：让迭代停下来

在之前描述K-Means的基本流程时我们提到过，当质心不再移动，Kmeans算法就会停下来。但在完全收敛之前，我们也可以使用max_iter，最大迭代次数，或者tol，两次迭代间Inertia下降的量，这两个参数来让迭代提前停下来。有时候，当我们的n_clusters选择不符合数据的自然分布，或者我们为了业务需求，必须要填入与数据的自然分布不合的n_clusters，提前让迭代停下来反而能够提升模型的表现。
max_iter：整数，默认300，单次运行的k-means算法的最大迭代次数
tol：浮点数，默认1e-4，两次迭代间Inertia下降的量，如果两次迭代之间Inertia下降的值小于tol所设定的值，迭
代就会停下

3.4 重要属性与重要接口

3.5 函数cluster.k_means

sklearn.cluster.k_means (X, n_clusters, sample_weight=None, init=’k-means++’, precompute_distances=’auto’,
n_init=10, max_iter=300, verbose=False, tol=0.0001, random_state=None, copy_x=True, n_jobs=None,
algorithm=’auto’, return_n_iter=False)
函数k_means的用法其实和类非常相似，不过函数是输入一系列值，而直接返回结果。一次性地，函数k_means会依次返回质心，每个样本对应的簇的标签，inertia以及最佳迭代次数。

4 案例：聚类算法用于降维，KMeans的矢量量化应用

K-Means聚类最重要的应用之一是非结构数据（图像，声音）上的矢量量化（VQ）。非结构化数据往往占用比较多的储存空间，文件本身也会比较大，运算非常缓慢，我们希望能够在保证数据质量的前提下，尽量地缩小非结构化数据的大小，或者简化非结构化数据的结构。矢量量化就可以帮助我们实现这个目的。KMeans聚类的矢量量化
本质是一种降维运用，但它与我们之前学过的任何一种降维算法的思路都不相同。特征选择的降维是直接选取对模型贡献最大的特征，PCA的降维是聚合信息，而矢量量化的降维是在同等样本量上压缩信息的大小，即不改变特征的数目也不改变样本的数目，只改变在这些特征下的样本上的信息量。
用K-Means聚类中获得的质心来替代原有的数据，可以把数据上的信息量压缩到非常小，但又不损失太多信息。我们接下来就通过一张图图片的矢量量化来看一看K-Means如何实现压缩数据大小，却不损失太多信息量。

1. 导入需要的库

2. 导入数据，探索数据
   
   
   

3. 决定超参数，数据预处理
   

4. 对数据进行K-Means的矢量量化
   

5. 对数据进行随机的矢量量化
   

6. 将原图，按KMeans矢量量化和随机矢量量化的图像绘制出来