论文笔记----LINE: Large-scale Information Network Embedding（大规模信息网络嵌入）

论文链接：http://de.arxiv.org/pdf/1503.03578

论文简介

论文主要研究的问题是将大型信息网络嵌入到低维向量空间中（即降维，将原本的高维空间转变为一个低维子空间），这个问题在可视化、节点分类和链路预测等许多任务中都有用。

论文主要介绍了一种新的网络嵌入方法“LINE”，它适用于任意类型的信息网络：有向、无向及加权。

• 该方法优化了目标函数，同时保留了局部和全局网络结构。针对经典随机梯度下降算法的局限性，它提出了一种边缘采用算法，提高了预测的效果。文中提出了一个精心设计的目标函数，保持了一阶和二阶近似。

论文的主要成果

1.提出了一种新的网络嵌入模型，称为“LINE”，它适合于任意类型的信息网络，并且易于扩展到数百万个节点。它有一个精心设计的目标函数，既保持一阶接近又保持二阶接近。

2.提出了一种用于优化目标的边缘采样算法。该算法克服了经典随机梯度下降算法的局限性，提高了推理的有效性和效率。

3.在真实世界的信息网络上进行了广泛的实验。实验结果证明了该模型的有效性和有效性。

相关工作

论文工作涉及到一般的图嵌入和降维的方法，这些算法通常依赖于求解引力矩阵的前导特征向量，其复杂度与节点数目至少是二次的，这使得它们处理大规模网络的效率很低。
同时，论文的工作还与图分解技术和DeepWalk相关。

问题定义

文章利用一阶近似和二阶近似，正式定义了大规模信息网络嵌入的问题：

• 定义1.信息网络被定义为G = (V,E)，其中V是顶点集合，每个顶点表示数据对象；E是顶点之间边的集合，每个边e∈E是有序对e=(u，v)，并且与权重Wuv>0相关联，这表示关系的强度。本文中只考虑非负权值

• 定义2.（一阶接近度）网络中的一阶接近度是两个顶点之间的局部成对接近度。对于由边（u，v）链接的每对顶点，该边上的权重Wuv表示u和v之间的一阶近似。如果在u和v之间没有观察到边，则它们的一阶近似为0。一阶接近度通常表示现实网络中两个结点的相似性。仅靠一阶邻近度是不足以保持网络结构的，并且寻求解决稀疏性问题的替代邻近度概念是重要的。

• 定义3.（二阶近似）网络中一对顶点（u，v）之间的二阶近似是它们的邻域网络结构之间的相似性。数学上，让pu=(ω(u1),.…ω(u|v|))表示u与所有其它顶点的一阶接近度，然后u和v之间的二阶接近度由pu和pv之间的相似度决定。如果没有顶点连接u和v，则u和v之间的二阶接近度为0。

• 定义4.(大规模信息网络嵌入)给定一个大网络G=(V，E)，大规模信息网络嵌入问题旨在将每个顶点v∈V表示为低维空间Rd，即学习函数fG:V→Rd，其中d《|V|。在空间Rd中，保持顶点之间的一阶接近和二阶接近。

算法介绍

• LINE满足一下三个要求：
  1.保持顶点之间的一阶近似和二阶近似；
  2.它必须能够扩展到非常大的网络，比如数百万个顶点和数十亿条边；
  3.以处理任意边缘类型的网络:有向、无向和/或加权。

模型介绍

一阶近似的LINE模型：

一阶近似度是指网络中顶点之间的局部两两接近度。为了建模一阶近似度，对于每条无向边(i,j)，我们定义顶点vi和vj的联合概率如下：

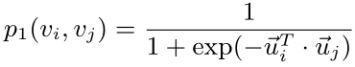
其中ui∈Rd是节点vi的低维向量空间表示，在空间V×V上定义一个分布p(,)，p(,)为经验概率定义为p(i,j) = wij/W ，其中W=∑(i,j)∈Eωij。为了保持一阶近似，一个简单的方法是最小化以下目标函数:

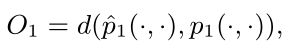
其中d( · , · )为两个分布之间的距离，一阶接近性只适用于无向图，而不适合有向图。

二阶近似的LINE模型：

二阶接近性既适用于有向图，也适用于无向图。二阶接近性假设有许多共享临接点的顶点彼此相似。每个顶点被视为特定的上下文，即假设在上下文上具有相似分别的顶点是相似的。每个顶点都扮演两个角色：顶点本身以及其他顶点的上下文；对于每个有向边(i,j)，我们将顶点vi生成上下文vj的概率定义为：

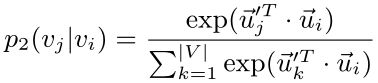
其中ui->是将ui视为顶点时的表示，而ui’->是将ui视为上下文时的表示；|V|是顶点或上下文时数量。

上式为一个条件分布，对于每一个vi，定义了上下文的条件分布p(·|vi)，降维后使其条件分布p(·|vi)接近其经验分布p^(·|vi)；因此最小化以下目标函数：

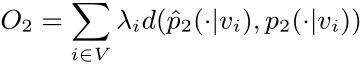
其中d(·,·)是两个分布之间的距离，经验分布p^{(·|vi)定义为经验分布p}(·|vi)=wij/di，其中wij是边(i,j)的权重，di是顶点i的出度。本文中将λi设置为顶点i的度，即λi=di，用KL-散度作为距离散度替代d(·,·)，并省略一些常数，有：

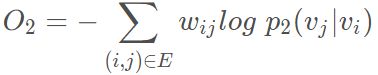
结合一阶和二阶近似：LINE模型保留了一阶近似和二阶近似，对嵌入进行串联，通过两种方法对每个顶点进行了训练。

模型优化

上述O2在计算条件概率p(·|vi)时，需要对整个顶点集求和，计算量较大；文章采用了负采样的方法来缓解这个问题，该方法根据每条边(i,j)的一些噪声分布对多个负采样边缘进行采样。也就是为每条边(i,j)指定以下目标函数：

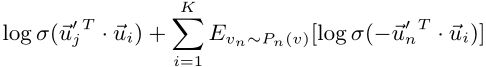
其中σ(x) = 1/(1 + exp(−x)) 是sigmoid函数，第一项是对观测到的边建模，第二项是对噪声分布中的负边建模；

• 文章采用异步随机梯度算法(ASGD) 对上述目标函数进行优化：在每一步中，ASGD算法都会对部分边样本进行采样，然后更新模型参数。

与此同时也会出现一个新的问题，如果根据小权重的边缘选择较大的学习率，那么大权重的边上的梯度就会爆炸式的过大，如果我们根据具有较大权重的边选择学习小的速率，那么小权重上的边的梯度将变得太小。因此边缘采样同样要优化。从起始边缘采样并将采样的边缘作为二进制边缘，其中采样概率与原始边缘的权重成比例。

实验

文章将LINE网络应用于几个不同类型的几个大型现实世界网络，包括语言网络，两个社交网络和两个引用网络。

数据集

(1)语言网络：整个英文维基百科页面构建了一个词共同网络
(2)社交网络：Flickr和Youtube
(3)引用网络：作者引文网和论文引文网

它们代表了各种各样的信息网络:有向的和无向的，二进制的和加权的。每个网络至少包含50万个节点和数百万条边，最大的网络包含约200万个节点和10亿条边。

文章并没有将LINE与MDS, IsoMap, Laplacian eiqenmap等经典图嵌入算法进行比较，因为这些算法无法处理这么大规模的网络。仅将LINE模型与几种可以扩展到非常大型网络的现有图形嵌入方法进行了比较。

定量结果

语言网络：使用了单词类比和文档分类两个应用程序来评估学习的嵌入有效性；其中词类比就是给定一个单词对（a,b）和一个单词c，该任务旨在找到一个单词d，使得c和d之间的关系类似于a和b之间的关系；其中文档分类可以用来评估文档表示，使用单词向量来计算文档表示，文章取文档中单词向量表示的平均值来获得文档向量；

社交网络：与语言网络相比，社交网络更加稀缺；将每个节点分配到一个或多个社区的多标签分类任务来评估顶点嵌入；随机抽取不同百分比的顶点进行训练，其余用于评估。结果在10次不同运行中进行平均。

引用网络：文章在两个引用网络上展示了结果，这两个网络都是有向网络，而GF和LINE方法虽然使用了一阶接近性，但它们都不适用于有向网络，因此只比较了DeepWalk和LINE2。文章还通过多标签分类任务评估顶点嵌入，选择7个流行会议，包括AAAI，CIKM，ICML，KDD，NIPS，SIGIR和WWW作为分类类别。

总结

• 本文提出的LINE有着很好的目标函数，同时保留了一阶近似和二阶近似；优化了目标函数，同时保留了局部和全局网络结构；针对经典随机梯度下降算法的局限性，它提出了一种边缘采用算法，提高了预测的效果。