关于疫情风险研判的传统模型以及扩展研究

关于疫情风险研判的传统模型以及扩展研究

        最近在看司守奎老师的《python数学实验与建模》一书，在完成课后习题的过程中，接触到到关于疫情预测的问题，要求对SIR模型进行改进。很有意思，尝试实现了一下，如有错误，皆可批评指正。

一、传统模型介绍

        SIR模型，只是一种简单的疫情预测模型，针对这种模型的改进也较多，最著名的便是SEIR模型。SEIR模型增加了一种人群类型，即暴露者（潜伏者）类型（E类），模型整体变化规律为：S-->E-->I-->R，（易感者-->潜伏者-->感染者-->免疫者）。假设人群变化除了递进以及结束，其它互不影响，不存在环状交替。

        符号说明：

S(t)	易感人群	E(t)	潜伏人群
I(t)	感染人群	R(t)	免疫人群
β	单位时间内平均传播人数	N	地区总人口数
C	平均潜伏周期	D	平均传染周期

        建模如下：

             dS/dt = -(β*I(t))*(S(t)/N)           (易感人数的变化)

             dE/dt = β*I(t)*S(t)/N-1/C*E(t)   (潜伏人数变化率 = 新增加潜伏感染人数-潜伏转确诊人数)

             dI/dt = 1/C*E(t)-1/D*I(t)           (感染人数的变化 = 潜伏转确诊人数-治愈人数)

             dR/dt = 1/D*I(t)                        (康复者人数变化)

             N = S+E+I+R                            (总的人数限定)

       其中：（1）β/N 可以用λ替代，λ表示平均传染接触率

                   （2）1/C 可以用a来替代，a表示平均发病比例

                   （3）1/D 可以用μ来替代，μ表示平均治愈比例

       最终可简化模型为：

 dS/dt = -λSI     S(0) = s0

 dE/dt = λSI-aE   E(0) = e0

 dI/dt = aE-μI    I(0) = i0

 dR/dt = μI

        经过网络以及文献资料可知，SEIR模型并没有解析解，只有数值解，所以可以尝试给与初值，来求得不同时间点的疫情发生情况。

二、传统模型求解与分析

        设该地区共有10000人，使用365天作为一个周期，单个体平均传播人数为3，潜伏周期为14天，传染周期为14天。

        使用python以及scipy、numpy、和matploylib库完成。具体实现代码如下：

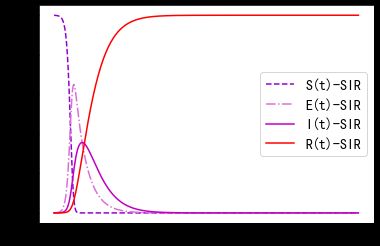
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
N = 10000
S_0 = 10000-1  #初始存在一个感染者，则剩下来的都是易感者
E_0 = 1   #初始存在1一个潜伏者
I_0 = 1     #初始存在感染者
R_0 = 0       #初值不存在康复者
#使用365天作为一个周期，单个体平均传播人数为3，潜伏周期为14天，传染周期为14天
t_max = 365
lamda = 3/10000 #λ平均传染接触率
aerf = 1/14#a平均每天发病比例
mu = 1/14 #μ平均每天治愈比例
def SIER(y,t):
    s = y[0]
    e = y[1]
    i = y[2]
    r = y[3]
    return  -lamda*s*i, lamda*s*i-aerf*e,aerf*e-mu*i,mu*i
t = np.linspace(0,365,t_max+1)#获得101个数据点
initial = (S_0,E_0,I_0,R_0)
ySEIR = odeint(SIER,initial,t)
print(ySEIR)
plt.plot(t, ySEIR[:,0], '--', color='darkviolet', label='S(t)-SIR')
plt.plot(t, ySEIR[:,1], '-.', color='orchid', label='E(t)-SIR')
plt.plot(t, ySEIR[:,2], '-', color='m', label='I(t)-SIR')
plt.plot(t, ySEIR[:,3],  color='r', label='R(t)-SIR')
plt.legend(loc = 'best')
plt.show()

        最终实现后的图像展示如下：

        从图中可知，在20天左右易感人群降为0，即所有人都经历或已经成为了潜伏者和感染者。潜伏者和感染者分别在30天以及40天左右来到了波峰值，随后也逐渐降为0。最终所有人在150天左右完成群体免疫。

三、改进模型求解与分析

        现如今保持社交距离成为一件人际交流活动比较关注的事情，并且全国各地的疫情仍然此起彼伏。所以探究保持社交距离对于疫情防控的重要性，是一件很有意义的事情。

对于SEIR模型方程的改进其实较为简单，即控制易感人群即可。改进公式如下：

         通过替换传统SEIR模型的前两项，即可达到设计控制的数学目的，假定社交距离的变化从1到10,1表示社交限制较少，10表示最高限制等级的社交距离控制。我们较为关注S(t)以及I(t)的变化，更改上方代码之后，输出对比图像如下：

 

        由图中可见，随着社交距离的扩大，易感人群单位时间的减少量相应减少，最终的停滞量相应增加；感染人群波峰到来的时间得到了有效延后，逐渐降低了波峰的大小。总的而言，从数学层面，社交距离的保持，能够有效促进了政府以及地区抗疫的成功性。

四、总结与感受

        对于传染病模型的研究，这只是初始，甚至说入门级别。随着之后更多数学元素的加入，模型只会愈加庞大和复杂。

        慢慢积累，慢慢长大吧。