连通分量(quick-union)

连通域问题的抽象表述是存在N个节点和M条边，被边直接或间接相连的所有节点共同形成一个域，称为连通域。在进行有限次的连接后，需要快速求出连通域的个数，或者判断任意两个节点的连通性。连通域的个数也称为连通分量，该算法也被称为Union-Find。

例如，下图中的节点就包含三个连通域（红，黑，蓝）。

把节点看作人，把边看作关系，那么连通域就可以用来抽象人群划分问题。把点看作触点，把边看作导线，这就是电路板布线问题。同样连通域也可以用来抽象网络连接问题，用来判断网络中节点的连通性。

在不同的场景下，节点有着不同的具体表示，但是做为算法，我们可以采用更抽象的形式，用0到N-1表示N个节点。我们很容易想到可以用一个数组来表示这N个节点，但是如何在一维数组上构造连接关系需要我们动一点脑筋。

一维数组的每个元素其实都包含着两个信息，一是下标，二是值。下标是固定不可变的信息，我们用它来表示节点，而值就可以用来构造连接关系。在接下来的描述中，我们会频繁使用"节点"和"下标"这两个表述，你需要知道它们是等价的。

连接的含义是通过一个节点可以找到另一个节点。如果我们在某个下标对应的值填入另一个下标，那么就相当于在这两个下标之间建立了一个单向连接。如下图所示，这就是我们需要的全部技巧。

此时判断两个节点是否相连就转换为判断两个下标对应的值是否相等。下标对应的值是什么呢？是另一个下标，或者我们可以称它为父节点。

这样的连接实际上构成了一颗自底向上的树，我们无法从根节点找到叶子节点，但是可以从任意一个节点找到根节点，如果两个节点的根节点相同，那么它们就位于同一颗树，也就是在同一个连通域。对于根节点，我们只需要将它的值设置成它自己的下标即可，也就是让根节点指向它自己。这样，凡是下标与值相等的就是根节点，不相等就是非根节点。当然，设置成一个特殊值，如-1也是可以的。

构建一颗自顶向下的树至少需要三个域，而构建一颗自底向上的树只需要两个域，因为一个节点可以有任意个子节点，但只能有一个父节点。

下面是一个四个节点的例子，我们依次连接(3,2)，(3,1)和(3,0)。

在开始之前我们需要先明确需要做什么，我们至少需要四个操作：

• 连接两个节点：Union
• 判断两个节点是否相连：Connected
• 计算连通域个数：Count
• 寻找一个节点的根节点：Find

每当我们新增一个有效连接时，都会将两个连通域合并成一个，这种二变一的结果就是相比于连接之前，连通域的个数会减少一个，而初始时，没有任何连接，有多少节点就有多少连通域。因此对于Count，我们可以记录初始连通域个数，然后在Union时更新它。就目前为止，我们至少可以写出下面的代码。

type UF struct {
  n    int
  node []int
}

func New(n int) (uf UF) {
  uf.n = n
  uf.node = make([]int, n)
  for i := 0; i < n; i++ {
    uf.node[i] = i
  }
  return
}

func (u UF) Count() int {
  return u.n
}

func (u UF) Connected(p, q int) bool {
  return u.Find(p) == u.Find(q)
}

func (u *UF) Union(p, q int) {
  if u.Connected(p, q) {
    return
  }
  //do union
  u.n--
}

func (u *UF) Find(p int) int {
  //find root of i
}

两个节点的连接是非常简单的，两个连通域的连接也不难，但是这里存在两种选择，不同的选择会带来不同的实现和性能表现。

连接两个连通域也就是合并两棵树，第一种方式是将一棵树的所有节点都挂到另一棵树的根节点上(如下图左)，第二种方式是只将根节点挂到另一棵树的根节点上(如下图右)。

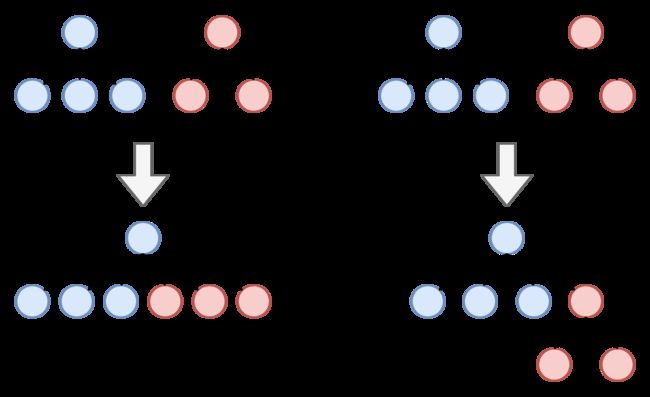
第一种方式产生的树只有两层，根节点和叶节点，它非常利于Find操作，但是不利于Union操作，因为Union时需要遍历一棵树。这里实际的操作是遍历数组，因为树只有两层，所以我们遍历数组一次就能找到全部节点。因此，第一种方式的实现也称为quick-find算法。以下是该算法的Union和Find的实现。

func (u *UF) Union(p, q int) {
  pRoot, qRoot := u.Find(p), u.Find(q)
  if pRoot == qRoot { //已连接
    return
  }
  //将连通域p合并到q
  for i := 0; i < len(u.node); i++ {
    if u.node[i] == pRoot {
      u.node[i] = qRoot
    }
  }

  u.n--
}

func (u *UF) Find(p int) int {
  return u.node[p] //因为此时的树只有两层
}

第二种方式会产生层次，使树长高。显然它是利于Union而不利于Find的，因为Union操作可以一次完成，但Find操作可能需要多次访问才能找到根节点，最坏的情况就是树变成单链表。这种方式也称为quick-union算法。以下是算法的Union和Find的实现。

func (u *UF) Union(p, q int) {
  pRoot, qRoot := u.Find(p), u.Find(q)
  if pRoot == qRoot { //已连接
    return
  }
  //将连通域p合并到q
  u.node[pRoot] = qRoot

  u.n--
}

func (u *UF) Find(p int) int {
  for p != u.node[p] {
    p = u.node[p]
  }
  return p
}

quick-union算法还有一个问题，就是它"欠扁"。树的高度是影响quick-union算法性能的关键，为了避免quick-union算法中最坏情况的出现，我们需要保证每次连接时都将小树连接到大树上。为此我们需要另一个数组来记录下以每个节点为根节点的树的大小。所以这种优化算法也叫加权quick-union算法，"权"就是一颗树的节点数。

首先我们需要对数据结构做一点小小的修改：

type UF struct {
  n    int
  node []int
  size []int //记录树大小
}

func New(n int) (uf UF) {
  uf.n = n
  uf.node = make([]int, n)
  uf.size = make([]int, n)
  for i := 0; i < n; i++ {
    uf.node[i] = i
    uf.size[i] = 1 //初始时只有一个节点
  }
  return
}

下面是加权quick-union算法的Union的实现。

func (u *UF) Union(p, q int) {
  pRoot, qRoot := u.Find(p), u.Find(q)
  if pRoot == qRoot { //已连接
    return
  }
  //将连通域p合并到q
  if u.size[pRoot] < u.size[qRoot] {
    u.node[pRoot] = qRoot
    u.size[qRoot] += u.size[pRoot]
  } else {
    u.node[qRoot] = pRoot
    u.size[pRoot] += u.size[qRoot]
  }

  u.n--
}

还能不能让树再扁平一点呢？

最扁平的树是quick-find算法的树，但是Union的成本太高，没关系，一招乾坤大挪移将它的成本转嫁给Find就好了。在Find操作时，我们增加一个操作，如果当前节点的父节点不是根节点，那么就让该节点指向它的祖父节点。这样Union可以和加权quick-uion算法一样，我们将原本在Union中做的扁平化延迟到了Find中。虽然不能像quick-find一样扁，但是至少比加权quick-uion扁了不少。下面是该算法的Find的实现。

func (u *UF) Find(p int) int {
  for p != u.node[p] {
    u.node[p] = u.node[u.node[p]] //提升p节点的位置
    p = u.node[p]
  }
  return p
}

至此，连通域问题的原理和优化就已经全部介绍完了。在连通域算法中，我们只知道两个节点相连，但是不知道它们如何相连。因为我们在构造树的过程中丢掉了"如何相连"的信息，这也导致了连接无法删除。