MATLAB数值计算学习笔记（二）误差理论和非线性方程求解

一.误差理论

误差来源

1.模型误差
2.观测误差
3.截断误差：求解模型所用数值方法为近似方法因此有误差存在。
4.舍入误差

误差基本概念

绝对误差

给定一实数$x^{\ast }$,其近似值为$x$，则称$e=x^{\ast }-x$为近似值$x$的绝对误差,若存在一个正实数\varepsilon，使得$$|e|=|x^{\ast }-x|\le \epsilon$$则称其为近似值的绝对误差限.

相对误差

相对误差公式：$$e_r=\frac{x^{\ast }-x}{x^{\ast }}$$
实用相对误差公式：$$\overline{e_r}=\frac{x^{\ast }-x}{x}$$

有效数字

误差传播

函数运算中误差的传播可以用函数的泰勒展开式进行估计：
$$f(x^{\ast })-f(x)=f^{\prime }(x)(x^{\ast }-x)+\frac{1}{2}{f}^{\prime \prime }(\xi ){(x^{\ast }-x)}^2$$
$$|f(x^{\ast })-f(x)|\le |f^{\prime }(x)|e(x)+\frac{1}{2}|f^{\prime \prime }(\xi )|{(e(x))}^2$$
忽略$e(x)$的高阶项，其误差限为：
$$\epsilon (f(x))\approx |f^{\prime }(x)|e(x)$$
其解的相对误差是：
$$\overline{{\epsilon }_r}(f(x))\approx |f\prime (x)|\frac{e(x)}{f(x)}$$
相对误差限为：
$${\epsilon }_r(f(x))=|f\prime (x)|\frac{e(x)}{f(x)}$$

应注意的问题

为了减小舍入误差的影响：
1.避免两个详尽的数相减
2.避免绝对值过小的数作除数
3.避免大数吃掉小数
4先化简再计算
5.采用数值稳定性好的算法

MATLAB数值计算精度

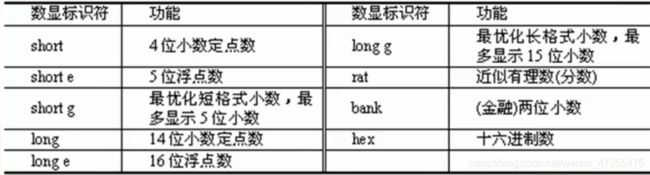
数据显示格式

控制数据输出格式的指令是format
format 数显标识符

运算精度

MATLAB提供了三种运算精度的算法：
数值算法：每个数值都取16位有效数字，运算速度最快。
符号算法：每个数据均为符号，精确但是慢，占用内存多。
可控精度算法：利用控制精度指令digits（n）使运算以n位有效数字进行，亦可用vpa（）函数

举例

秦九韶算法

function y=QJS(fun,x)
fun=sym(fun);
a=sym2poly(fun);
s(1)=a(1);
for k=2:length(a)
    s(k)=s(k-1)*x+a(k);
end
y=s(end);

二. 非线性方程（组）求解

二分法

优点：简单，对f（x）要求不高，连续即可
缺点：无法求复根和偶重根，收敛慢

function [x,fx,iter,X] =bisect(fun,a,b,eps,varargin)
%二分法
%二分法求非线性方程的根
%输入参数：
%——fun：待求根方程的函数
%——a，b：初始区间的端点
%——eps：精度要求，默认值为1e-6
%——p1,p2,...：求根函数附加参数
%输出参数：
%——x:非线性方程组的近似根
%——fx:根x处的函数值
%——iter：迭代次数
%——X：每一步迭代的结果
if nargin<3
    error('输入参数至少需要3个!');
end
if nargin<4
    isepmty(eps);eps=1e-6;
end
fa=feval(fun,a,varargin{:});
fb=feval(fun,b,varargin{:});
k=1;
if fa*fb>0
    warning(['区间[',num2str(a),',',num2str(b),']可能没有根'])
elseif fa==0
    x=a;fx=fa;
elseif fb==0
    x=b;fx=fb;
else
    while abs(b-a)>eps
        x=(a+b)/2;
        fx=feval(fun,a,varargin{:});
        if fa*fx>0
            a=x;
            fa=fx;
        elseif fb*fx>0
            b=x;
            fb=fx;
        else
            break
        end
        X(k)=x;k=k+1;
    end       
end
iter=k;

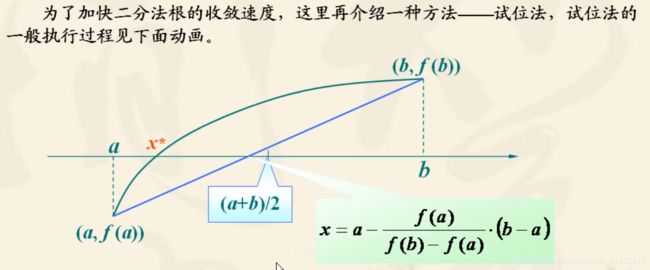
试位法

function [x,fx,iter,X] =test_bit(fun,a,b,eps,varargin)
%试位法求非线性方程的根
%输入参数：
%——fun：待求根方程的函数
%——a，b：初始区间的端点
%——eps：精度要求，默认值为1e-6
%——p1,p2,...：求根函数附加参数
%输出参数：
%——x:非线性方程组的近似根
%——fx:根x处的函数值
%——iter：迭代次数
%——X：每一步迭代的结果
if nargin<3
    error('输入参数至少需要3个!');
end
if nargin<4
    isepmty(eps);
    eps=1e-6;
end
fa=feval(fun,a,varargin{:});
fb=feval(fun,b,varargin{:});
k=1;
if fa*fb>0
    warning(['区间[',num2str(a),',',num2str(b),']可能没有根'])
elseif fa==0
    x=a;fx=fa;
elseif fb==0
    x=b;fx=fb;
else
    while abs(b-a)>eps%控制试位法结束条件
        x=b-(b-a)/(fa-fb)*fb;
        fx=feval(fun,x,varargin{:});%计算x处的函数值
        if fa*fx>0%条件
            a=x;%端点更新
            fa=fx;%端点函数值更新
        elseif fb*fx>0%条件
            b=x;%端点更新
            fb=fx;%端点函数值更新
        else
            break
        end
        X(k)=x;k=k+1;
    end       
end
iter=k;

简单迭代法

function [x,iter,X] = fixpt(g,x0,eps,maxiter)
%简单迭代法求非线性方程的根
%输入参数：
%——g：迭代函数
%——x0：初始迭代点
%——eps：精度要求，默认值为1e-6
%——maxiter：最大迭代次数，默认1e4
%输出参数：
%——x:非线性方程组的近似根
%——iter：迭代次数
%——X：每一步迭代的结果
if nargin<2
    error('输入参数至少需要3个');
end
if nargin<3
    isempty(eps);
    eps=1e-6;
end
if nargin<4
    isempty(maxiter);
    maxiter=1e4;
end
err=1;k=0;
while err>eps
    k=k+1;
    x1=feval(g,x0);
    err=abs(x1-x0);
    x0=x1;
    X(k)=x1;
end
if k==maxiter
    error('迭代次数超限')
end
x=x1;iter=k;X=X';
end 

收敛才可以迭代出结果

牛顿法

 function [x,iter,X] = newton(fun,x0,eps,maxiter)
%牛顿法求非线性方程的根
%输入参数：
%——fun：迭代函数
%——x0：初始迭代点
%——eps：精度要求，默认值为1e-6
%——maxiter：最大迭代次数，默认1e4
%输出参数：
%——x:非线性方程组的近似根
%——iter：迭代次数
%——X：每一步迭代的结果
if nargin<2
    error('输入参数至少需要3个');
end
if nargin<3
    isempty(eps);
    eps=1e-6;
end
if nargin<4
    isempty(maxiter);
    maxiter=1e4;
end
err=1;k=0;
while err>eps
    k=k+1;
    [fx0,dfx0]=feval(fun,x0);
    if dfx0==0
        error('f（x）在x0处的导数为0，停止计算')
    end
    x1=x0-fx0/dfx0;
    err=abs(x1-x0);
    x0=x1;
    X(k)=x1;
end
if k>=maxiter
    error('迭代次数超限')
end
x=x1;iter=k;X=X';
end

牛顿下山法

function [x,iter,X] = newton_down(fun,x0,eps,maxiter)
%牛顿下山法求非线性方程的根
%输入参数：
%——fun：迭代函数
%——x0：初始迭代点
%——eps：精度要求，默认值为1e-6
%——maxiter：最大迭代次数，默认1e4
%输出参数：
%——x:非线性方程组的近似根
%——iter：迭代次数
%——X：每一步迭代的结果
if nargin<2
    error('输入参数至少需要3个');
end
if nargin<3
    isempty(eps);
    eps=1e-6;
end
if nargin<4
    isempty(maxiter);
    maxiter=1e4;
end
[fx0,dfx0]=feval(fun,x0);
k=0;tol=fx0/dfx0;
while abs(tol)>eps
    lambda=1;
    [fx0,dfx0]=feval(fun,x0);
    x1=x0-lambda*fx0/dfx0;
    [fx1,dfx1]=feval(fun,x1);
    while abs(fx1)>=abs(fx0)%保证迭代后的函数值比之前小
        lambda=lambda/2;
        x1=x0-lambda*fx0/dfx0;%牛顿迭代下山
        [fx1,dfx1]=feval(fun,x1);
        x0=x1;
    end
    tol=fx1/dfx1;
    k=k+1;
    x0=x1;
    X(k)=x1;
end
if k>=maxiter
    error('迭代次数超限')
end
x=x1;iter=k;X=X';
end

割线法

function [x,iter,X] = secant(fun,x0,eps,maxiter)
%割线法求非线性方程的根
%输入参数：
%——fun：迭代函数
%——x0：初始迭代点
%——eps：精度要求，默认值为1e-6
%——maxiter：最大迭代次数，默认1e4
%输出参数：
%——x:非线性方程组的近似根
%——iter：迭代次数
%——X：每一步迭代的结果
if nargin<2
    error('输入参数至少需要3个');
end
if nargin<3
    isempty(eps);
    eps=1e-6;
end
if nargin<4
    isempty(maxiter);
    maxiter=1e4;
end
f0=feval(fun,x0);%计算x0处的函数值
f1=feval(fun,x1);%计算x1处的函数值
k=0;
while err>eps
    k=k+1;
    x2=x1-f1*(x1-x0)/(f1-f0);
    f0=f1;
    x0=x1;x1=x2;
    f1=feval(fun,x1);%计算x1处的函数值
    X(k)=x1;
end
if k>=maxiter
    error('迭代次数超限')
end
x=x2;iter=k;X=X';
end

实例

求解humps函数在区间[0,2]的零点

x=0:0.01:2;
fun=@(x)1./((x-.3).^2+.01)+1./((x-.9).^2+.04)-6;%定义函数表达式
[x1,fx1]=bisect(fun,0,2,1e-10);%二分法求解
plot(x,humps(x),[0,2],[0,0],'k',x1,fx1,'k*')
text(1,40,['humps函数零点{\itx}^*=',num2str(x1)])
title('humps函数零点求解')