Python预测——多元线性回归

答辩结束了，把论文里有用的东西摘出来。

多元线性回归

多元线性回归模型：

其中 y 为要预测的变量，x 为影响 y 值的变量，b 为回归系数，计算方式为：

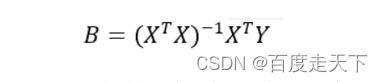
计算结果为一个矩阵，分别对应b0，b1，b2，b3。

实例

对猪肉价格进行预测，即猪肉价格作为 y，选择猪肉价格指数，生猪屠宰量，猪粮比作为相关变量，分别为x1，x2，x3。

数据收集

收集了从2020年5月至2022年2月的相关数据，其中price为猪肉价格，index为猪肉价格指数，作x1，kill为生猪屠宰量，作x2，rate为猪粮比，作x3，录入 excel 中，保存为 csv 文件。

代码

import pandas as pd   # 读数据库
import numpy as np    # 矩阵计算库

# 数据处理
def read_check_data():
    data_before = pd.read_csv(r"E:\python\django_p2\PIG_DATA.csv", encoding='gbk')

    total = data_before.isnull().sum().sort_values(ascending=False)
    print("total")
    print(total)
    # 表中若有空值，则舍弃
    data = data_before.drop(data_before[data_before['kill'].isnull()].index)
    x_first = np.array(data['index'])
    x_second = np.array(data['kill'])
    x_third = np.array(data['rate'])
    y_income = np.array(data['price'])
    return x_first, x_second, x_third, y_income


# 多元线性回归
def multiple_regression(x_first, x_second, x_third, y_income):
    x = range(1, len(x_first) + 1)
    print("矩阵：",list(zip(np.ones(len(y_income)), x_first, x_second, x_third)))
    Y = y_income.T                      # 矩阵
    X = np.array([list(x) for x in zip(np.ones(len(y_income)), x_first, x_second, x_third)])
    B = np.matmul(np.matmul(np.linalg.inv(np.matmul(X.T, X)), X.T), Y)   # (X.T * X)-1 * X.T * Y
    print("B = ", B)
    # 多元线性回归模型
    print("回归方程为 y = %f + %fx1 + %fx2 + %fx3" % (B[0], B[1], B[2], B[3]))
    y_predict = B[0] + B[1] * x_first + B[2] * x_second + B[3] * x_third
    return X, B, y_predict

检验

通过计算可决系数进行多元线性回归方程的拟合优度检验，可决系数是用来反映回归模式可靠程度的一个统计指标，可决系数越大，说明模型的预测值和观测值越接近，模型的拟合优度越好。计算方法如下：

# 检验
def check(y_real, y_predict, X, B):
    y1 = np.sum((y_predict - np.mean(y_real)) ** 2)
    y2 = np.sum((y_real - np.mean(y_real)) ** 2)
    R1 = y1 / y2
    print("可决系数R^2=", R1)

结果

if __name__ == '__main__':
    x_first, x_second, x_third, y_income = read_check_data()
    X, B, y_predict = multiple_regression(x_first, x_second, x_third, y_income)
    check(y_income, y_predict, X, B)

运行结果如下：

最终计算的可决系数约为0.93，说明猪肉价格与价格指数、屠宰量、猪粮比应该存在较高的相关性，且该回归模型的拟合度较高。

通过 excel 计算观察

发现有4组数据预测结果与实际结果相差较大，除此之外，平均误差值为1.13。
结果还可以，如果增加更多的相关变量和数据，误差应该会更小，但数据太太太太太难找了！！！！

本次数据来源

国家统计局
中华人民共和国农业农村部
全国重点农产品市场信息平台
全国农产品批发市场价格信息系统