Python实现多元线性回归算法预测房价

一、多元线性回归

社会经济现象的变化往往受到多个因素的影响，因此，一般要进行多元回归分析，我们把包括两个或两个以上自变量的回归称为多元线性回归 。
多元线性回归的基本原理和基本计算过程与一元线性回归相同，但由于自变量个数多，计算相当麻烦，一般在实际中应用时都要借助统计软件。这里只介绍多元线性回归的一些基本问题。
但由于各个自变量的单位可能不一样，比如说一个消费水平的关系式中，工资水平、受教育程度、职业、地区、家庭负担等等因素都会影响到消费水平，而这些影响因素（自变量）的单位显然是不同的，因此自变量前系数的大小并不能说明该因素的重要程度，更简单地来说，同样工资收入，如果用元为单位就比用百元为单位所得的回归系数要小，但是工资水平对消费的影响程度并没有变，所以得想办法将各个自变量化到统一的单位上来。前面学到的标准分就有这个功能，具体到这里来说，就是将所有变量包括因变量都先转化为标准分，再进行线性回归，此时得到的回归系数就能反映对应自变量的重要程度。这时的回归方程称为标准回归方程，回归系数称为标准回归系数，表示如下：

由于都化成了标准分，所以就不再有常数项 a 了，因为各自变量都取平均水平时，因变量也应该取平均水平，而平均水平正好对应标准分 0 ，当等式两端的变量都取 0 时，常数项也就为 0 了。
多元线性回归与一元线性回归类似，可以用最小二乘法估计模型参数，也需对模型及模型参数进行统计检验 。
选择合适的自变量是正确进行多元回归预测的前提之一，多元回归模型自变量的选择可以利用变量之间的相关矩阵来解决。

二、使用excel预估房价

1、打开数据集文件并删除非数据项，方便进行多元线性回归

2、选择回归数据分析

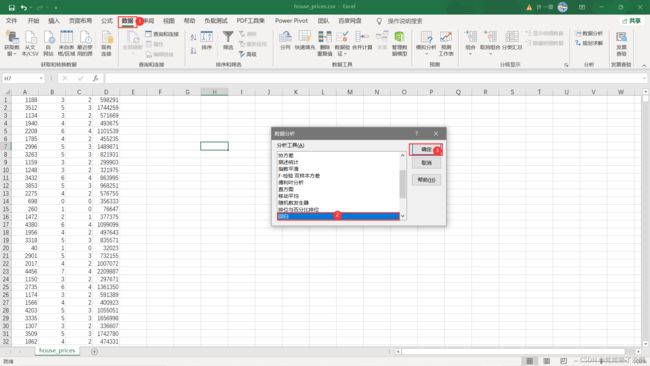
3、选择数据集，导出结果

4、结果

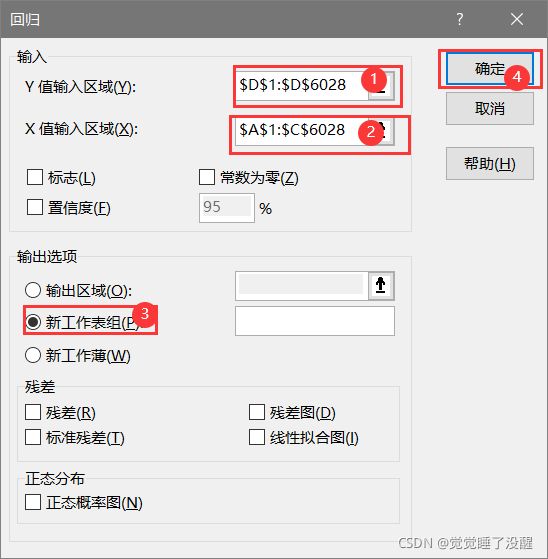
三、python实现预估房价（借助sklearn库）

1、上传数据集到jupyter

2、导入文件包

import pandas as pd
import numpy as np
import seaborn as sns
from sklearn import datasets
from sklearn.linear_model import LinearRegression
from statsmodels.formula.api import ols

3、读取数据集数据

df = pd.read_csv('house_prices.csv')
df.info()#显示列名和数据类型类型
df.head(6)#显示前n行，n默认为5

4、取出数据

#取出自变量
data_x=df[['area','bedrooms','bathrooms']]
data_y=df['price']

5、进行多元线性回归并得出结果

# 进行多元线性回归
model=LinearRegression()
l_model=model.fit(data_x,data_y)
print('参数权重')
print(model.coef_)
print('模型截距')
print(model.intercept_)

结果：

• 进行数据处理
  1、异常值检测

# 异常值处理
# ================ 异常值检验函数：iqr & z分数 两种方法 =========================
def outlier_test(data, column, method=None, z=2):
    """ 以某列为依据，使用 上下截断点法 检测异常值(索引) """
    """ 
    full_data: 完整数据
    column: full_data 中的指定行，格式 'x' 带引号
    return 可选; outlier: 异常值数据框 
    upper: 上截断点;  lower: 下截断点
    method：检验异常值的方法（可选, 默认的 None 为上下截断点法），
            选 Z 方法时，Z 默认为 2
    """
    # ================== 上下截断点法检验异常值 ==============================
    if method == None:
        print(f'以 {column} 列为依据，使用 上下截断点法(iqr) 检测异常值...')
        print('=' * 70)
        # 四分位点；这里调用函数会存在异常
        column_iqr = np.quantile(data[column], 0.75) - np.quantile(data[column], 0.25)
        # 1，3 分位数
        (q1, q3) = np.quantile(data[column], 0.25), np.quantile(data[column], 0.75)
        # 计算上下截断点
        upper, lower = (q3 + 1.5 * column_iqr), (q1 - 1.5 * column_iqr)
        # 检测异常值
        outlier = data[(data[column] <= lower) | (data[column] >= upper)]
        print(f'第一分位数: {q1}, 第三分位数：{q3}, 四分位极差：{column_iqr}')
        print(f"上截断点：{upper}, 下截断点：{lower}")
        return outlier, upper, lower
    # ===================== Z 分数检验异常值 ==========================
    if method == 'z':
        """ 以某列为依据，传入数据与希望分段的 z 分数点，返回异常值索引与所在数据框 """
        """ 
        params
        data: 完整数据
        column: 指定的检测列
        z: Z分位数, 默认为2，根据 z分数-正态曲线表，可知取左右两端的 2%，
           根据您 z 分数的正负设置。也可以任意更改，知道任意顶端百分比的数据集合
        """
        print(f'以 {column} 列为依据，使用 Z 分数法，z 分位数取 {z} 来检测异常值...')
        print('=' * 70)
        # 计算两个 Z 分数的数值点
        mean, std = np.mean(data[column]), np.std(data[column])
        upper, lower = (mean + z * std), (mean - z * std)
        print(f"取 {z} 个 Z分数：大于 {upper} 或小于 {lower} 的即可被视为异常值。")
        print('=' * 70)
        # 检测异常值
        outlier = data[(data[column] <= lower) | (data[column] >= upper)]
        return outlier, upper, lower

2、得到异常集并丢弃

outlier, upper, lower = outlier_test(data=df, column='price', method='z')#获得异常数据
outlier.info(); outlier.sample(5)
df.drop(index=outlier.index, inplace=True)#丢弃异常数据

3、取出变量

#取出自变量
data_x=df[['area','bedrooms','bathrooms']]
data_y=df['price']

4、进行多元线性回归并得到结果

# 进行多元线性回归
model=LinearRegression()
l_model=model.fit(data_x,data_y)
print('参数权重')
print(model.coef_)
print('模型截距')
print(model.intercept_)

结果：

三、基于统计分析库statsmodels进行线性回归

1、不使用虚拟变量
前面已经导入了statsmodels库我们做需要的包，这里直接开始编写

#不使用虚拟变量
lm = ols('price ~ area + bedrooms + bathrooms', data=df).fit()
lm.summary()

结果：

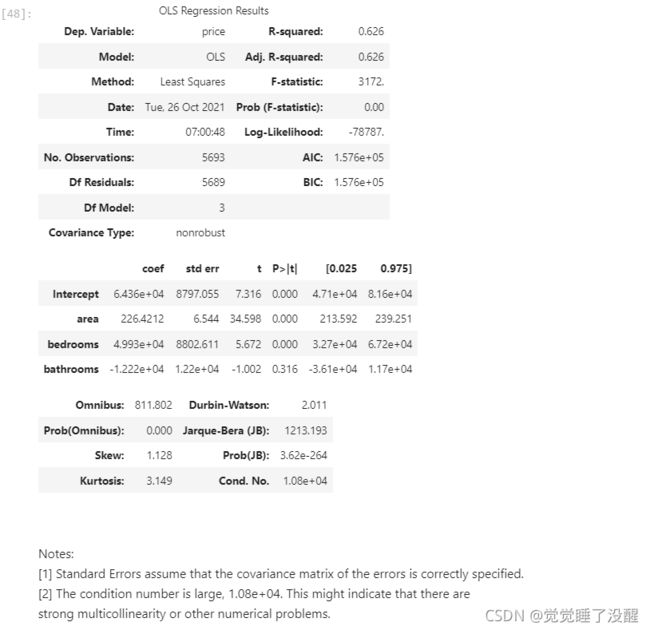
可以看到，不设置虚拟变量，这里的这里的相关系数R只有0.626，为了提升相关系数，我们需要设置虚拟变量。
2、设置虚拟变量再进行线性回归

# 设置虚拟变量
# 以名义变量 neighborhood 街区为例
nominal_data = df['neighborhood']

# 设置虚拟变量
dummies = pd.get_dummies(nominal_data)
dummies.sample()  # pandas 会自动帮你命名

# 每个名义变量生成的虚拟变量中，需要各丢弃一个，这里以丢弃C为例
dummies.drop(columns=['C'], inplace=True)
dummies.sample()
# 将结果与原数据集拼接
results = pd.concat(objs=[df, dummies], axis='columns')  # 按照列来合并
results.sample(3)
# 对名义变量 style 的处理可自行尝试
# 再次建模
lm = ols('price ~ area + bedrooms + bathrooms + A + B', data=results).fit()
lm.summary()

结果：

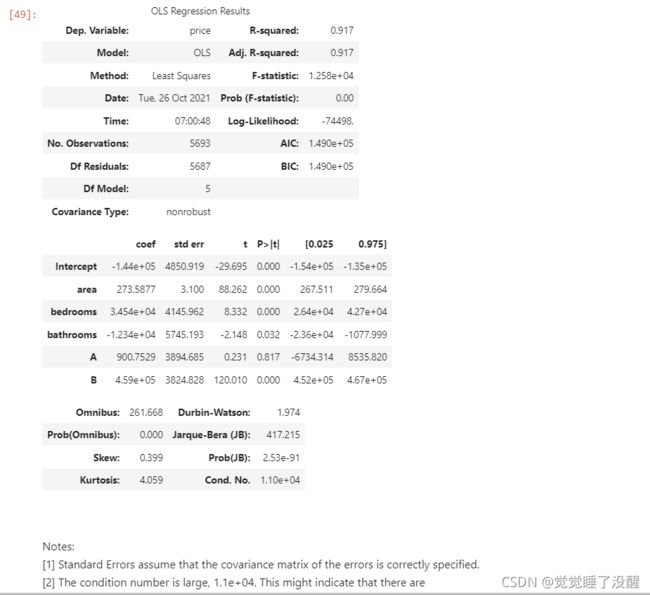
可以看到相关系数提升到了0.917，但是下面的note中提醒可能存在多元共线性，所以需要检测一下
3、检测多元共线性因子

# 自定义方差膨胀因子的检测公式
def vif(df, col_i):
    """
    df: 整份数据
    col_i：被检测的列名
    """
    cols = list(df.columns)
    cols.remove(col_i)
    cols_noti = cols
    formula = col_i + '~' + '+'.join(cols_noti)
    r2 = ols(formula, df).fit().rsquared
    return 1. / (1. - r2)
    test_data = results[['area', 'bedrooms', 'bathrooms', 'A', 'B']]
for i in test_data.columns:
    print(i, '\t', vif(df=test_data, col_i=i))

结果：

可以看到bedroom和bathroom相关程度较高
4、消除多元共线性，再进行线性回归

# 发现 bedrooms 和 bathrooms 存在强相关性，可能这两个变量是解释同一个问题
# 果然，bedrooms 和 bathrooms 这两个变量的方差膨胀因子较高，
 # 也印证了方差膨胀因子大多成对出现的原则，这里我们丢弃膨胀因子较大的 bedrooms 即可
lm = ols(formula='price ~ area + bathrooms + A + B', data=results).fit()
lm.summary()

结果：

可以看到R的值降低了0.01

四、结果分析

当不进行数据处理的时候用excel得到的结果和使用Python编程得到的结果是一样的，但是进行了数据清理之后得到的结果就变得很不一样了，而消除了共线性之后也使结果变得更加可靠了。

五、参考资料

jupyter多元线性回归算法预测房价
多元线性回归分析
多元线性回归算法