A星算法优化（四）贝塞尔曲线平滑处理

本文接上一篇：A星算法优化（三）搜索邻域

B站视频讲解：https://www.bilibili.com/video/BV1jS4y1K7qG?spm_id_from=333.999.0.0

如果有帮助，请三连支持，创作不易，禁止白嫖谢谢~

将从以下5个点进行改进：
1、启发函数——曼哈顿距离等
2、权重系数——动态加权等
3、搜索邻域——基于8邻域搜索改进
4、搜索策略——双向搜索、JPS策略等
5、路径平滑处理——贝塞尔曲线、B样条曲线等
实现效果

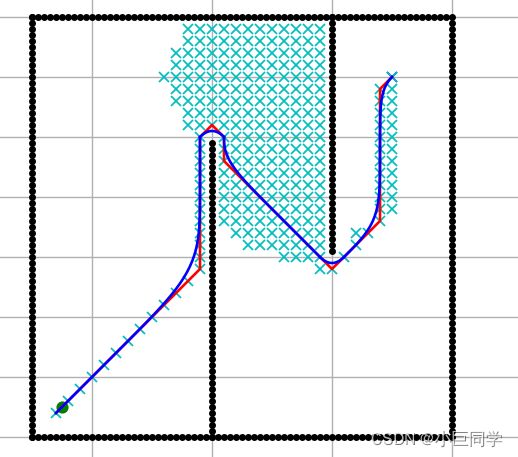
贝塞尔曲线

三步走：
1、先了解贝塞尔曲线原理
2、用代码实现
3、将代码应用在A星算法上

1、原理详细参考：https://www.aiuai.cn/aifarm1570.html
2、三阶贝塞尔曲线

任意数量控制点贝塞尔曲线python实现

#!/usr/bin/python3
#!--*-- coding: utf-8 --*--
import numpy as np 
import matplotlib.pyplot as plt 
from math import factorial

def comb(n, k):
    return factorial(n) // (factorial(k) * factorial(n-k))

def get_bezier_curve(points):
    n = len(points) - 1
    return lambda t: sum(comb(n, i)*t**i * (1-t)**(n-i)*points[i] for i in range(n+1))

def evaluate_bezier(points, total):
    bezier = get_bezier_curve(points)
    new_points = np.array([bezier(t) for t in np.linspace(0, 1, total)])
    return new_points[:, 0], new_points[:, 1]

points = np.array([[0, 0], [-1, 3], [4, 3], [6, 0], [7, 2.5]])
x, y = points[:, 0], points[:, 1]
bx, by = evaluate_bezier(points, 50)
# 
plt.plot(bx, by, 'b-')
plt.plot(x, y, 'r.')
plt.show()

5个控制点的运行结果如图：

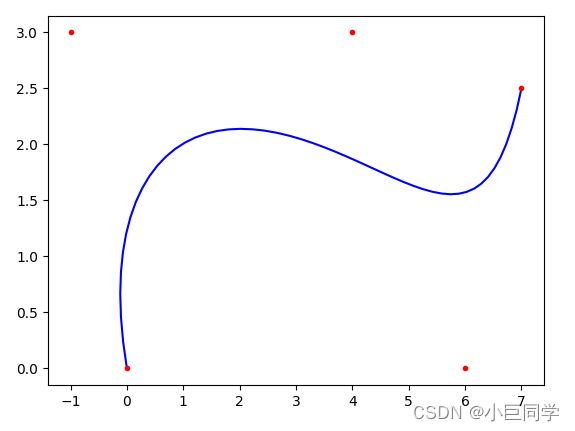
3、将代码应用在A星算法上
关键在于修改贝塞尔曲线的控制点，我们将A星算法最终运行得到的pathx，pathy两个列表中的值作为控制点，作为points

但要根据实际路径来选控制点，所以会分成好几段
最终平滑处理路径效果如下：

关键代码

 # 贝塞尔曲线的控制点，为了方便更改，可根据出图效果调整
    points = np.array([[pathx[0], pathy[0]], [pathx[1], pathy[1]], [pathx[2], pathy[2]],
                       [pathx[3], pathy[3]], [pathx[4], pathy[4]], [pathx[5], pathy[5]],
                       [pathx[6], pathy[6]], [pathx[7], pathy[7]], [pathx[8], pathy[8]],
                       [pathx[9], pathy[9]], [pathx[10], pathy[10]], [pathx[11], pathy[11]],
                       [pathx[12], pathy[12]], [pathx[13], pathy[13]], [pathx[14], pathy[14]],
                       [pathx[15], pathy[15]]])
    points1 = np.array([[pathx[15], pathy[15]], [pathx[16], pathy[16]], [pathx[17], pathy[17]]])
    points2 = np.array([[pathx[17], pathy[17]], [pathx[18], pathy[18]], [pathx[19], pathy[19]],
                        [pathx[20], pathy[20]], [pathx[21], pathy[21]], [pathx[22], pathy[22]],
                        [pathx[23], pathy[23]], [pathx[24], pathy[24]], [pathx[25], pathy[25]],
                        [pathx[26], pathy[26]], [pathx[27], pathy[27]]])
    points3 = np.array([[pathx[27], pathy[27]], [pathx[28], pathy[28]], [pathx[29], pathy[29]]])
    points4 = np.array([[pathx[29], pathy[29]], [pathx[30], pathy[30]], [pathx[31], pathy[31]],
                        [pathx[32], pathy[32]], [pathx[33], pathy[33]], [pathx[34], pathy[34]],
                        [pathx[35], pathy[35]], [pathx[36], pathy[36]], [pathx[37], pathy[37]],
                        [pathx[38], pathy[38]], [pathx[39], pathy[39]], [pathx[40], pathy[40]],
                        [pathx[41], pathy[41]], [pathx[42], pathy[42]], [pathx[43], pathy[43]],
                        [pathx[44], pathy[44]], [pathx[45], pathy[45]], [pathx[46], pathy[46]],
                        [pathx[47], pathy[47]], [pathx[48], pathy[48]], [pathx[49], pathy[49]],
                        [pathx[50], pathy[50]], [pathx[51], pathy[51]], [pathx[52], pathy[52]]])

    bx, by = evaluate_bezier(points, 50)
    bx1, by1 = evaluate_bezier(points1, 50)
    bx2, by2 = evaluate_bezier(points2, 50)
    bx3, by3 = evaluate_bezier(points3, 50)
    bx4, by4 = evaluate_bezier(points4, 50)

    if show_animation:
        plt.plot(pathx, pathy, "-r")  # 红色直线 最终路径
        plt.plot(bx, by, 'b-')  # 蓝色直线 贝塞尔曲线
        plt.plot(bx1, by1, 'b-')
        plt.plot(bx2, by2, 'b-')
        plt.plot(bx3, by3, 'b-')
        plt.plot(bx4, by4, 'b-')

        plt.show()
        plt.pause(0.001)  # 动态显示

参考：https://www.aiuai.cn/aifarm1570.html