数学建模——减肥模型Python实现
注:本模型代码在Jupyter编译
一、模型分析
通常,当体内能量守恒被破坏时就会引起体重的变化。人们通过饮食吸收热量,转化为脂肪等,导致体重增加:又由于代谢和运动消耗热量,引起体重减少。只要作适当的简化假设就可得到体重变化的关系。减肥计划应以不伤害身体为前提,这可以用吸收热量不要过少、减少体重不要过快来表达。当然,增加运动量是加速减肥的有效手段,也要在模型中加以考虑。
每日膳食中,营养的供给是作为保证正常人身体健康而提出的膳食质量标准,营养素的要求量是指维持身体正常的生理能所需的营养素的数量,如果人们在饮食中摄入营养素的数量低于这个数量,将使身体产生不利的影响。(每天膳食提供的热量不少于5000一7500J这是维持正常命活动的最少热量)
通常,制定减肥计划以周为时间单位比较方便,所以这里用离散时间模型——差分方程模型来谈论。
二、模型假设
根据上述分析,参考有关生理数据,作出以下简化假设:
- 体重增加正比于吸收的热量,平均每8000kcal增加体重1kg(kcal为非国际单位制单位1kca=4.2kj);
- 正常代谢引起的体重减少正比于体重,每周每公斤体重消耗热量一般在200kcal至320kcal之间,且因人而异,这相当于体重70kg的人每天消耗2000kcak至3200kcal;
- 运动引起的体重减少正比于体重,且与运动形式有关;
- 为了安全与健康,每周体重减少不宜超过1.5kg,每周吸收热量不要小于10000kcal。
三、符号说明
w0:初始体重
c0:初始每周摄入能量
a:1/8000(kg/kcal),体重增加正比于吸收的热量——每8000kcal增加体重1kg
b:代谢消耗系数(因人而异)
cmin:每周最少摄入的能量
h:每周运动时间
sport_type:运动类型
n:第一阶段吸收热量至下限时每周减少的热量
w_ideal:理想体重
四、代码实现
1.导入相关库并设置字体
from sympy import *
import numpy as np
import pandas as pd
%matplotlib inline
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False2.定义减肥计划的函数
def lose_weight(w0,c0,a,cmin,h,sport_type,n,w_ideal):
#计算代谢系数
w = w0
b = symbols('b')
eqb = Eq(w,w0+a*c0-b*w0)
b = solve(eqb,b)
b = b[0]
print('您的消耗系数b={}'.format(round(b,6)))
T = 35
w = np.zeros([T])
c = np.zeros([T])
t = np.zeros([T])
w[0] = w0
c[0] = c0
#第一阶段减肥计划
def T1(b,n,a,cmin):
t1 = 0
for k in range(T):
w[k+1] = w[k]-n
c[k+1] = (w[k+1]-w[k]+b*w[k])/a
t[k] = k
if c[k+1]>cmin:
t1 += 1
else:
break
return(t1)
t1 = T1(b,n,a,cmin)
print('您第一阶段减肥到热量吸收下限所需要的时间{}周'.format(t1))
#第二阶段减肥计划
w1 = w0 - n*t1
def T2(sport_type,n,t1,h,cmin,w1,w_ideal):
sport = {'run':7*h*a, 'dance':3*h*a, 'table':4.4*h*a, 'bicycle':2.5*h*a, 'non':0}
s = sport[sport_type] #运动代谢系数
w[0] = w0
t2 = 1
for k in range(t1+1,T):
w[k+1] = w[k] + a*cmin -(b+s)*w[k]
c[k] = cmin
t[k] = k
if w[k]五、调用函数及其结果
调用函数1:体重100kg,目前每周吸收20000kcal热量,现欲减肥至75kg,每周最少吸收10000kal,每周不运动。
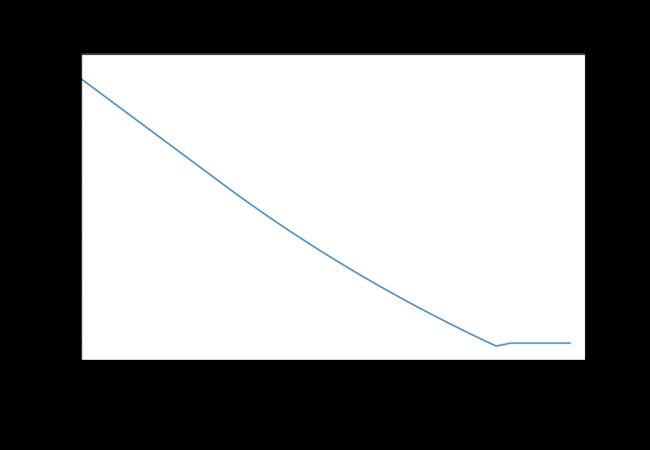
lose_weight(w0=100,c0=20000,a=1/8000,cmin=10000,h=0,sport_type='non',n=1,w_ideal=75)调用结果:
您的消耗系数b=0.025000
您第一阶段减肥到热量吸收下限所需要的时间10周
您第二阶段减肥到目标体重所需要的时间19周
您达到目标体重后,每周需要吸收热量15000cal可以使体重维持75kg不变
您两阶段减肥到理想体重所需要的时间为:29周
week weight intake caloric
0 0.0 100.000000 20000.0
1 1.0 99.000000 12000.0
2 2.0 98.000000 11800.0
3 3.0 97.000000 11600.0
4 4.0 96.000000 11400.0
5 5.0 95.000000 11200.0
6 6.0 94.000000 11000.0
7 7.0 93.000000 10800.0
8 8.0 92.000000 10600.0
9 9.0 91.000000 10400.0
10 10.0 90.000000 10200.0
11 11.0 89.000000 10000.0
12 12.0 88.025000 10000.0
13 13.0 87.074375 10000.0
14 14.0 86.147516 10000.0
15 15.0 85.243828 10000.0
16 16.0 84.362732 10000.0
17 17.0 83.503664 10000.0
18 18.0 82.666072 10000.0
19 19.0 81.849420 10000.0
20 20.0 81.053185 10000.0
21 21.0 80.276855 10000.0
22 22.0 79.519934 10000.0
23 23.0 78.781935 10000.0
24 24.0 78.062387 10000.0
25 25.0 77.360827 10000.0
26 26.0 76.676807 10000.0
27 27.0 76.009887 10000.0
28 28.0 75.359639 10000.0
29 29.0 74.725648 10000.0
30 30.0 75.000000 15000.0
31 31.0 75.000000 15000.0
32 32.0 75.000000 15000.0
33 33.0 75.000000 15000.0
34 34.0 75.000000 15000.0调用函数2:体重100kg,目前每周吸收20000kcal热量,现欲减肥至75kg,每周最少吸收10000kal,每周跳舞10小时。
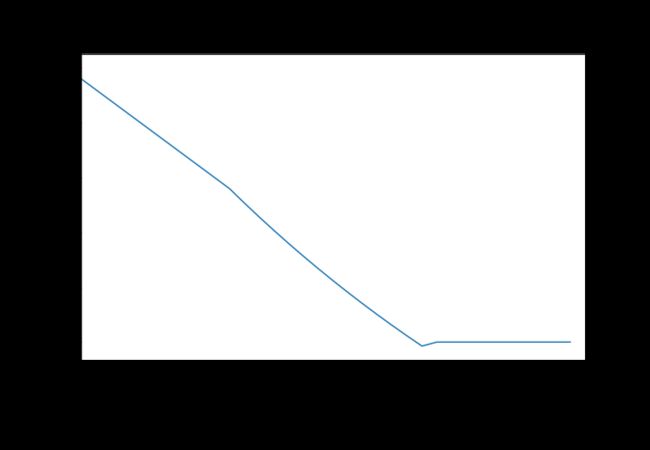
lose_weight(w0=100,c0=20000,a=1/8000,cmin=10000,h=10,sport_type='dance',n=1,w_ideal=75)调用结果:
您的消耗系数b=0.025000
您第一阶段减肥到热量吸收下限所需要的时间10周
您第二阶段减肥到目标体重所需要的时间14周
您达到目标体重后,每周需要吸收热量17250cal可以使体重维持75kg不变
您两阶段减肥到理想体重所需要的时间为:24周
week weight intake caloric
0 0.0 100.000000 20000.0
1 1.0 99.000000 12000.0
2 2.0 98.000000 11800.0
3 3.0 97.000000 11600.0
4 4.0 96.000000 11400.0
5 5.0 95.000000 11200.0
6 6.0 94.000000 11000.0
7 7.0 93.000000 10800.0
8 8.0 92.000000 10600.0
9 9.0 91.000000 10400.0
10 10.0 90.000000 10200.0
11 11.0 89.000000 10000.0
12 12.0 87.691250 10000.0
13 13.0 86.420127 10000.0
14 14.0 85.185548 10000.0
15 15.0 83.986463 10000.0
16 16.0 82.821853 10000.0
17 17.0 81.690724 10000.0
18 18.0 80.592116 10000.0
19 19.0 79.525093 10000.0
20 20.0 78.488746 10000.0
21 21.0 77.482195 10000.0
22 22.0 76.504582 10000.0
23 23.0 75.555075 10000.0
24 24.0 74.632867 10000.0
25 25.0 75.000000 17250.0
26 26.0 75.000000 17250.0
27 27.0 75.000000 17250.0
28 28.0 75.000000 17250.0
29 29.0 75.000000 17250.0
30 30.0 75.000000 17250.0
31 31.0 75.000000 17250.0
32 32.0 75.000000 17250.0
33 33.0 75.000000 17250.0
34 34.0 75.000000 17250.0