“张量网络压缩感知(TNCS)与无监督机器学习”学习笔记
TNCS学习笔记
- 一、前情小故事
- 二、张量网络压缩感知(TNCS)
-
- 如何构造和优化 ∣ ψ ⟩ \left| \psi \right\rangle ∣ψ⟩
- 如何通过在 ∣ ψ ⟩ \left| \psi \right\rangle ∣ψ⟩上的投影 ∣ Φ ⟩ \left| \Phi \right\rangle ∣Φ⟩还原信息
- 三、利用RO/VO/EOSP提高效率
-
- 随机排序(RO)
- 方差排序(VO)
- 纠缠有序抽样协议(EOSP)
这个笔记学习冉仕举老师等发表的"张量网络压缩感知与无监督机器学习"(Tensor network compressed sensing with unsupervised machine learning)等张量网络相关的内容。这个笔记是本人看论文的一些摘抄和个人理解,其目的为加深理解,方便回顾。 同时希望能用我自己的理解串联有关内容,站在不同的角度给大家展示不一样的理解。
我是一只正在不断学习、希望早日成为小白的小小白,有什么错误欢迎大家批评指正,喜欢的请点个赞哦!
一、前情小故事
在2120年七夕的前一周,主人公Bob和Alice在西大的操场上手牵着手散着步。“亲爱的,下周就到七夕了,你想要什么礼物?”,Bob一脸深情地望着Alice问道。Alice沉思了一会,心里嘀咕道:这都2120年了,作为一个刚学习了一定量子知识的学生,要学以致用,就用我所学的量子知识来回答!于是,Alice对Bob说:“我会把我想要的放在一张图片上,但是我不会把图片完整的告诉你,我只会告诉你图片一些像素的信息,然后你可以用25教那台名叫Born的机器去近似还原。给个小提示,这和我们之前学过的知识有关哦!”对于我们,当然是即将学的知识啦,小故事讲完,下面就正式进入正篇内容。
二、张量网络压缩感知(TNCS)
压缩感知是传统的通过采样压缩数据的一种强大的方案,当数据的采样困难或昂贵时,它特别有用。在量子通信中,由于量子态难以制备,测量也很困难,而且每一次测量都会在一定程度上坍缩或干扰量子态。最近,TN迅速发展成为一个强大的受量子启发的机器学习计算工具,为处理真实数据(如图像和文本)带来了新的可能性和广阔的前景,在基于多量子位或多体态的全量子过程中,至少在这些量子过程的经典模拟中已经证明了高效率。
张量网络压缩感知(TNCS)主要思想是通过在状态 ∣ ψ ⟩ \left| \psi \right\rangle ∣ψ⟩下实现对信息进行编码和通信,也被称为Born机器,是由无监督TN机器学习算法训练的。
Alice想要向Bob发送一条经典信息 { x } \left\{ {{x}} \right\} {x},例如,由100个像素组成的裙子的图像。她只打算通过经典通信向Bob发送 { x s e n t } \left\{ {{x}^{sent}} \right\} {xsent}表示的少量像素,这些信息是公开的。其余的信息 { x r e s t } \left\{ {{x}^{rest}} \right\} {xrest}将被编码到Born机器中。要恢复 { x r e s t } \left\{ {{x}^{rest}} \right\} {xrest},Bob将 { x s e n t } \left\{ {{x}^{sent}} \right\} {xsent}投射到 ∣ ψ ⟩ \left| \psi \right\rangle ∣ψ⟩上,得到另一个纠缠状态 ∣ Φ ⟩ \left| \Phi \right\rangle ∣Φ⟩,并且 { x r e s t } \left\{ {{x}^{rest}} \right\} {xrest}将被编码到距离 ∣ Φ ⟩ \left| \Phi \right\rangle ∣Φ⟩最小的可分离状态中。因此,Bob可以通过在 ∣ ψ ⟩ \left| \psi \right\rangle ∣ψ⟩上实现投影可靠地恢复 { x r e s t } \left\{ {{x}^{rest}} \right\} {xrest},或者在TN机器学习方面通过对 ∣ Φ ⟩ \left| \Phi \right\rangle ∣Φ⟩抽样产生 { x r e s t } \left\{ {{x}^{rest}} \right\} {xrest}。
看了上面不知道在看的你有没有一种我好像知道了些什么又好像什么也不知道。
如何构造和优化 ∣ ψ ⟩ \left| \psi \right\rangle ∣ψ⟩
假设Alice想要发送给Bob一幅由TNCS绘制的手写数字 “3” 的图像。她首先利用MNIST中许多由 “3” 组成的图片训练集训练 ∣ ψ ⟩ \left| \psi \right\rangle ∣ψ⟩作为生成模型,这可以通过无监督TN机器学习算法来完成。首先将像素映射到量子态,例如第n个像素被映射到一个量子态:
x n → ∣ s ( x n ) ⟩ = cos ( x n π / 2 ) ∣ 0 ⟩ + sin ( x n π / 2 ) ∣ 1 ⟩ x_{n} \rightarrow\left|s\left(x_{n}\right)\right\rangle=\cos \left(x_{n} \pi / 2\right)|0\rangle+\sin \left(x_{n} \pi / 2\right)|1\rangle xn→∣s(xn)⟩=cos(xnπ/2)∣0⟩+sin(xnπ/2)∣1⟩
其中 0 < x n < 1 0<{{x}_{n}}<1 0<xn<1 , ∣ 0 ⟩ \left| 0 \right\rangle ∣0⟩和 ∣ 1 ⟩ \left| 1 \right\rangle ∣1⟩是泡利矩阵 σ ^ z {{\hat{\sigma }}^{z}} σ^z的两个特征态。这样,一个带有像素 { x } \left\{ {{x}} \right\} {x} = ( x 1 {{x}_{1}} x1, x 2 {{x}_{2}} x2,…)的图像被映射到一个可分离状态
∣ ψ ⟩ = ∏ n ∣ s ( x n ) ⟩ |\psi\rangle=\prod_{n}\left|s\left(x_{n}\right)\right\rangle ∣ψ⟩=n∏∣s(xn)⟩
然后对Born机器 ∣ ψ ⟩ \left| \psi \right\rangle ∣ψ⟩进行优化。
相信经过前面的学习,绝大多数的小伙伴对于像素映射到量子态 ∣ s ( x n ) ⟩ \left|s\left(x_{n}\right)\right\rangle ∣s(xn)⟩和图像映射到量态 ∣ ψ ⟩ \left| \psi \right\rangle ∣ψ⟩是没什么问题的。但是可能会对 ∣ ψ ⟩ \left| \psi \right\rangle ∣ψ⟩的优化感到很困惑。以下是我看了论文之后的个人理解,如果有错误请帮我指出来,谢谢!
优化 ∣ ψ ⟩ \left| \psi \right\rangle ∣ψ⟩的步骤:
(1)随机初始化 ∣ ϕ i ⟩ = ∏ n ∣ s ( x i , n ) ⟩ \left|\phi_{i}\right\rangle=\prod_{n}\left|s\left(x_{i, n}\right)\right\rangle ∣ϕi⟩=∏n∣s(xi,n)⟩,也就是随机抽取一张图像进行映射作为初始化的 ∣ ϕ i ⟩ \left|\phi_{i}\right\rangle ∣ϕi⟩;
(2)利用TT分解将初始化的 ∣ ϕ i ⟩ \left|\phi_{i}\right\rangle ∣ϕi⟩分解为满足MPS态的张量网络,用它作为初始 ∣ ψ ⟩ \left| \psi \right\rangle ∣ψ⟩,为了避免指数墙的问题,需要分解的同时进行裁剪;
(3)定义交叉损失函数,通过梯度更新方法,更新张量网络中的张量,使得损失函数降到极低,具体操作过程上篇博客有涉及,可以戳这个链接监督/非监督张量网络机器学习;
(4)通过对张量网络中的张量进行更新,最后的得到的 ∣ ψ ⟩ \left| \psi \right\rangle ∣ψ⟩就是优化后的 ∣ ψ ⟩ \left| \psi \right\rangle ∣ψ⟩。
如何通过在 ∣ ψ ⟩ \left| \psi \right\rangle ∣ψ⟩上的投影 ∣ Φ ⟩ \left| \Phi \right\rangle ∣Φ⟩还原信息
当我们把Born机器 ∣ ψ ⟩ \left| \psi \right\rangle ∣ψ⟩训练好之后该做什么呢?当然是利用它去还原我们原本的信息啦!按照上面Bob的做法,要恢复 { x r e s t } \left\{ {{x}^{rest}} \right\} {xrest},Bob将 { x s e n t } \left\{ {{x}^{sent}} \right\} {xsent}投射到 ∣ ψ ⟩ \left| \psi \right\rangle ∣ψ⟩上,得到另一个纠缠状态 ∣ Φ ⟩ \left| \Phi \right\rangle ∣Φ⟩
∣ Φ ⟩ = ∏ x n ∈ { x [ sent ] ] ⟨ s ( x n ) ∣ Ψ ⟩ / C |\Phi \rangle =\prod\limits_{{{x}_{n}}\in \{{{x}^{[\text{sent}]}}]}{\left\langle s\left( {{x}_{n}} \right)\mid \Psi \right\rangle }/C ∣Φ⟩=xn∈{x[sent]]∏⟨s(xn)∣Ψ⟩/C
其中,C是常数,需要标准化 ∣ Φ ⟩ |\Phi \rangle ∣Φ⟩, { x r e s t } \left\{ {{x}^{rest}} \right\} {xrest}将被编码到距离 ∣ Φ ⟩ \left| \Phi \right\rangle ∣Φ⟩最小的可分离状态中,具体步骤可以戳这希尔伯特空间、特征映射与量子概率。需要注意的是,其实我们一开始并不知道我们需要还原的信息是什么,也就是在这个公式:
P ( { x n [ B ] } ) = ∏ ⊗ n ⟨ x n [ B ] ∣ ρ ^ [ B ] ∣ x n [ B ] ⟩ \text{P}\left( \left\{ x_{n}^{[\text{B}]} \right\} \right)=\prod\limits_{\otimes n}{\left\langle x_{n}^{[\text{B}]}\left| {{{\hat{\rho }}}^{[B]}} \right|x_{n}^{[\text{B}]} \right\rangle } P({xn[B]})=⊗n∏⟨xn[B]∣∣∣ρ^[B]∣∣∣xn[B]⟩
我们并不知道 ⟨ x n [ B ] ∣ \left\langle x_{n}^{[\mathrm{B}]}\right| ⟨xn[B]∣∣∣,只是随机生成满足概率分布的 ⟨ x n [ B ] ∣ \left\langle x_{n}^{[\mathrm{B}]}\right| ⟨xn[B]∣∣∣,至于最后这个结果是否正确还需要在后面的数据集上测试以此来验证生成的是否有效。
机器学习的意义在于我们只使用训练集中的 “3” 图像来优化 ∣ ψ ⟩ \left| \psi \right\rangle ∣ψ⟩,预期 ∣ ψ ⟩ \left| \psi \right\rangle ∣ψ⟩ 给出任意 “3” 图像的概率分布。换句话说, ∣ ψ ⟩ \left| \psi \right\rangle ∣ψ⟩学习训练集中 “3” 图像的概率分布但是可以识别出任意 ∣ ψ ⟩ \left| \psi \right\rangle ∣ψ⟩没有学习过的 “3” 图像,这种机器学习模型处理训练集以外信息的能力被称为泛化能力。
三、利用RO/VO/EOSP提高效率
当前面的一系列的映射、Born机器 ∣ ψ ⟩ \left| \psi \right\rangle ∣ψ⟩的优化和信息的还原的操作已经大致了解之后,按照做科研需要精益求精的要求,当然要重新开始对我们的源头进行精简啦! { x s e n t } \left\{{{x}^{sent}} \right\} {xsent}应该被挑选以便于 { x s e n t } \left\{ {{x}^{sent}} \right\} {xsent}尽量小,与此同时Bob可以从 ∣ Φ ⟩ \left| \Phi \right\rangle ∣Φ⟩中准确地重建剩下的像素 { x r e s t } \left\{ {{x}^{rest}} \right\} {xrest}。
关于抽样,如果Alice选择不同的 { x s e n t } \left\{ {{x}^{sent}} \right\} {xsent},结果将会改变。这也是下面我们要进行讨论的所在。
随机排序(RO)
在标准压缩感知计划中,可以从图像中随机选择一定数量的像素作为 { x s e n t } \left\{ {{x}^{sent}} \right\} {xsent}。由于随机选择的像素近似导致平均分布的频率,同时图像在频率空间通常是稀疏的,因此可以压缩采样。对于TNCS,其中一个可以随机从 { x } \{x\} {x}选择 { x s e n t } \left\{ {{x}^{sent}} \right\} {xsent},这就是随机排序(RO)。在 { x s e n t } \left\{ {{x}^{sent}} \right\} {xsent}中包含足够的数据, ∣ Φ ⟩ |\Phi \rangle ∣Φ⟩最终会投射到这样一种状态
∣ Φ ⟩ = ∏ n ∣ s ( x n ) ⟩ ( x n ∈ { x rest } ) |\Phi \rangle=\prod_{n}\left|s\left(x_{n}\right)\right\rangle\left(x_{n} \in\left\{x^{\text {rest }}\right\}\right) ∣Φ⟩=n∏∣s(xn)⟩(xn∈{xrest })
这是所有独立态中离 ∣ Φ ⟩ |\Phi \rangle ∣Φ⟩最近的独立态,因此,Bob可以通过简单的在 ∣ Φ ⟩ |\Phi \rangle ∣Φ⟩上投影来访问 { x r e s t } \left\{ {{x}^{rest}} \right\} {xrest}。
到目前为止,如果
∏ x n ∈ { x [ r e s t ] ] ∣ ⟨ Φ ∣ s ( x n ) ⟩ ∣ → 1 {{\prod }_{{{x}_{n}}\in \{{{x}^{[rest]}}]}}\left| \left\langle \Phi \mid s\left( {{x}_{n}} \right) \right\rangle \right|\to 1 ∏xn∈{x[rest]]∣⟨Φ∣s(xn)⟩∣→1
并且
# { x s e n t } ≪ # { x } \#\left\{x^{\mathrm{sent}}\right\} \ll \#\{x\} #{xsent}≪#{x}
我们可以看到数据被TNCS有效地压缩,换句话说,Bob将准确地得到 { x s e n t } \left\{ {{x}^{sent}} \right\} {xsent}当 ∣ Φ ⟩ |\Phi \rangle ∣Φ⟩映射到一个足够接近可分离状态 { x r e s t } \left\{ {{x}^{rest}} \right\} {xrest}的状态。
分别用RO和MNIST和fashion-MNIST资料的测量方法对TNCS进行了测试,每个数据集包含10类图像,总共有6万张训练图像和1万张测试图像。每幅图像包含28×28 = 784个灰度像素。下图展示了不同压缩比下的TNCS的精确度 r r r= N f / N {{N}_{f}}/N Nf/N,其中 N f {N}_{f} Nf是 { x s e n t } \left\{ {{x}^{sent}} \right\} {xsent}的数量, N N N 是 { x } \left\{ {{x}} \right\} {x}的数量。精度由平均峰值信噪比(PSNR)来表征:
PSNR ( { x } , { y } ) = 10 log 10 784 ∑ n ( x n − y n ) 2 \operatorname{PSNR}(\{x\},\{y\})=10 \log _{10} \frac{784}{\sum_{n}\left(x_{n}-y_{n}\right)^{2}} PSNR({x},{y})=10log10∑n(xn−yn)2784
其中,{x}表示原始数据,{y}表示重建数据。取MPS键维度分别为16和40,一般来说,PSNR会随着 r r r 和 χ \chi χ的增加而增加,而TNCS通过简单地从 { x } \left\{ {{x}} \right\} {x}中随机取样作为 { x s e n t } \left\{ {{x}^{sent}} \right\} {xsent},对 ∣ ψ ⟩ \left| \psi \right\rangle ∣ψ⟩进行一次投影就能很好地工作。
方差排序(VO)
除了RO之外,还有一种自然选择方法称为方差排序(VO),即根据方差选择像素点。第n个像素的方差是从训练集计算出来的:
V n = ∑ i [ x i , n − ( ∑ j x j , n / K ) ] 2 / K V_{n}=\sum_{i}\left[x_{i, n}-\left(\sum_{j} x_{j, n} / K\right)\right]^{2} / K Vn=i∑[xi,n−(j∑xj,n/K)]2/K
其中 x i , n {{x}_{i,n}} xi,n 为训练集第 i i i 幅图像中的第 n n n 个像素,K 为训练图像的个数。选择 { x s e n t } \left\{ {{x}^{sent}} \right\} {xsent}作为方差最大的像素点,PSRN有明显的提高,如上图所示。
还有一种更合理的方法是根据纠缠态 ∣ ψ ⟩ \left| \psi \right\rangle ∣ψ⟩ 进行选择,使 { x s e n t } \left\{ {{x}^{sent}} \right\} {xsent}从Born机器给出的概率分布中最小化 { x r e s t } \left\{ {{x}^{rest}} \right\} {xrest}的不确定性。已知 { x s e n t } \left\{ {{x}^{sent}} \right\} {xsent},则满足 { x r e s t } \left\{ {{x}^{rest}} \right\} {xrest}的条件概率分布:
P ( { x [ rest ] } ∣ { x [ sent ] } ) = ∣ ∏ x n ∈ { x restl } ⟨ s ( x n ) ∣ Φ ⟩ ∣ 2 P\left(\left\{x^{[\text {rest }]}\right\} \mid\left\{x^{[\text {sent }]}\right\}\right)=\left|\prod_{x_{n} \in\left\{x^{\text {restl }}\right\}}\left\langle s\left(x_{n}\right) \mid \Phi\right\rangle\right|^{2} P({x[rest ]}∣{x[sent ]})=∣∣∣∣∣∣xn∈{xrestl }∏⟨s(xn)∣Φ⟩∣∣∣∣∣∣2
上式怎么得来的,需要看推导过程的小伙伴可以看这里张量网络图片生成与压缩
纠缠有序抽样协议(EOSP)
我们的任务是找到最小化纠缠熵的N个像素 { x s e n t } \left\{ {{x}^{sent}} \right\} {xsent}
S S h a n = − ∑ { x [rest] } P ( { x [rest ] } ∣ { x [ sent ] } ) ln P ( { x [rest ] } ∣ { x [ sent ] } ) S^{\mathrm{Shan}}=-\sum_{\left\{x^{\text {[rest] }}\right\}} P\left(\left\{x^{\text {[rest }]}\right\} \mid\left\{x^{[\text {sent }]}\right\}\right) \ln P\left(\left\{x^{\text {[rest }]}\right\} \mid\left\{x^{[\text {sent }]}\right\}\right) SShan=−{x[rest] }∑P({x[rest ]}∣{x[sent ]})lnP({x[rest ]}∣{x[sent ]})
针对这个任务,让我们从一个更简单的问题开始:如果Alice只发送一个像素,应该发送哪个像素? 这可以由单点纠缠熵来决定,被定义为
S n e n t = − Tr ρ ^ n ln ρ ^ n S_{n}^{\mathrm{ent}}=-\operatorname{Tr} \hat{\rho}_{n} \ln \hat{\rho}_{n} Snent=−Trρ^nlnρ^n
S n e n t = − Tr ρ ^ n ln ρ ^ n S_{n}^{\mathrm{ent}}=-\operatorname{Tr} \hat{\rho}_{n} \ln \hat{\rho}_{n} Snent=−Trρ^nlnρ^n将拥有除去第n个qubit系统剩余部分的信息。这样的数量被用来安全地减少像素的数量,从而实现高效的监督TN机器学习。
有了 S n e n t = − Tr ρ ^ n ln ρ ^ n S_{n}^{\mathrm{ent}}=-\operatorname{Tr} \hat{\rho}_{n} \ln \hat{\rho}_{n} Snent=−Trρ^nlnρ^n,Alice可以选择满足argmax S n e n t = − Tr ρ ^ n ln ρ ^ n S_{n}^{\mathrm{ent}}=-\operatorname{Tr} \hat{\rho}_{n} \ln \hat{\rho}_{n} Snent=−Trρ^nlnρ^n的像素,这样Bob就能从一个像素中获得尽可能多的信息。
基于上述方案,作者提出了以下选取 { x s e n t } \left\{ {{x}^{sent}} \right\} {xsent}的马尔可夫抽样策略,称为纠缠有序抽样协议(EOSP)。按照我个人的理解就是计算 ∣ Ψ ( N ) ⟩ |\Psi(N)\rangle ∣Ψ(N)⟩所有qubits的单点纠缠熵,选取满足argmax S n e n t = − Tr ρ ^ n ln ρ ^ n S_{n}^{\mathrm{ent}}=-\operatorname{Tr} \hat{\rho}_{n} \ln \hat{\rho}_{n} Snent=−Trρ^nlnρ^n的像素,记录这个像素的位置并把像素传给Bob。更新原来的张量网络 ∣ Ψ ( N − 1 ) ⟩ = ⟨ s n ~ ∣ Ψ ( N ) ⟩ / C |\Psi(N-1)\rangle=\left\langle s_{\tilde{n}} \mid \Psi(N)\right\rangle / C ∣Ψ(N−1)⟩=⟨sn~∣Ψ(N)⟩/C 。当 { x s e n t } \left\{ {{x}^{sent}} \right\} {xsent}足够还原信息的时候就可以停止传递满足argmax S n e n t = − Tr ρ ^ n ln ρ ^ n S_{n}^{\mathrm{ent}}=-\operatorname{Tr} \hat{\rho}_{n} \ln \hat{\rho}_{n} Snent=−Trρ^nlnρ^n的像素了,此时 ∣ Ψ ( N − N f ) ⟩ = ∣ Φ ⟩ \left|\Psi\left(N-N_{f}\right)\right\rangle=|\Phi\rangle ∣Ψ(N−Nf)⟩=∣Φ⟩
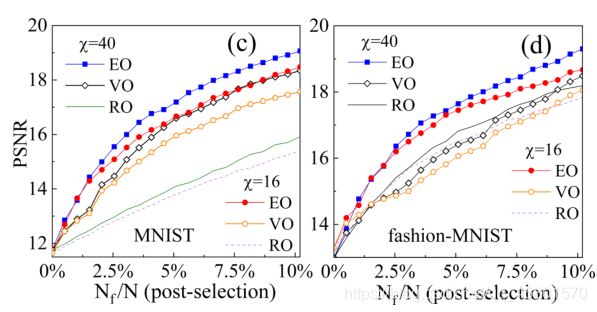
由图可以看到,三种选择方法EOSP、VO和RO的PSNR都得到了显著改善。
我是一只正在不断学习、希望早日成为小白的小小白,有什么错误欢迎大家批评指正,喜欢的请点个赞哦!



